Орієнтований граф

Орієнтований граф (коротко орграф) — (мульти)граф, ребрам якого присвоєно напрямок. Орієнтовані ребра називаються також дугами, а в деяких джерелах (Оре) і просто ребрами.
Основні поняття[ред. | ред. код]
Формально, орграф D = (V, E) є множина E впорядкованих пар вершин .
Дуга {u, v} інцидентна до вершин u і v. При цьому говорять, що u — початкова вершина дуги, а v — кінцева вершина.
Орграф, отриманий з простого графу орієнтацією ребер, називається орієнтованим. На відміну від останнього, у довільного простого орграфу дві вершини можуть з'єднуватися двома різноорієнтованими дугами.
Орієнтований повний граф називається турніром.
Зв'язність[ред. | ред. код]
Маршрутом орграфу називають послідовність вершин і дуг, виду (вершини можуть повторюватися). Довжина маршруту — кількість дуг у ньому.
Шлях — маршрут орграфу без повторюваних дуг, простий шлях — без повторюваних вершин. Якщо існує шлях з однієї вершини в іншу, то друга вершина досяжна з першої.
Контур — замкнений шлях.
Для напівмаршруту знімається обмеження на напрямок дуг, аналогічно визначаються напівшлях і напівконтур.
Орграф сильно зв'язний, або просто сильний, якщо всі його вершини взаємно досяжні; Односторонньо зв'язний, або просто односторонній якщо для будь-яких двох вершин, принаймні одна досяжна з іншою; Слабо зв'язний, або просто слабкий, якщо при ігноруванні напрямів дуг виходить зв'язний (мульти)граф;
Максимальний сильний підграф називається сильною компонентою; одностороння компонента і слабка компонента визначаються аналогічно .
Конденсацією орграфу D називають орграф D*, вершинами якого служать сильні компоненти D, а дуга в D* показує наявність хоча б однієї дуги між вершинами, що входять у відповідні компоненти.
Додаткові визначення[ред. | ред. код]
Орієнтований ациклічний граф або «гамак» є безконтурним орграфом.
Орієнтований граф, що отриманий із заданого зміною напрямку ребер на протилежні, називається зворотним.
Зображення і властивості всіх орграфів з трьома вузлами[ред. | ред. код]
Легенда: С — слабкий, ОС — односторонній, СС — сильний, Н — орієнтований граф, Г — гамак, Т — турніром.
| 0 дуг | 1 дуга | 2 дуги | 3 дуги | 4 дуги | 5 дуг | 6 дуг |
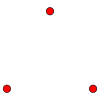 порожній, Н, Г порожній, Н, Г |
 Н, Г Н, Г |
 |
 ОС ОС |
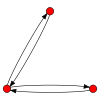 CC CC |
 CC CC |
 повний, CC повний, CC
|
|---|---|---|---|---|---|---|
 ОС, Н, Г ОС, Н, Г |
 CC, Н, Т CC, Н, Т |
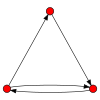 CC CC |
||||
 C, Н, Г C, Н, Г |
 ОС, Н, Г, Т ОС, Н, Г, Т |
 ОС ОС |
||||
 C, Н, Г C, Н, Г |
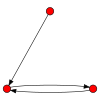 ОС ОС |
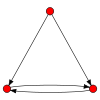 ОС ОС |
Застосування орграфів[ред. | ред. код]
Орграф широко застосовуються в програмуванні як спосіб опису систем зі складними зв'язками. Наприклад, одна з основних структур, що використовуються при розробці компіляторів і взагалі для подання комп'ютерних програм — граф потоків даних.
Бінарні відношення[ред. | ред. код]

Бінарне відношення над скінченним носієм може бути представлене у вигляді орграфу. Простим орграфом можна представити антирефлексивні відношення, в загальному випадку потрібен орграф з петлями. Якщо відношення симетричне, то його можна представити неорієнтованим графом, а якщо антисиметричне, то орієнтованим графом.
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
Література[ред. | ред. код]
- Харари Ф. Теория графов — М.: УРСС, 2003. — 300 с. — ISBN 5-354-00301-6.
- Оре, Ойстин Теория графов — М.: УРСС, 2008. — 352 с. — ISBN 978-5-397-00044-4.
- Альфред В. Ахо, Моника С. Лам, Рави Сети, Джеффри Д. Ульман Компиляторы: принципы, технологии и инструменты, 2 издание = Compilers: Principles, Techniques, and Tools — 2 изд. — М.: «Вильямс», 2008. — ISBN 978-5-8459-1349-4.

