Повний двочастковий граф

Повний двочастковий граф
Повний двочастковий граф із m = 5 та n = 3
Вершин	n + m
Ребер	mn
Радіус	$\left\{{\begin{array}{ll}1&m=1\vee n=1\\2&m\neq 1\wedge n\neq 1\end{array}}\right.$
Діаметр	$\left\{{\begin{array}{ll}1&m=n=1\\2&m\neq 1\wedge n\neq 1\end{array}}\right.$
Обхват	$\left\{{\begin{array}{ll}\infty &m=1\vee n=1\\4&m\neq 1\wedge n\neq 1\end{array}}\right.$
Автоморфізм	$\left\{{\begin{array}{ll}2m!n!&n=m\\m!n!&m\neq n\end{array}}\right.$
Хроматичне число	2
Хроматичний індекс	max{m, n}
Спектр	$\{0^{n+m-2},(\pm {\sqrt {nm}})^{1}\}$
Позначення	$K_{m,n}$

Повний двочастковий граф (бікліка) — спеціальний вид двочасткового графа, у якого будь-яка вершина першої частки з'єднана з усіма вершинами другої частки вершин.

Визначення

Повний двочастковий граф $G:=(V_{1}+V_{2},E)$ — це двочастковий граф, такий що для будь-яких двох вершин $v_{1}\in V_{1}$ і $v_{2}\in V_{2}$, $(v_{1},v_{2})$ є ребром в $G$. Повний двочастковий граф з частками розміру $|V_{1}|=m$ і $|V_{2}|=n$ позначається як. $K_{m,n}$.

Приклади

Графи-зірки $S_{3}$, $S_{4}$, $S_{5}$ і $S_{6}$.

Граф $K_{3,3}$.

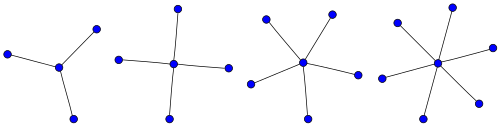
• Графи $K_{1,k}$ називаються зірками, всі повні двочасткові графи, які є деревами, є зірками.
• Граф $K_{1,3}$ називається клешнею та використовується для визначення графів без клешень.
• Граф $K_{3,3}$ іноді називається «комунальним графом», назва йде від класичної задачі «вода, газ та електрика», яка в сучасній інтерпретації використовує «комунальне» формулювання (підключити три будинки до водо- електро- та газопостачання без перетинів ліній на площині); задача нерозв'язна незважаючи на непланарність графа $K_{3,3}$.

Властивості

• Задача пошуку для даного двочасткового графа повного двочасткового підграфа $K_{m,n}$ NP-повна.
• Планарний граф не може містити $K_{3,3}$ як мінор графа. Зовніпланарний граф не може містити $K_{3,2}$ як мінор (Це недостатня умова планарності та зовнішньої планарності, а необхідна). І навпаки, будь-який непланарний граф містить або $K_{3,3}$, або повний граф $K_{5}$ як мінор (теорема Куратовського).
• Повні двочасткові графи $K_{n,n}$ є графами Мура і $(n,4)$-клітками.
• Повні двочасткові графи $K_{n,n}$ і $K_{n,n+1}$ є графами Турана.
• Повний двочастковий граф $K_{m,n}$ має розмір вершинного покриття, рівний $\min(m,n)$ і розмір реберного покриття, що дорівнює $\max(m,n)$.
• Повний двочастковий граф $K_{m,n}$ має максимальну незалежну множину розміром $\max(m,n)$.
• Матриця суміжності повного двочасткового графа $K_{m,n}$ має власні значення ${\sqrt {nm}}$, $-{\sqrt {nm}}$ і $0$ із кратностями $1$, $1$ і $n+m-2$ відповідно.
• Матриця Лапласа повного двочасткового графа $K_{m,n}$ має власні значення $n+m$, $n$, $m$, $0$ із кратностями $1$, $m-1$, $n-1$ і $1$ відповідно.
• Повний двочастковий граф $K_{m,n}$ має $m^{n-1}\cdot n^{m-1}$ кістякових дерев.
• Повний двочастковий граф $K_{m,n}$ має максимальне парування розміру $\min(m,n)$.
• Повний двочастковий граф $K_{n,n}$ має підхоже $n$-реберне розфарбування, яке відповідає латинському квадрату.

Останні два результати є наслідком теореми Холла, застосованої до $k$-регулярного двочасткового графа.

Див. також

• Вільний від біклік граф
• Двогранний граф
• Двочасткова розмірність
• Корона
• Цикл
• Шлях