Логістичне відображення
Логістичне відображення — точкове відображення, в якому в залежності від параметра проявляється широке коло синергетичних ефектів, таких як атрактори, граничні цикли, подвоєння періоду, детермінований хаос.
Логістичне відображення задається ітераційною формулою:
- ,
де n — крок, r — параметр. Початковою може бути будь-яка точка інтервалу (0,1). Параметр r може мати значення від 0 до 4.
Біфуркаційна діаграма[ред. | ред. код]
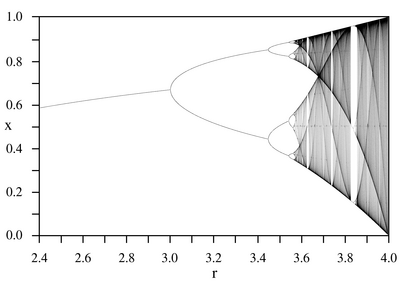

Біфуркаційна діаграма представлена на рисунку праворуч.
Область стабільності[ред. | ред. код]
В залежності від значення параметра r відображення має різну кількість нерухомих точок. При єдиною нерухомою точкою, яка визначається з рівняння
- ,
що лежить в інтервалі (0,1) є точка . Ця точка стійка, тому послідовність відображень збігається до нуля: при будь-якому значенні початкової точки .
При відображення має дві нерухомі точки: та . Перша з нерухомих точок є нестабільною, а друга стабільною, тому . Цей проміжок відзначений одною лінією на діаграмі.
Біфуркація утворення граничного циклу[ред. | ред. код]
При r > 3 число нерухомих точок не змінюється, але обидві нерухомі точки стають нестабільними. Оскільки відображення обмежене, то відсутність точкового атрактора означає утворення складнішого атрактора типу граничного циклу.
Хоча саме відображення не має стійких нерухомих точок, його квадрат такі стійкі нерухомі точки має. Ці точки визначаються з системи рівнянь:
Ця система рівнянь зводиться до одного рівняння, виключаючи змінну y
- .
Графік функції зображено на рисунку праворуч зеленою кривою. Вона має три нерухомі точки. Дві відмінні від нуля нерухомі точки задають граничний цикл. При відображенні першого порядку одна з них переходить у іншу, і навпаки. Тому на біфункаційній діаграмі в цій області одна лінія розгалужується на дві. Слово біфуркація означає розгалуження. Область граничного циклу існує при значеннях параметра .
Біфуркація подвоєння періоду[ред. | ред. код]
При значеннях параметра r, більших від , граничний цикл втрачає стійкість. При таких значення параметра стійкі нерухомі точки потрібно шукати у відображеннях вищих порядків. В певній області стійкі стаціонарні точки існують у відображення четвертого порядку. На графіку праворуч відповідна функція
зображена сірою кривою. У такого відображення існує чотири стаціонарні точки. Точка при послідовних ітераціях тепер буде почергово відвідувати околи вже не двох, а чотирьох точок. Граничний цикл ускладнюється, відбувається подвоєння його періоду від двох до 4-х.
Ситуація з періодом граничного циклу 4 існує в певній області параметра r, а потім змінюється — відбувається ще одне подвоєння періоду — до восьми, і так далі.
Детермінований хаос[ред. | ред. код]
При значеннях параметру r > 3,57 жоден із критичних циклів не має стабільності. З цього значення починається хаотична поведінка системи. Значення змінюється без періодичності. Таких хаос називається детермінованим, оскільки існує чіткий строго визначений закон, за яким можна визначити значення змінної на будь-якій ітерації, починаючи від вибраного початкового значення, однак в її поведінці немає періодичності. Якщо в області стійкості й граничних циклів поведінка відображень слабо залежала від початкової точки, то в області хаосу мала зміна початкового значення призводить до значної зміни значення n-тої ітерації.
В області хаосу існують несподівані вікна, коли при певних значеннях параметру поведінка відображення стає регулярною, наприклад, з'являються граничні цикли третього порядку.
Стала Фейгенбаума[ред. | ред. код]
Мітчел Фейгенбаум визначив рекурентну формулу, якій підпорядковані критичні значення параметра r, при яких відбуваються біфуркації періоду
- ,
де називається сталою Фейгенбаума.
Історія[ред. | ред. код]
Логістичне відображення популяризував у 1976 році біолог Роберт Мей. Фейгенбаум встановив значення своєї сталої дещо раніше в 1975 році, використовуючи кишеньковий калькулятор. Надалі він отримав її математично. В 1978 році він опублікував статтю, в якій показав, що схожі подвоєння періоду з відповідною універсальною константою відбуваються при переході до хаосу у широкому класі задач.
Див. також[ред. | ред. код]
| Ця стаття не містить посилань на джерела. (червень 2023) |


















