Множина великих тригонометричних сум

Множина великих тригонометричних сум — поняття теорії чисел — множина індексів, у яких перетворення Фур'є характеристичної функції заданої підмножини групи набуває досить великих значень.

Для зручності викладу далі у статті використовується скорочення МВТС, хоча воно не є загальноприйнятим.

Визначення

У класичному методі тригонометричних сум часто буває потрібно оцінити зверху значення модуля суми $\sum \limits _{x\in X}{e^{\frac {ax}{n}}}$ для деякої підмножини $X\subset {\mathbb {Z} }_{n}$ циклічної групи. Якщо ця сума має малий модуль за всіх $a\not \equiv 0{\pmod {n}}$, то з цього можна зробити висновки про рівномірність розподілу $X$ серед неперервних відрізків лишків за модулем $n$. Це виконується, наприклад, для множини квадратичних лишків (і взагалі степеневих лишків), дискретних логарифмів послідовних чисел або (для простих $n$) виразів вигляду $a+a^{-1}$, де $a^{-1}$ — обернений елемент ${\mathbb {F} }_{n}$ відносно множення (суми Клоостермана) .

Природно постає питання: якщо не для всіх $a\not \equiv 0{\pmod {n}}$ розглянуті суми мають малий модуль, то для скількох $a$ цей модуль може бути дуже великим, і для яких саме наборів значень $a$ це може виконуватись? Наприклад, очевидно, що якщо це виконується для $a$, то й для $-a$ теж, але виникає питання існування інших таких загальних закономірностей, які залежать від природи множини $X$.

Це питання широко розглянуто в адитивній комбінаториці, ідеєю якої і є виявлення закономірностей у структурі множин за мінімальних обмежень на них, а коефіцієнти Фур'є знаходять у ній широке застосування.

Визначення

Закономірності, що стосуються МВТС, розглядають, як правило, виходячи з двох параметрів — розміру основної множини та межі, за якою відокремлюють значення тригонометричних сум. Іноді для зручності межу на тригонометричні суми записують не в явному вигляді, а параметризують через її відношення до розміру множини (оскільки модуль суми, очевидно, ніколи не перевищує розміру множини). Через це, а також через відмінності нормування коефіцієнтів Фур'є, вирази у формулюваннях визначень і теорем у різних авторів можуть відрізнятися, але суть досліджуваних співвідношень залишається тією ж.

Нехай $N$ — натуральне число, $A\subset {\mathbb {Z} }_{N}$, $|A|=\delta N$ Нехай також ${\widehat {A}}(\xi )=\sum \limits _{x\in A}{e^{2\pi {\frac {\xi x}{N}}i}}$ означає $\xi$-й коефіцієнт Фур'є (не нормований) характеристичної функції $A$. Тоді множини великих тригонометричних сум з параметром визначаються (з точністю до параметра $\alpha$) як ${\mathcal {R}}_{\alpha }={\mathcal {R}}_{\alpha }(A)=\left\lbrace {\xi :|{\widehat {A}}(\xi )|\geq \alpha N}\right\rbrace$

Деякі прийоми вивчення

Наближення функції множиною

Для побудови прикладів множин, які мають МВТС з тими чи іншими властивостями, часто будують функції, які мають відповідні коефіцієнти Фур'є, а потім на цій підставі констатують існування множин, коефіцієнти Фур'є яких не сильно відрізняються від коефіцієнтів цих функцій. Підстави для цього дає така лема, доведення якої перегукується з загальною лінійно-алгебричною ідеєю і виходить за рамки науки про МВТС:

Якщо $f:{\mathbb {Z} }_{N}\to [0;1]$, то існує множина $S\subset {\mathbb {Z} }_{N}$ розміру $\left\lfloor {\sum \limits _{x}{f(x)}}\right\rfloor$ така, що $\forall r\in {\mathbb {Z} }_{N}:|{\widehat {S}}(r)-{\widehat {f}}(r)|\leq 20{\sqrt {N}}$

Зміна індикаторної функції при фільтруванні коефіцієнтів Фур'є за різними значеннями $\alpha$

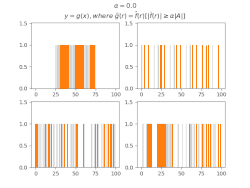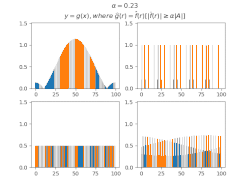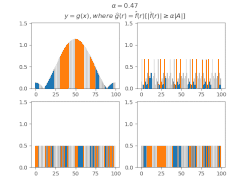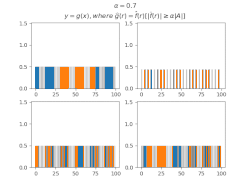
Фільтрування коефіцієнтів Фур'є

Для виведення загальних тверджень про МВТС деяких множин зручно використовувати функції, утворені з індикаторної функції множини фільтруванням коефіцієнтів Фур'є за цією МВТС, тобто таку функцію $f$, що

${\widehat {f}}(\xi )={\begin{cases}{\widehat {1_{A}}}(\xi )&\xi \in {\mathcal {R}}_{\alpha }(A)\\0&\xi \not \in {\mathcal {R}}_{\alpha }(A)\end{cases}}$

Виявляється, що в таких функцій більша частина суми значень також концентрується в $A$.

Властивості

Розмір

З рівності $\sum \limits _{\xi }{|{\widehat {A}}(\xi )|^{2}}=|A|^{2}$ легко виходить. що $|{\mathcal {R}}_{\alpha }|<{\frac {\delta }{\alpha ^{2}}}$.

Для деяких значень $\delta ,\alpha$ ця оцінка досить точна за порядком зростання.

Приклад — квадратичні лишки

Якщо $Q_{p}\subset {\mathbb {Z} }_{p}$ — множина квадратичних лишків за простим модулем $p$, $\delta ={\frac {p+1}{2p}},\ \alpha \approx {\frac {1}{2{\sqrt {p}}}}$, то для $|{\mathcal {R}}_{\alpha }(Q_{p})|=p$ оцінка перетворюється на нерівність близьку до $|{\mathcal {R}}_{\alpha }(Q_{p})|<2(p+1)$.

За допомогою конструкції вигляду $\bigcup \limits _{s=0}^{k-1}{(sp+Q_{p})}\subset {\mathbb {Z} }_{kp}$ цю ідею можна узагальнити на МВТС із меншою відносно модуля межею на значення суми. При цьому між оцінкою та реальним розміром МВТС утворюється та сама різниця.

Приклад — послідовні числа

У прикладі з квадратичними лишками величина $\delta ={\frac {p+1}{2p}}\approx {\frac {1}{2}}$ близька до фіксованої. Щоб знайти приклади із довільною величиною $\delta$, достатньо розглянути множину $A=\{1,2,\dots ,m\}\subset {\mathbb {Z} }_{N}$, де $m\ll N$.

Тоді $\forall \xi <{\frac {N}{4m}}\forall a\in A:\ \arg \left({e^{2\pi {\frac {\xi a}{N}}i}}\right)<{\frac {\pi }{2}}$ (тобто напрямки векторів, відповідних $e^{2\pi {\frac {\xi a}{N}}i}$, обмежені досить вузьким кутом) і тому $\forall \xi <{\frac {N}{4m}}:|{\widehat {A}}(\xi )|\gg {\frac {m}{2}}$, так що правильна оцінка знизу $|{\mathcal {R}}_{\frac {m}{2N}}(A)|\geq \left\lfloor {\frac {N}{4m}}\right\rfloor$. Більш того, оскільки $|{\widehat {A}}(\xi )|=|{\widehat {A}}(-\xi )|$, то правильно навіть, що $|{\mathcal {R}}_{\frac {m}{2N}}(A)|\geq \left\lfloor {\frac {N}{2m}}\right\rfloor$.

Однак при $\delta ={\frac {m}{N}},\ \alpha ={\frac {m}{2N}}$ оцінка зверху перетворюється на нерівність $|{\mathcal {R}}_{\alpha }(A)|\leq 4{\frac {N}{m}}$.

Виходить що $\left\lfloor {\frac {N}{2m}}\right\rfloor \leq |{\mathcal {R}}_{\alpha }(A)|\leq 4{\frac {N}{m}}$ та оцінка зверху також точна до множення на сталу.

Структура

Ступінь структурованості МВТС у різних сенсах можна оцінити досить точно, коли вони досить великі. У разі коли вони мають малий розмір, МВТС можуть бути цілком довільними.

Адитивна енергія

З одного боку, МВТС допускають нижню оцінку на адитивну енергію будь-якої своєї підмножини.

Якщо $B\subset {\mathcal {R}}_{\alpha }$, то $T_{k}(B)\gg _{k}{\frac {\alpha ^{2k}}{\delta ^{2k-1}}}|B|^{2k}$

Короткий опис ідеї доведення  

Достатньо в подібний спосіб оцінити енергію множини вигляду $B'\subset {\mathcal {R}}_{\alpha }\setminus {\mathcal {R}}_{2\alpha }$ і підсумувати результати за значеннями $\alpha ,2\alpha ,4\alpha ,\dots$

Для оцінки енергії $B'$ використовують функцію, коефіцієнти Фур'є якої є коефіцієнтами $1_{A}$, відфільтрованими за $B'$. Оскільки, із загальних міркувань, значення такої функції дуже насичені в $A$, то достатньо за допомогою серії нерівностей Гельдера та операцій зі згортками оцінити цю насиченість через побудову $\sum \limits _{u}{{{\Bigg \vert }{\sum \limits _{r}{{\widehat {f}}(r){\overline {{\widehat {f}}(r-u)}}}}{\Bigg \vert }}^{2}}$ і деякий множник, що залежить від $|A|$ (тобто, від $\delta$). Побудова ж $\sum \limits _{u}{{{\Bigg \vert }{\sum \limits _{r}{{\widehat {f}}(r){\overline {{\widehat {f}}(r-u)}}}}{\Bigg \vert }}^{2}}$, завдяки відніманню ${\mathcal {R}}_{2\alpha }$ з $B'$ (тобто, завдяки умові на оцінку ${\widehat {f}}(\xi )$ зверху), оцінюється зверху через величину адитивної енергії (з деяким додатковим множником).

З іншого боку, за деяких додаткових (не надто сильних) умов на параметри $k,\alpha ,\delta$ існує множина $A$, для якої правильна і верхня оцінка $T_{k}({\mathcal {R}}_{\alpha })\ll _{k}{\frac {\delta }{\alpha ^{2k}}}$, причому $|{\mathcal {R}}_{\alpha }|\gg {\frac {\delta }{\alpha ^{2}}}$. Це говорить про те, що іноді МВТС можуть бути все-таки досить великими та безструктурними одночасно.

Побудова

Для побудови використовують множину $\Lambda$, яка має особливим способом посилену властивість дисоціативності.

Саму множину $A$ визначають як об'єднання зсувів $|\Lambda |$ різних арифметичних прогресій із різницями $\lambda \in \Lambda$, причому зсуви вибирають так, щоб кожна нова прогресія, що додається до множини, мала з уже побудованою множиною якнайменший перетин.

МВТС такої множини містить об'єднання такої ж кількості інших арифметичних прогресій (що дозволяє говорити про її великий розмір) і водночас сама міститься в об'єднанні тих самих арифметичних прогресій, лише подовжених в обидва боки (а це дозволяє із загальних комбінаторних міркувань вивести, що її адитивна енергія не велика).

У випадку, коли ${\mathcal {R}}_{\alpha }$ має найбільший можливий розмір, ці оцінки (якщо першу розглядати для $B={\mathcal {R}}_{\alpha }$) збігаються з точністю до сталої, яка залежить від $k$. Тобто, для досить широкого класу значень параметрів $\delta ,\alpha$ існують множини, міра структурованості МВТС яких визначена майже однозначно, причому їхні МВТС виявляються тим більш безструктурними, чим більше в них елементів (чим більша різниця між $\delta$ і $\alpha$).

Адитивна розмірність

Інша досліджувана характеристика — адитивна розмірність МВТС, тобто розмір найбільшої дисоціативної множини, що міститься в ньому. Далі цю величину позначено як $\dim _{+}({\mathcal {R}}_{\alpha })$.

Чанг 2002 року довела, що $\dim _{+}({\mathcal {R}}_{\alpha })\ll {\left({\frac {\delta }{\alpha }}\right)}^{2}\log {\left({\frac {1}{\delta }}\right)}$. Основу доведення становило застосування нерівності Рудіна до функції, утвореної з індикаторної функції множини фільтруванням коефіцієнтів Фур'є ${\mathcal {R}}_{\alpha }$.

Разом з тим, Грін 2003 року показав, що за умов

• $\delta \leq {\frac {1}{8}}$

• $\alpha \leq {\frac {\delta }{32}}$

• ${\left({\frac {\delta }{\alpha }}\right)}^{2}\log {\left({\frac {1}{\delta }}\right)}\leq {\frac {\log N}{\log \log N}}$

існує множина $A$, для якої $\dim _{+}({\mathcal {R}}_{\alpha })\gg {\left({\frac {\delta }{\alpha }}\right)}^{2}\log {\left({\frac {1}{\delta }}\right)}$.

Тобто, розглядаючи досить великі значення сум, адитивну розмірність МВТС можна оцінити досить точно.

Довільність

Якщо МВТС досить мала, порівняно зі своїм найбільшим можливим розміром, то загальна оцінка на адитивну енергію виявляється тривіальною, тобто не дозволяє нічого сказати про внутрішню структуру множини.

Виявляється, що в цьому випадку про неї нічого сказати і не можна — тобто довільна множина може бути малою МВТС.

Теорема (Шкредов) Якщо $\delta <{\frac {1}{2}}$ $20{\frac {1}{\sqrt {N}}}<\alpha \leq {\frac {\delta }{2}}$ $|S|\leq {\frac {\delta }{2\alpha }}$ $S=-S$ то $\exists A:\ |A|=\left\lfloor {\delta N}\right\rfloor$ і ${\mathcal {R}}_{\alpha }(A)=S$

Короткий опис ідеї доведення  

Достатньо розглянути функцію $f$ таку, що

${\widehat {f}}(\xi )={\begin{cases}\delta &\xi =0\\2\alpha &\xi \in S\setminus \{0\}\\0&\xi \not \in S\end{cases}}$

і застосувати лему про наближення її коефіцієнтів Фур'є через коефіцієнти Фур'є індикаторної функції множини.

Основним обмеженням тут є $|S|\leq {\frac {\delta }{2\alpha }}$ — інші зумовлені загальною природою тригонометричних сум.

Обмеження на розмір можна ослабити до $|S|\leq {\frac {\delta }{\alpha }}\log {\frac {1}{\delta }}$, якщо додати умову на те, що $S$ має деяку властивість, яка є варіацією дисоціативності.

Зв'язок між МВТС різних множин

МВТС множин розміру $\left\lfloor {\frac {N}{2}}\right\rfloor$ (половина розміру групи) у певному сенсі покривають структуру решти МВТС.

Теорема (Грін) Якщо $\alpha \geq 80{\frac {1}{\sqrt {N}}}$, то для будь-якого $A\subset {\mathbb {Z} }_{N}$ існує $B\subset {\mathbb {Z} }_{N}$ таке, що $|B|=\left\lfloor {\frac {N}{2}}\right\rfloor$ і ${\mathcal {R}}_{\alpha }(A)\subset {\mathcal {R}}_{\frac {\alpha }{4}}(B)$

Узагальнення

МВТС можуть вивчатися не тільки для циклічних, але й для будь-яких груп, якщо правильно узагальнити поняття коефіцієнта Фур'є.

Наприклад, для будь-кого $\alpha <{\frac {1}{2}}$ та множини $A\subset {\mathbb {Z} }_{2}^{n}$ її $\alpha$-МВТС містить у собі підгрупу розміру ${}^{\left({\frac {1}{\alpha ^{3}}}\right)}2$ (останній вираз означає тетрацію).

Застосування

Чанг застосувала оцінки на адитивну розмірність МВТС для поліпшення оцінок у теоремі Фреймана.

Література

• Б. И. Сегал. Тригонометрические суммы и некоторые их применения к теории чисел // Успехи математических наук. — 1946. — Вып. 3—4 (13-14) (21 апреля). — С. 147—193.
• М. А. Королёв. Методы оценок коротких сумм Клоостермана // Чебышевский сборник. — 2016. — Т. 17, вып. 4 (21 апреля). — С. 79—109.
• И. Д. Шкредов. Некоторые примеры множеств больших тригонометрических сумм // Математический сборник. — 2007. — Т. 198, вып. 12 (21 апреля). — С. 105—140.
• И. Д. Шкредов. О множествах больших тригонометрических сумм // Известия РАН, серия математика. — 2008. — Т. 72, вып. 1 (21 апреля). — С. 161—182.
• Mei-Chu Chang. A polynomial bound in Freiman's theorem // Duke Mathematical Journal. — 2002. — Vol. 113, iss. 3 (21 April). — P. 399—419.
• Ben Green. Some Constructions in the Inverse Spectral Theory of Cyclic Groups // Combinatorics, Probability and Computing. — 2003. — Vol. 12, iss. 2 (21 April). — P. 127-138.
• Ben Green. A Szemerédi-type regularity lemma in abelian groups, with applications // Geometric & Functional Analysis GAFA. — 2005. — Vol. 15, iss. 2 (21 April). — P. 340-376.