Система коренів
- Ця стаття описує систему коренів у математиці, для опису кореневої системи рослин дивіться — корінь.
У математиці система коренів (коренева система) — це конфігурація векторів в евклідовому просторі, що задовольняє певним геометричним властивостям. Ця концепція є фундаментальною в теорії груп Лі. З тих пір як групи Лі (і деякі інші аналоги, такі як алгебричні групи) протягом двадцятого століття з'явилися в багатьох розділах математики. Більш того, класифікація систем коренів за схемами Динкіна зустрічається в розділах математики, не пов'язаних явно з групами Лі (наприклад, в теорії сингулярностей).
Означення[ред. | ред. код]
Нехай — скінченновимірний евклідів простір із звичайним скалярним добутком, позначеним як . Система корнів у — це скінченна множина ненульових векторів (званих корнями), що задовільняють наступним властивостям.

- є лінійною оболонкою системи коренів.
- Якщо два кореня , є колінеарними векторами, то або вони збігаються, або .
- Для кожного кореня множина замкнута відносно віддзеркалення в гіперплощині, що перпендикулярна . Тобто для будь-яких двох коренів і , множина містить віддзеркалення
- (Умова цілісності) Якщо і є коренями у , тоді проєкція на пряму, що проходить через , є напівцілим добутком . Тобто
Беручи до уваги властивість 3, умова цілісності еквівалентна твердженню, що різниця між та його відображенням дорівнює корню , помноженому на ціле число. Слід зазначити, що оператор
- ,
визначений властивістю 4, не є скалярним добутком. Він не симетричний і лінійний лише за першим аргументом.
Класифікація систем коренів за схемою Динкіна[ред. | ред. код]
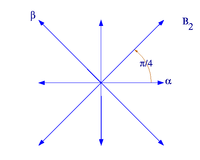
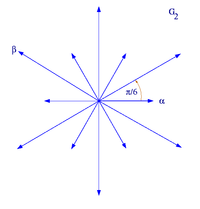
Приклади системи коренів рангу 1 і рангу 2[ред. | ред. код]
Існує тільки одна система коренів рангу 1, вона складається з двох ненульових векторів . Ця система називається .
У ранзі 2 існують чотири можливі варіанти , де .

|

|
| Система коренів | Система коренів |
|
|
| Система коренів | Система коренів |
Посилання[ред. | ред. код]
- Дынкин Е. Б. Структура полупростых алгебр Ли // Успехи математических наук. — 1947. — Т. 2, вип. 4(20). — С. 59–127.
- Дынкин Е. Б. Классификация простых групп Ли // Математический сборник. — 1946. — Т. 18(60), вип. 3. — С. 347–352.
- Хамфрис Дж. Введение в теорию алгебр Ли и их представлений / Перев. с англ. Б. Р. Френкина. — М.: МЦНМО, 2008. — 216 с.
- Винберг Э. Б., Онищик А. Л. Семинар по группам Ли и алгебраическим группам — М.: УРСС, 1995. — 344 с.
- Хамфри Дж. Линейные алгебраические группы / Пер. с англ./Под ред. В. П. Платонова. — М.: Наука, 1980. — 400 с.
- Бурбаки Н. Группы и алгебры Ли (часть 2) / Пер. с франц./Под ред. А. И. Кострикина. — М.: Мир, 1972. — 332 с.























