Коефіцієнт Жаккара
Мі́ра Жакка́ра (коефіціє́нт флористи́чної спі́льності, фр. coefficient de communaute, нім. Gemlinschaftskoefficient) — міра подібності, запропонована Полем Жаккаром в 1901 році.[1] Запропонований метод здобув поширення і нині використовується для оцінки подібності скінченних множин, в інформатиці, для пошуку подібних документів, плагіату тощо.
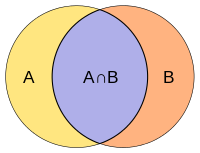
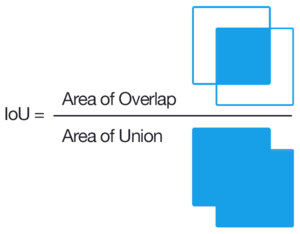
Коефіцієнт Jaccard вимірює подібність між множинами і визначається як міра спільної частини, поділена на міру об'єднання множин:
(Коли A та B обидві порожні, тоді J(A,B) = 1.)
Відстань Жаккара, яка вимірює відмінність множин, є доповненням коефіцієнта Жаккара до 1 і отримується відніманням коефіцієнта Жаккара від 1, або, еквівалентно, діленням різниці мір об'єднання і перетину двох множин на міру об'єднання:
Інакше можна пояснити відстань Жаккара, як відношення міри симетричної різниці до об'єднання.
Відстань Жаккара є метрикою на множині всіх скінченних множин[2][3][4].
В ботаніці[ред. | ред. код]
Коефіцієнт подібності Жаккара обчислюють за формулою:
- ,
де
- а — кількість видів на першому пробному майданчику,
- b — кількість видів на другому пробному майданчику,
- с — кількість видів, спільних для 1-ого та 2-ого майданчиків.
Це перший відомий коефіцієнт подібності. Прізвище автора коефіцієнта в літературі перекладалася як: Жаккард, Джаккард. Коефіцієнт Жаккара в різних модифікаціях і записах активно використовується в екології, геоботаніці, молекулярній біології, біоінформатиці, геноміці, протеїноміці, інформатиці та інших галузях. Міра Жаккара еквівалентна (пов'язані однією монотонно зростаючою залежністю) мірі Серенсена і міру Сокала-Сніта для скінченних множин (множинна інтерпретація):
Міру різниці, яка є доповненням до 1 коефіцієнта подібності Жаккара, називають мірою флористичного контрасту[5][6].
Для випадку дескриптивних множин (дескриптивна інтерпретація) в екології - це вибірки за рясністю, аналогом вказаної міри є міра Ружички[7]:
В конкретних випадках, коли використовуються компоненти булевих векторів, тобто компоненти, які набувають тільки два значення 0 та 1, міра відома під назвою коефіцієнта Танімото або розширеного коефіцієнта Жаккара[8].
Якщо порівнюються об'єкти за зустрічальністю видів (ймовірнісна інтерпретація), тобто враховуються ймовірності зустрічей, то аналогом міри Жаккара буде ймовірнісна міра Іверсена[9]:
- .
Для інформаційної аналітичної інтерпретації використовується міра взаємозалежності Райського[10][11][12]:
Мірою різниці, коеквівалентною мірі подібності Жаккара, є відстань:
В інформатиці[ред. | ред. код]
В інформатиці коефіцієнт Жаккара двох множин A та В дорівнює відношенню кількості елементів перетину множин до кількості елементів їхнього об'єднання:[13]
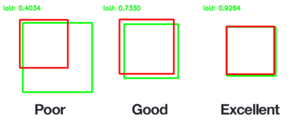
Коефіцієнт Жаккара та алгоритм шинглів використовують для пошуку схожих текстів у великому корпусі документів, а також для виявлення плагіату. Для ефективного обчислення оцінки значення коефіцієнта Жаккара використовують алгоритм MinHash.
Примітки[ред. | ред. код]
- ↑ Jaccard P. Distribution de la flore alpine dans le Bassin des Dranses et dans quelques regions voisines // Bull. Soc. Vaudoise sci. Natur. — 1901. — V. 37, Bd. 140. — S. 241—272.
- ↑ Kosub, Sven; «A note on the triangle inequality for the Jaccard distance» arXiv:1612.02696 [Архівовано 25 Квітня 2019 у Wayback Machine.]
- ↑ Lipkus, Alan H. (1999), A proof of the triangle inequality for the Tanimoto distance, Journal of Mathematical Chemistry, 26 (1-3): 263—265
- ↑ Levandowsky, Michael; Winter, David (1971), Distance between sets, Nature, 234 (5): 34—35, doi:10.1038/234034a0
- ↑ Миркин Б. М., Розенберг Г. С. Толковый словарь современной фитоценологии. — М.: Наука, 1983. — 134 с.
- ↑ Миркин Б. М., Розенберг Г. С., Наумова Л. Г. Словарь понятий и терминов современной фитоценологии. — М.: Наука, 1989. — 223 с.
- ↑ Ružička M.K. Anwendung mathematiseh-statistiseher Methoden in der Geobotanik (sintetischa Bearbeitung von Aufnahmen) // Biologia. — 1958. — Roč. 13, č. 9. — S. 647—661.
- ↑ Tanimoto T.T. IBM Internal Report — 17th Nov. — 1957.
- ↑ Iversen J. Über die Korrelationen zwischen den Pflanzenarten in einem grönlandischen Talgebiet // Vegetation. — 1954. — V. 5-6. — P. 238—246.
- ↑ Rajski C. (1961). A metric space of discrete probability distributions. Information and Control. 4 (№ 4): 371—377. doi:10.1016/S0019-9958(61)80055-7.
- ↑ Rajski C. Entropy and metric spaces // C. Cherry (ed.). Information Theory. — London: Butterworths, 1961. — P. 41-45.
- ↑ Елисеева И. И., Рукавишников В. О. Группировка, корреляция, распознавание образов: (статистические методы классификации и измерения связей). — М.: Статистика, 1977. — 143 с.
- ↑ Jure Leskovec, Anand Rajaraman, Jeffrey D. Ullman (2014). 3.1.1 Jaccard Similarity of Sets. Mining of Massive Datasets (PDF). Архів оригіналу (PDF) за 18 Вересня 2015. Процитовано 23 Вересня 2015.
Див. також[ред. | ред. код]
- Коефіцієнт подібності
- Коефіцієнт Танімото
- В ботаніці:
- Індекс Соренсена
- Коефіцієнт Кульчинського (пол. Kulczyński)
- Коефіцієнт Сімпсона
- Коефіцієнт Браун-Бланке (розроблений Жозіас Браун-Бланке)
- Коефіцієнт Охаї
- В ботаніці та кібернетиці:
Посилання[ред. | ред. код]
- Індекс Жаккара // Словник-довідник з екології : навч.-метод. посіб. / уклад. О. Г. Лановенко, О. О. Остапішина. — Херсон : ПП Вишемирський В. С., 2013. — С. 101.
- Jaccard's index and species diversity
- Introduction to Data Mining lecture notes from Tan, Steinbach, Kumar [Архівовано 4 Лютого 2012 у Wayback Machine.]
- http://sourceforge.net/projects/simmetrics/ [Архівовано 10 Січня 2013 у Wayback Machine.] SimMetrics a sourceforge implementation of Jaccard index and many other similarity metrics
- Web based tool for comparing texts using Jaccard coefficient