Шарнір (теорія графів)

Приклад графу з позначеними блоками. Кожен колір відповідає блоку. Різнокольорові вершини це шарніри, отже, вони належать кільком блокам.

Шарніром (англ. articulation point) в теорії графів називається вершина графу, при видаленні якої кількість компонент зв'язності графу зростає.

Визначення 

Вершина $v$ графу $G$ називається шарніром, якщо підграф (граф, що містить якесь підмножина вершин даного графу) $G_{1}$, отриманий з графу $G$ видаленням вершини $v$ і всіх інцидентних їй ребер, складається з більшої кількості компонент зв'язності, ніж вихідний граф $G$.

Граф, що містить два шарніра (вершини 2 і 5) і три блоки (12, 2345, 56).

Ребровим аналогом шарніра є міст. Мостом називається таке ребро графу, в результаті видалення якого кількість компонент зв'язності в графі зростає.

Алгоритм пошуку шарнірів

Ефективне вирішення завдання пошуку всіх шарнірів графу засноване на алгоритмі пошуку у глибину.

Нехай задано граф $G$. Через $Adj(v)$ позначимо множину всіх вершин графу, суміжних з $v$. Припустимо, що ми переглянули граф в глибину, почавши з деякою довільній вершини. Занумеруємо всі вершини графу в тому порядку, в якому ми в них увійшли, і кожній вершині $v$ підпорядкуємо відповідний номер $n(v)$. Якщо в вершину $u$ ми вперше потрапили з вершини $v$, то вершину $u$ будемо називати нащадком $v$, а $v$ — предком $u$. Безліч всіх нащадків вершини $v$ позначимо через $Ch(v)$. Через $Low(v)$ позначимо мінімальний номер серед всіх вершин, суміжних з $v$ і з тими вершинами, в які ми прийшли по шляху, що проходить через $v$.

Зрозуміло, що величину $Low(v)$ можна обчислити рекурсивно, безпосередньо в процесі обходу в глибину: якщо зараз розглядається вершина $v$, і з неї не можна перейти в ще не відвіданих вершину (тобто потрібно повернутися до предку $v$, або припинити обхід, якщо $v$ — стартова вершина), то для всіх її нащадків $Low$ вже пораховано, а значить, і для неї можна можна провести відповідні обчислення за формулою

$Low(v)=\min \left\{\min _{x\in Ch(v)}Low(x),\min _{y\in Adj(v)/Ch(v)}n(y)\right\}.$

Знаючи величину $Low(v)$ для всіх вершин графу, можна визначити всі його шарніри згідно з такими правилами:

1. Стартова вершина (тобто та, з якою ми почали обхід) є шарніром тоді і тільки тоді, коли у неї більше одного нащадка.
2. Вершина $v$, відмінна від стартової, є шарніром тоді і тільки тоді, коли у неї є нащадок u такий, що $Low(u)=n(v)$.

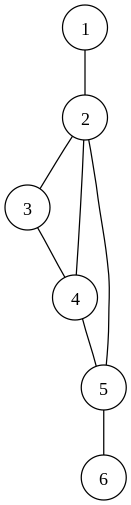
Як приклад розглянемо застосування описаного алгоритму до графу, зображеному на малюнку справа. Числа, якими позначені вершини, відповідають одному з можливих варіантів обходу в глибину. При такому порядку у кожної з вершин рівно один нащадок, за винятком вершини 6, у якій нащадків немає. Стартова вершина 1 має єдиного нащадка, отже, шарніром вона не є. Для інших вершин обчислимо значення, що цікавить нас функції:

$Low(6)=5,Low(5)=2,Low(4)=2,Low(3)=2,Low(2)=1$.

У вершини 2 є нащадок 3, а у 5 нащадок 6 — в обох випадках виконано шукане співвідношення $Low(u)=n(v)$. Отже, 2 і 5 є шарнірами. Інших шарнірів в цьому графі немає.

Псевдокод

GetArticulationPoints(i, d)
    visited[i] = true
    depth[i] = d
    low[i] = d
    childCount = 0
    isArticulation = false
    for each ni in adj[i]
        if not visited[ni]
            parent[ni] = i
            GetArticulationPoints(ni, d + 1)
            childCount = childCount + 1
            if low[ni] >= depth[i]
                isArticulation = true
            low[i] = Min(low[i], low[ni])
        else if ni <> parent[i]
            low[i] = Min(low[i], depth[ni])
    if (parent[i] <> null and isArticulation) or (parent[i] == null and childCount > 1)
        Output i as articulation point

Див. також

• Міст (теорія графів)

Посилання

• Код на С++, Python та Java для пошуку шарнірів [Архівовано 20 листопада 2016 у Wayback Machine.]