Граф одиничних відстаней

Граф Петерсена є графом одиничних відстаней: його можна зобразити на площі так, що кожне ребро буде одиничної довжини.

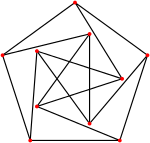
Графом одиничних відстаней у теорії графів називається граф, утворений точками на евклідовій площині, у якому ребрами з'єднані кожні дві вершини, відстань між якими дорівнює точно одиниці. Ребра графів одиничних відстаней іноді перетинаються, тож графи одиничних відстаней не завжди планарні. Граф одиничних відстаней без перетинів називається сірниковим графом.

Проблема Нельсона — Ердеша — Гадвігера стосується хроматичного числа графів одиничних відстаней. Відомо, що існують графи одиничних відстаней, що вимагають 4 кольори для правильного розфарбування і що всі такі графи можна розфарбувати не більш ніж у 7 кольорів. Інше важливе відкрите питання стосовно графів одиничних відстаней звучить так: «скільки ребер може мати такий граф відносно числа вершин?».

Приклади

Граф гіперкуба Q₄ граф одиничних відстаней.

Граф Петерсена

Інше подання графу Петерсена

Графами одиничних відстаней є такі графи:

• Будь-який цикл
• Будь-яка решітка
• Граф гіперкуба
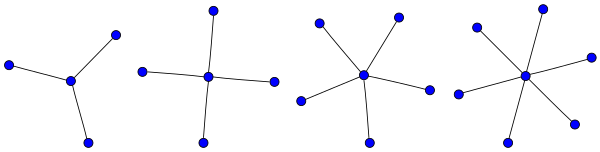
• Будь-яка зірка
• Граф Петерсена
• Граф Хівуда (Gerbracht, 2009)
• Колесо W₇
• Веретено Мозера, найменший граф одиничних відстаней з хроматичним числом 4.

Графи зірки S₃, S₄, S₅ и S₆.

Підграфи графів одиничних відстаней

Малюнок з одиничними відстанями графу Мебіуса — Кантора, в якому деякі несуміжні ребра теж перебувають на відстані одиниці.

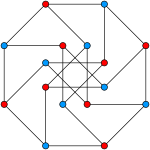
Деякі автори визначають граф одиничних відстаней як граф, який можна вкласти в площину так, що будь-які дві суміжні вершини повинні перебувати на відстані одиниці, не беручи до уваги той факт, що деякі несуміжні вершини також можуть перебувати на відстані одиниці. Наприклад граф Мебіуса — Кантора має графічне подання такого виду.

Згідно з цим визначенням узагальнені графи Петерсена є графами одиничних відстаней (Žitnik, Horvat, Pisanski, 2010). Щоб розрізняти ці два визначення введемо поняття строгого графу одиничних відстаней. У строгому графі одиничних відстаней відстань між будь-якими несуміжними вершинами повинна бути відмінною від одиниці(Gervacio, Lim, Maehara, 2008).

Граф, що утворений видаленням однієї шпиці з колеса W₇, є підграфом одиничних відстаней, але не строгим графом одиничних відстаней(Soifer, 2008, с. 94).

Підрахунок одиничних відстаней

Пал Ердеш (Erdős, 1946) запропонував завдання оцінки серед множини з n точок кількості пар, що перебувають на відстані одиниці. У термінах теорії графів питання полягає в оцінці щільності графу одиничних відстаней.

Граф гіперкуба дає нижню межу кількості одиничних відстаней, пропорційну $n\log n$. Розглядаючи точки квадратної решітки з ретельно обраною відстанню, Ердеш знайшов поліпшену нижню межу

$n^{1+c/\log \log n},$

і запропонував премію в 500 дол. за з'ясування — чи позначається максимальне число одиничних відстаней функцією того ж виду (Kuperberg, 1992). Найкраща відома межа, згідно зі Джоелем Спенсером, Ендре Семереді і Вільямом Троттером (Spencer, Szemerédi, Trotter, 1984), пропорційна

$n^{4/3};$.

Цю межу можна розглядати як число влучень точок на одиничне коло і вона тісно пов'язана з теоремою Семереді — Троттера про інцидентність точок і прямих.

Подання алгебраїчних чисел та теореми Бекмана — Куорлса

Для будь-якого алгебраїчного числа A можна знайти граф одиничних відстаней G, в якому деякі пари вершин перебувають на відстані A в усіх поданнях з одиничними відстанями G (Maehara, 1991) (Maehara, 1992). Цей результат передбачає кінцеву версію теореми Бекмана – Куорлса для будь-яких двох точок p і q, що перебувають на відстані A, існує кінцевий жорсткий граф одиничних відстаней, що містить p і q такий, що будь-яке перетворення площини, яке зберігає одиночні відстані в цьому графові, зберігає водночас і відстань між p і q (Tyszka, 2000). Повна теорема Бекмана — Куорлса стверджує, що будь-яке перетворення евклідової площини (або простору більшої розмірності), що зберігає одиничні відстані повинне бути ізометричним. Таким чином, для нескінченних графів одиничних відстаней, вершинами яких є всі точки на площині, будь-який автоморфізм графів повинен бути ізометричним (Beckman, Quarles, 1953).

Узагальнення на більші розмірності

Визначення графу одиничних відстаней можна природним чином узагальнити на будь-яку розмірність евклідового простору. Будь-який граф можна вкласти у вигляді набору точок у простір досить високої розмірності. Маехара і Редль (Maehara, Rödl, 1990) показали, що розмірність, необхідну для вкладення графу, можна обмежити подвоєнням його максимального ступеню.

Необхідна для вкладення графу розмірність, при якій всі ребра матимуть одиничну довжину, і розмірність вкладення, при якій ребра будуть з'єднувати саме ті точки, між якими відстань одиниця, можуть істотно відрізнятися. Корону з 2n вершинами можна вкласти в чотиривимірний простір так, що всі її ребра будуть мати одиничну відстань, але потрібно розмірність щонайменше n − 2, щоб вкласти її так, щоб не було пар вершин, які перебувають на відстані одиниці і водночас не з'єднані ребром (Erdős, Simonovits, 1980).

Обчислювальна складність

NP-складною задачею, точніше повною задачею для теорії існування дійсних чисел називається задача перевірки, чи є певний граф просто графом одиничних відстаней, або ж він є строгим графом одиничних відстаней(Schaefer, 2013).

Див. також

• Граф одиничних кругів

Література

• F. S. Beckman, D. A., Jr. Quarles. On isometries of Euclidean spaces. — 1953. — Т. 4. — С. 810-815. — DOI:10.2307/2032415..
• Paul Erdős. [[[The American Mathematical Monthly|American Mathematical Monthly]] On sets of distances of n points]. — American Mathematical Monthly. — 1946. — Т. 53. — С. 248—250. — DOI:10.2307/2305092..

• On the chromatic number of geometric graphs. — Ars Combinatoria. — 1980. — Т. 9. — С. 229—246. Як цитовано в Soifer, 2008, с. 97.
• Eberhard H.-A. Gerbracht. Eleven unit distance embeddings of the Heawood graph. — 2009. — arXiv:0912.5395..
• Severino V. Gervacio, Yvette F. Lim, Hiroshi Maehara. Planar unit-distance graphs having planar unit-distance complement. — Discrete Mathematics. — 2008. — Т. 308. — С. 1973—1984. — DOI:10.1016/j.disc.2007.04.050..
• Itai Alon, Maehara Szwarcfiter, Christos H., Papadimitriou, Jayme Luiz. Hamilton paths in grid graphs. — SIAM Journal on Computing. — 1982. — Т. 11. — С. 676–686. — DOI:10.1137/0211056..
• Greg Kuperberg. The Erdos kitty: At least $9050 in prizes!. — 1992. — Т. Posting to usenet groups rec.puzzles and sci.math.
• Hiroshi Maehara. Discrete Applied Mathematics. — 1991. — Т. 31. — С. 193—200. — DOI:10.1016/0166-218X(91)90070-D.
• Hiroshi Maehara. Extending a flexible unit-bar framework to a rigid one. — Discrete Mathematics. — 1992. — Т. 1-3. — С. 167–174. — DOI:10.1016/0012-365X(92)90671-2..
• Hiroshi Maehara. On the dimension to represent a graph by a unit distance graph.. — 1990. — С. 365–367. — DOI:10.1007/BF01787703.
• Schaefer Marcus. Thirty Essays on Geometric Graph Theory. — Springer. — 2013. — С. 461–482. — DOI:10.1007/978-1-4614-0110-0_24..
• Alexander Soifer. The Mathematical Coloring Book. — Springer-Verlag. — 2008. — ISBN 978-0-387-74640-1..
• Joel Spencer,Ендре Семереді, William T. Graph Theory and Combinatorics. — Academic Press. — P. 293–308. — ISBN 0-12-111760-X..
• Tyszka Apoloniusz. Discrete versions of the Beckman-Quarles theorem // Aequationes Mathematicae. — 2000. — Т. 1-2. — С. 124–133. — DOI:10.1007/PL00000119..
• Žitnik Arjana,Horvat Boris,Tomaž Pisanski. All generalized Petersen graphs are unit-distance graphs. — 2010. — (IMFM preprints).

Посилання

• Venkatasubramanian, Suresh, Problem 39: Distances among Point Sets in R² and R³, Архівована копія, архів оригіналу за 30 серпня 2006, процитовано 24 березня 2016 {{citation}}: Вказано більш, ніж один |заголовок= та |title= (довідка)Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання).
• Weisstein, Eric W. Unit-Distance Graph(англ.) на сайті Wolfram MathWorld.