Структурна жорсткість
У дискретній геометрії та механіці структурна жорсткість є комбінаторною теорією для передбачення гнучкості ансамблів, утворених твердими тілами, з'єднаними гнучкими ланками або шарнірами .
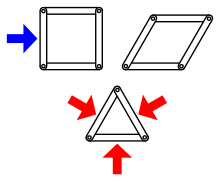
Жорсткість — це властивість конструкції, яка полягає в тому, що вона не згинається і не прогинається під дією прикладеної сили. Протилежністю жорсткості є гнучкість. У теорії структурної жорсткості конструкції утворюються наборами об'єктів, які самі по собі є твердими тілами, часто приймають прості геометричні форми, такі як прямі стрижні (відрізки), з парами об'єктів, з'єднаних гнучкими шарнірами. Конструкція є жорсткою, якщо вона не може згинатися; тобто якщо немає безперервного руху конструкції, яка зберігає форму своїх жорстких компонентів і схему їх з'єднань на шарнірах.
Є два принципово різних види жорсткості. Скінченна або макроскопічна жорсткість означає, що конструкція не буде згинатися, складатися або згинатися на позитивну величину. Нескінченно мала жорсткість означає, що конструкція не прогинається навіть на величину, яка є надто малою, щоб її можна було виявити навіть теоретично. (Технічно це означає, що певні диференціальні рівняння не мають ненульових розв'язків.) Важливість скінченної жорсткості очевидна, але нескінченно мала жорсткість також має вирішальне значення, оскільки нескінченно мала гнучкість у теорії відповідає незначному вигину в реальному світі та, як наслідок, погіршенню конструкції.
Жорсткий граф — це вкладення графа в евклідів простір, яке є структурно жорстким.[1] Тобто граф є жорстким, якщо жорсткою є структура, утворена заміною ребер на жорсткі стрижні, а вершин на гнучкі шарніри. Граф, який не є жорстким, називається гнучким. Більш формально, вкладення графа є гнучким, якщо вершини можна безперервно переміщувати, зберігаючи відстані між сусідніми вершинами, в результаті чого відстані між деякими несуміжними вершинами змінюються.[2] Остання умова виключає евклідові конгруенції, такі як простий переклад і поворот.
Також можна розглядати проблеми жорсткості для графів, у яких деякі ребра представляють елементи стиснення (здатні розтягуватися до більшої довжини, але не стискатися до меншої довжини), тоді як інші ребра представляють елементи розтягування (здатні стискатися, але не розтягуватися). Жорсткий граф із ребрами цих типів утворює математичну модель структури тенсегріті.

Фундаментальна проблема полягає в тому, як передбачити жорсткість конструкції за допомогою теоретичного аналізу, не будуючи її. Основні результати в цій галузі включають наступне:
- У будь-якому вимірі жорсткість стрижнево-шарнірних зв'язків описується матроїдом. Основою двовимірного матроїда жорсткості[en] (мінімально жорстких графів на площині) є графи Ламана.
- Теорема Коші стверджує, що тривимірний опуклий багатогранник, побудований із жорсткими пластинами для його граней, з'єднаних шарнірами по краях, утворює жорстку структуру.
- Гнучкі многогранники, неопуклі багатогранники, які не є жорсткими, були побудовані Раулем Брікаром[en], Робертом Коннеллі та іншими. Гіпотеза сильфона, тепер доведена, стверджує, що кожен безперервний рух гнучкого многогранника зберігає його об'єм .
- У задачі скріплення сітки[en], де каркас, який потрібно зробити жорстким, є квадратною сіткою з доданими діагоналями у якості поперечних кріплень[en], жорсткість структури можна проаналізувати, перевівши її в проблему зв'язності основного дводольного графа.[3][4]
Однак у багатьох інших простих ситуаціях ще не завжди відомо, як математично проаналізувати жорсткість конструкції, попри існування значної математичної теорії.
Одним із засновників математичної теорії структурної жорсткості був видатний фізик Джеймс Клерк Максвелл. Наприкінці двадцятого століття стався розквіт математичної теорії жорсткості, який продовжується у двадцять першому столітті.
«[А] теорія рівноваги та прогинів каркасів, що піддаються дії сил, діє на твердість якості… у випадках, коли каркас… зміцнюється додатковими сполучними елементами… у випадках трьох розмірів, за звичайним методом рівнянь сил, кожна точка матиме три рівняння для визначення її рівноваги, щоб дати 3s рівнянь між e невідомими величинами, якщо s — кількість точок, а e — кількість з'єднань [sic]. Є, однак, шість рівнянь рівноваги системи, які обов'язково повинні виконуватися силами через рівність дії та протидії в кожній частині. Отже, якщо e = 3s − 6, ефект будь-якої вічної сили буде певним у створенні напруги або тиску в різних частинах; але якщо e > 3s − 6 ці сили будуть невизначеними. . . .»[5]
- ↑ Weisstein, Eric W. Rigid Graph(англ.) на сайті Wolfram MathWorld.
- ↑ Weisstein, Eric W. Flexible Graph(англ.) на сайті Wolfram MathWorld.
- ↑ Baglivo, Jenny A.; Graver, Jack E. (1983), 3.10 Bracing structures, Incidence and Symmetry in Design and Architecture, Cambridge Urban and Architectural Studies, Cambridge, UK: Cambridge University Press, с. 76—87, ISBN 9780521297844
- ↑ Graver, Jack E. (2001), Counting on Frameworks: Mathematics to Aid the Design of Rigid Structures, The Dolciani Mathematical Expositions, т. 25, Washington, DC: Mathematical Association of America, ISBN 0-88385-331-0, MR 1843781.
- ↑ Maxwell, James Cleark (1864), On reciprocal figures and diagrams of forces, Philosophical Magazine, 4th Series, т. 27, № 182, с. 250—261, doi:10.1080/14786446408643663
- Alfakih, Abdo Y. (2007), On dimensional rigidity of bar-and-joint frameworks, Discrete Applied Mathematics[en], 155 (10): 1244—1253, doi:10.1016/j.dam.2006.11.011, MR 2332317.
- Connelly, Robert (1980), The rigidity of certain cabled frameworks and the second-order rigidity of arbitrarily triangulated convex surfaces, Advances in Mathematics[en], 37 (3): 272—299, doi:10.1016/0001-8708(80)90037-7, MR 0591730.
- Crapo, Henry (1979), Structural rigidity, Structural Topology (1): 26—45, 73, MR 0621627.
- Maxwell, J. C. (1864), On reciprocal figures and diagrams of forces, Philosophical Magazine, 4th Series, 27 (182): 250—261, doi:10.1080/14786446408643663.
- Rybnikov, Konstantin; Zaslavsky, Thomas (2005), Criteria for balance in abelian gain graphs, with applications to piecewise-linear geometry, Discrete and Computational Geometry[en], 34 (2): 251—268, arXiv:math/0210052, doi:10.1007/s00454-005-1170-6, MR 2155721.
- Whiteley, Walter (1988), The union of matroids and the rigidity of frameworks, SIAM Journal on Discrete Mathematics, 1 (2): 237—255, doi:10.1137/0401025, MR 0941354