Квадрат (алгебра)

y=x², при цілих значениях x на відрізку від 1 до 25

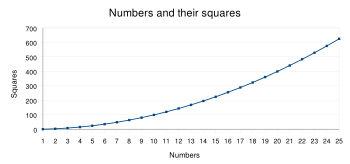
Квадра́том числа називається результат множення числа на себе (піднесення числа до степеня 2).

Далі наведений початок числової послідовності для квадратів цілих невід'ємних чисел (Послідовність A000290 з Енциклопедії цілочисельних послідовностей):

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849…

Квадрат натурального числа $n$ можна також записати у вигляді суми перших $n$ непарних чисел:

1: $1 = 1$

2: $4 = 1 + 3$

…

7: $49 = 1 + 3 + 5 + 7 + 9 + 11 + 13$

…

Ще один спосіб запису квадрату натурального числа:

$n^2 = 1 + 1 + 2 + 2 + ... + (n - 1) + (n - 1) + n$

Приклад:

1: $1 = 1$

2: $4 = 1 + 1 + 2$

…

4: $16 = 1 + 1 + 2 + 2 + 3 + 3 + 4$

…

Сума квадратів перших $n$ натуральных чисел обчислюється за формулою:

$\sum_{i=1}^n i^2 = 1^2 + 2^2 + 3^2 + ... + n^2 = \frac {n(n + 1)(2n + 1)} {6}$

Квадрат комплексного числа

Квадрат комплексного числа в алгебраїчній формі можна обчислити за формулою:

$\left(a+bi\right)^2 = \left(a^2 - b^2\right) + 2abi.$

Аналогічна формула для комплексного числа у тригонометричній формі:

$r\left(\cos\phi+i\sin\phi\right)^2 = r^2\left(\cos{2\phi}+i\sin{2\phi}\right).$

Геометричний зміст

Квадрат числа дорівнює площі квадрату зі стороною, яка дорівнює цьому числу.

Див. також

• Отримання квадратного кореня — зворотна операція по відношенню до піднесення до квадрату.
• Куб
• Квадратична функція