Площа
| Площа | ||||
| Прямокутник із розмірами сторін 5x4 має площу 20 | ||||
| Символи: | S або A | |||
|---|---|---|---|---|
| Одиниці вимірювання | ||||
| SI | м2 | |||
| СГС | см2 | |||
| Розмірність: | L2 | |||
|
| ||||
Пло́ща — фізична величина, що визначає розмір поверхні, одна з основних властивостей геометричних фігур, у математиці розглядається як міра множини точок, які займають поверхню або якусь її частину[1]. Історично, обчислення площі називалося квадратурою. Фігура, що має площу, називається квадрованою. Площу нескладних геометричних фігур визначають, підраховуючи кількість одиничних квадратів, якими фігури можна покрити. Фігури, що мають однакову площу називають рівновеликими.
Загальний метод обчислення площі геометричних фігур надало інтегральне числення. Узагальненням поняття площі стала теорія міри множини, яка є придатною для ширшого класу геометричних об'єктів.
Площа у системі SI вимірюється у м² (метрах квадратних). Площу заведено позначати великою латинською літерою S, у англомовній літературі — великою латинською літерою A (від англ. area)[2][3].
Формальне визначення[ред. | ред. код]

Площею в планіметрії може назватися будь-яка величина, яка задовольняє умовам[4][5]:
- вона додатно-визначена (тобто не менша від нуля);
- вона адитивна (площа об'єднання двох фігур, що не перетинаються, дорівнює сумі площ цих двох фігур);
- у конгруентних фігур площа однакова;
- для квадрата зі стороною 1 вона приймається рівною 1.
З даного визначення площі випливає її монотонність, тобто площа частини фігури є меншою від площі всієї фігури.
Спочатку визначення площі було сформульоване для многокутників, згодом воно було розширене на квадровані фігури. Квадрованою називається така фігура, яку можна вписати у многокутник і у яку можна вписати многокутник, причому площі обох многокутників різняться на довільно малу величину. Такі фігури називають також вимірними за Жорданом[5]. Для фігур на площині, які не складаються з цілої кількості одиничних квадратів, а також для тривимірних поверхонь, площа визначається за допомогою граничного переходу.
Історична довідка[ред. | ред. код]
Площа плоских фігур[ред. | ред. код]
Протягом багатьох років площа вважалася первинним поняттям, яке не вимагає визначення. Основним завданням математиків було обчислення площі, при цьому їм були відомі основні її властивості[4]. У Стародавньому Єгипті використовувались точні правила обчислення площі прямокутників, прямокутних трикутників і трапецій, площа довільного чотирикутника визначалась приблизно як добуток півсум пар протилежних сторін. Застосування такої наближеної формули пов'язане з тим, що ділянки, площу яких треба було визначити, були в основному близькими до прямокутних і похибка у такому випадку залишалась невеликою. Історик математики А. П. Юшкевич припускає, що єгиптяни могли і не знати, що користуються наближеною формулою. У задачі 50 папірусу Рінда використовується формула обчислення площі круга, яка вважалась рівною площі квадрата зі стороною, рівною 8/9 діаметра круга[6]. Такими ж формулами користувались і у Вавилоні, однак для площі круга наближення було менш точним. Крім того, вавилоняни могли наближено обчислити площі правильних п'яти-, шести- і семикутника зі стороною рівною одиниці. У шістдесятковій системі їм відповідали 1,40, 2,37,20 і 3,41, відповідно[7].
Основним прийомом обчислення площі при цьому була побудова квадрата, площа якого дорівнює площі заданої багатокутної фігурі, зокрема у книзі I «Начал» Евкліда, що присвячена планіметрії прямолінійних фігур, доводиться, що трикутник є рівновеликим половині прямокутника, що має з ним одинакові основи і висоту[8]. Метод розкладання, що ґрунтувався на тому, що дві рівноскладені фігури є рівновеликими, дозволяв також обчислити площі паралелограмів й довільних многокутників[9].
Наступним кроком було обчислення площ круга, кругового сектора, лунок та інших фігур. Основу обчислень при цьому становив метод вичерпування многокутниками[5][9], з якого бере початок теорія границь. Метод полягає у побудові послідовності площ, які при поступовому нарощуванні «вичерпують» площу, що розглядається. Метод вичерпування, який отримав свою назву лише у XVII столітті, ґрунтується на аксіомі неперервності Евдокса — Архімеда, авторство якої приписується Евдоксу Кнідському, котрий за її допомогою показав, що площі кругів відносяться одна до одної як квадрати їх діаметрів. Метод описаний у «Началах» Евкліда: аксіома Евдокса сформульована у книзі V, а сам метод вичерпування і відношення, що ґрунтуються на ньому — у книзі XII[8]. Більшої досконалості у застосуванні методу досягнув Архімед, котрий за його допомогою вирахував площу сегмента параболи та площу поверхні сфери[10][11]. Праця Архімеда «Про спіралі» містить багато тверджень, що стосуються площ різних витків спіралі та їх співвідношень[12]. Архімеду належить ідея використання площ або об'ємів як вписаних, так і описаних фігур для визначення величини заданої площі чи об'єму[13].
У Стародавній Індії на початках користувались тією ж формулою для обчислення площ чотирикутників, що й єгиптяни та греки. Брамагупта використовував формулу для обчислення площі чотирикутників, виражену через їх півпериметр, що давала вірне значення для вписаного у коло чотирикутника. Формули обчислення площі зазвичай не доводились, але демонструвались з наочними рисунками[14]. Формула Брамагупти є аналогом формули Герона для площі трикутника, яку той навів у своїй «Метриці»[15].
Розвиток та узагальнення методу вичерпування відбулися лише у XVII столітті. У 1604 році у праці «Три книги про центр тяжіння тіл» Лука Валеріо (італ. Luca Valerio 1552—1618) широко використовує теорему, за якою різниця між площами вписаної і описаної фігур, складених з паралелограмів можна зробити меншою від будь-якої заданої площі[16]. Справжній прорив було зроблено Й. Кеплером, якому для астрономічних розрахунків потрібно було вміти обчислювати площу еліпса. Кеплер розглядав площу як «суму ліній» і, розліновуючи еліпс з кроком у один градус, показав[17], що . Б. Кавальєрі, обґрунтовуючи схожий метод, названий «методом неподільних», порівнював площі плоских фігур, використовуючи перетин фігур паралельними прямими[18]. Застосування первісної для знаходження площі плоскої фігури є найуніверсальнішим методом. За допомогою первісної доводиться принцип Кавальєрі, за яким дві плоскі фігури мають однакову площу, якщо при перетині кожної з них прямою, паралельною до фіксованої, отримуються відрізки однакової довжини. Принцип був відомий задовго до формування інтегрального числення[5][9].
Площа поверхонь[ред. | ред. код]
Обчисленням площ кривих поверхонь займався Архімед, визначивши, зокрема, площу поверхні кулі [13]. У загальному випадку для визначення площі поверхні неможливо скористатися а ні розгорткою (не підходить для сфери), а ні наближенням багатогранними поверхнями (аналогом методу вичерпування). Останнє продемонстрував Г. Шварц, побудувавши для бічної поверхні циліндра послідовності, які приводять до різних результатів (так званий «чобіт Шварца»)[5][19].
Загальний прийом обчислення площі поверхні на рубежі XIX—XX століть запропонував Г. Мінковський, який для кожної поверхні будував «огортальний шар» малої сталої товщини, тоді площа поверхні буде приблизно рівною об'єму цього шару, поділеному на його товщину. Граничне значення цього відношення при товщині шару, що прямує до нуля дає точне значення площі. Однак, для площі за Мінковським не завжди виконується властивість адитивності. Узагальнення даного визначення приводить до поняття лінії за Мінковським[20].
Площа в аналітичній геометрії[ред. | ред. код]
Аналітична геометрія дозволяє розв'язувати геометричні задачі алгебраїчними методами, оперуючи такими поняттями як система координат, вектор тощо. Площина в тривимірному просторі має дві поверхні. Площі цих двох поверхонь позначаються із протилежними знаками. Оскільки орієнтація поверхні задається вектором нормалі до неї, то площу теж визначають як вектор, колінеарний нормалі до поверхні.
Наприклад, для паралелограма, побудованого на векторах та площа визначається як векторний добуток:
- .
При зміні порядку множників у цій формулі, міняє знак, що відповідає нормалям до двох різних боків поверхні. Як добуток двох векторів є псевдовектором — при зміні напрямку кожного із векторів та на протилежний, напрямку не міняє.
Площа в математичному аналізі[ред. | ред. код]
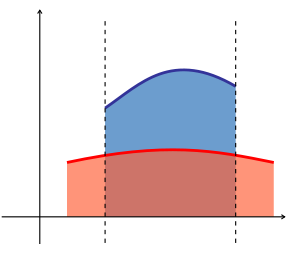
Математичний аналіз надає широкі можливості для обчислення площ криволінійних фігур. Поняття інтеграла, яке має широке застосування і в інших галузях, має просту інтерпретацію, як площа криволінійної фігури обмеженої підінтегральною функцією, віссю абсцис і двома прямими, паралельними осі ординат:
- .
Оскільки функція може мати як додатні, так і від'ємні значення на інтервалі [a, b], то інтеграл теж може бути додатнім або від'ємним. Для того, щоб отримати площу фігури в її геометричному сенсі потрібно інтегрувати абсолютну величину функції:
- .
Виходячи з цього означення, площу між двома графіками функцій можна знайти як інтегралів однієї функції, f(x), мінус інтеграл іншої функції, g(x).
- .
Площу криволінійної фігури, обмеженої функцією , вираженою в полярних координатах, знаходять за формулою
- .
Площу обмежену параметричною кривою з кінцевими точками знаходять за теоремою Гріна криволінійним інтегралом
Водночас, ця формула є z-координатою векторного добутку:
В цій формулі крапка над означає похідну.
Для поверхні у тривимірному просторі, заданої функцією над деякою областю (або є проєкцією поверхні на площину [21]):
Корисні рівняння[ред. | ред. код]
Поширені рівняння для обчислення площі планіметричних фігур[ред. | ред. код]
| Фігура | Рівняння | Змінні |
|---|---|---|
| Квадрат | — довжина сторони квадрата. | |
| Правильний трикутник | — довжина сторони трикутника. | |
| Правильний шестикутник | — довжина сторони шестикутника. | |
| Правильний восьмикутник | — довжина сторони восьмикутника | |
| Правильний багатокутник | — периметр, а — кількість сторін. | |
| Правильний багатокутник (кути в градусах) | — периметр, а — кількість сторін. | |
| Прямокутний трикутник | і — катети трикутника. | |
| Довільний трикутник | — сторона трикутника, — висота, проведена до цієї сторони. | |
| , — будь-які дві сторони, — кут між ними. | ||
| (формула Герона) | , , — сторони трикутника, — півпериметр . | |
| у випадку обходу вершин трикутника за годинниковою стрілкою отримаємо додатний результат, інакше від'ємний. | ||
| Прямокутник | та — довжини сторін прямокутника (його довжина та ширина). | |
| Паралелограм | та — довжина сторони та опущеної на неї висоти відповідно. | |
| і — сусідні сторони паралелограма, — кут між ними. | ||
| Ромб | та — довжини діагоналей ромба | |
| Трапеція | та — паралельні сторони а — відстань між ними (висота трапеції) | |
| Довільний чотирикутник | (формула Брамагупти) |
, , , — сторони чотирикутника, — його півпериметр, — півсума протилежних кутів кутів чотирикутника |
| Довільний многокутник (опуклий і неопуклий) | (метод трапецій) |
— координати вершин многокутника за порядком їх обходу, замикаючи останню з першою: ; при наявності отворів напрям їх обходу — протилежний до напряму обходу зовнішньої границі многокутника |
| Еліпс | та — довжини малої та великої півосей відповідно |
Формули для обчислення площі поверхні тіл у просторі[ред. | ред. код]
| Тіло | Рівняння | Змінні |
|---|---|---|
| Повна площа поверхні циліндра | та — радіус та висота відповідно. | |
| Площа бічної поверхні циліндра | та — радіус та висота відповідно. | |
| Повна площа конуса | та — радіус та висота бічної поверхні відповідно. | |
| Площа бічної поверхні конуса | та — радіус та твірна бічної поверхні відповідно. | |
| Площа поверхні сфери (кулі) | або | та радіус та діаметр, відповідно. |
Наведені вище формули призначені для обчислення площі багатьох фігур.
Формули для обчислення площі круга, його частин, описаних і вписаних у коло фігур[ред. | ред. код]
| Фігура | Рівняння | Змінні |
|---|---|---|
| Круг | або | — радіус, а — діаметр круга. |
| Сектор круга | — радіус круга, — центральний кут сектора (в радіанах). | |
| Сегмент круга | — радіус круга, — центральний кут сегмента (в радіанах). | |
| Трикутник, вписаний у коло | , , — сторони трикутника, — радіус описаного кола. | |
| Довільний багатокутник, описаний навколо кола | — радіус кола, вписаного в багатокутник, а — периметр багатокутника. |
Вимірювання площ[ред. | ред. код]

Прилад, що слугує для простого механічного визначення площ (інтегрування) плоских замкнутих контурів носить назву планіметр.
Найбільше використовувалась одна з можливих реалізацій даного приладу — планіметр Амслера-Кораді, фактично є частковим випадком аналогового обчислювального пристрою. Основними частинами найпоширенішого планіметра є обвідний важіль з штифтом, який обводить контур фігури і лічильний механізм, що, фіксуючи переміщення штифта, вказує шукану величину площі[22].
Одиниці вимірювання площ[ред. | ред. код]
Метричні одиниці[ред. | ред. код]


- Квадратний кілометр, 1 км² = 1 000 000 м²;
- Гектар, 1 га = 10 000 м²;
- Ар (сотка), 1а = 100 м²;
- Квадратний метр, похідна одиниця системи SI[23];
- Квадратний сантиметр, 1 см² = 0,0001 м²;
- Квадратний міліметр, 1 мм² = 0,000 001 м².
Британські/американські одиниці[ред. | ред. код]
- Квадратний дюйм, 1 in² = 0,000645 м²;
- Квадратний фут, 1 ft² = 144 in² = 0,09 м²;
- Квадратний ярд, 1 yr² = 9 ft² = 0,84 м²;
- 1 квадратна миля = 2589987,83 м² = 2,59 км².
Стародавні одиниці[ред. | ред. код]
- Морг (Середньовічна Європа), найчастіше 1 морг = 0,57 га = 5700 м² (прусський морг — 0,2553 га)
- Дуньом (Османська імперія), 1 дунам = 919,3 м²
- Арура (Стародавній Єгипет), 1 арура = 2735,29 м²
- Плефр (Візантія), 1 плефр = 1261,9 м²
- Унція (Римська імперія), 1 унція = 209,91 м²
- Югер (Римська імперія)), 1 югер = 12 унцій = 2519 м²
- Центурія (Римська імперія), 1 центурія = 200 югерів = 503800 м².
Площі деяких об'єктів[ред. | ред. код]
| Об'єкт | Площа у квадратних метрах |
|---|---|
| Ядерна пора | 2×10-14[24] |
| Бактерія E. coli | 6×10-12[26] |
| Піксель у LCD дісплеї 3D-окулярів | 7×10-11[27] |
| Переріз людської волосини | 5×10-9 |
| Центральна ямка ока | 9×10-8 |
| Дірка від діркопробивача | 4×10-5 |
| Поштова марка | 5×10-4 |
| Кредитна картка | 4,6×10-3 |
| Лист А4 | 0,0625 |
| Баскетбольний м'яч | 0,18 |
| Середня площа людини | 1,73[28] |
| Легені людини | 70[29] |
| Футбольне поле | 7140 |
| Майдан Свободи (Харків) | 119 000 |
| Ватикан | 440 000 |
| Монако | 2×106 |
| Шпола (17000 жителів) | 6,1×107 |
| Київ | 8,4×108 |
| Озеро Сиваш | 4×109 |
| Чернівецька область | 8×109 |
| Шрі-Ланка | 6,5×1010 |
| Україна | 6×1011 |
| Римська імперія (максимальна площа) | 5×1012[30] |
| Місяць | 3,7×1013 |
| Земля | 5,1×1014 |
| Нептун | 7,6×1015 |
| Юпітер | 6,1×1016 |
| Сонце | 6,1×1018 |
| Альдебаран | 11,8×1021 |
| Бетельгейзе | 4,8×1024 |
| UY Щита | 1,8×1025 |
| Площа, що замітається Плутоном при переміщенні по орбіті | 1,1×1026 |
| Хмара Оорта | 5,1×1032 |
| Чумацький Шлях (приблизна площа галактичного диску) | 5,1×1032[31] |
Див. також[ред. | ред. код]
- Площа поверхні
- Метод вичерпування
- Поверхневий інтеграл
- Принцип Кавальєрі
- Одна сьома площі трикутника
- Найбільший многокутник одиничного діаметра
Примітки[ред. | ред. код]
- ↑ «Площа» [Архівовано 26 березня 2017 у Wayback Machine.] // Українська радянська енциклопедія : у 12 т. / гол. ред. М. П. Бажан ; редкол.: О. К. Антонов та ін. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985.
- ↑ ДСТУ 3651.1-97 Похідні одиниці фізичних величин міжнародної системи одиниць та позасистемні одиниці. Основні поняття, назви та позначення.
- ↑ Bureau international des poids et mesures (2006). The International System of Units (SI) (PDF). 8th ed. Архів оригіналу (PDF) за 5 листопада 2013. Процитовано 13 лютого 2008. Chapter 5. (англ.)
- ↑ а б Энциклопедия элементарной математики, кн. 5, 1966, с. 7—13.
- ↑ а б в г д Площадь // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия, 1982. — Т. 4.
- ↑ История математики, т. I, 1970, с. 30—32.
- ↑ История математики, т. I, 1970, с. 47—53.
- ↑ а б История математики, т. I, 1970, с. 111—114.
- ↑ а б в Болтянский В. О понятиях площади и объёма. [Архівовано 5 травня 2017 у Wayback Machine.] Квант, № 5, 1977, c.2—9
- ↑ Исчерпывания метод // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия, 1982. — Т. 2.
- ↑ История математики, т. I, 1970, с. 101—105.
- ↑ Boyer & Merzbach, 2010, с. 127—128.
- ↑ а б История математики, т. I, 1970, с. 117—124.
- ↑ История математики, т. I, 1970, с. 197—198.
- ↑ Boyer & Merzbach, 2010, с. 172, 219.
- ↑ История математики, т. II, 1970, с. 131—135.
- ↑ История математики, т. II, 1970, с. 166—171.
- ↑ История математики, т. II, 1970, с. 174—181.
- ↑ Дубровский В. Н. В поисках определения площади поверхности [Архівовано 27 червня 2017 у Wayback Machine.] // Квант. — 1978. № 5. — С.31—34.
- ↑ Дубровский В. Н. Площадь поверхности по Минковскому [Архівовано 15 лютого 2017 у Wayback Machine.] // Квант. — 1979. № 4. — С.33—35.
- ↑ Мышкис А. Д. (1973). Лекции по Высшей Математике.
- ↑ «Планіметр» [Архівовано 26 березня 2017 у Wayback Machine.]// Українська радянська енциклопедія : у 12 т. / гол. ред. М. П. Бажан ; редкол.: О. К. Антонов та ін. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985.
- ↑ Bureau International des Poids et Mesures Resolution 12 of the 11th meeting of the CGPM (1960) [Архівовано 28 липня 2012 у Wayback Machine.], retrieved 15 July 2012
- ↑ Gateway to the Nucleus [Архівовано 2013-08-22 у Wayback Machine.](англ.)
- ↑ []
- ↑ General Statistics(англ.)
- ↑ DPI Calculator [Архівовано 17 липня 2020 у Wayback Machine.](англ.)
- ↑ The Average Body Surface Area of Adult Cancer Patients in the UK: A Multicentre Retrospective Study [Архівовано 3 березня 2022 у Wayback Machine.](англ.)
- ↑ Lung Surfactants: Basic Science and Clinical Applications [Архівовано 22 липня 2020 у Wayback Machine.](англ.)
- ↑ East-West Orientation of Historical Empires and Modern States [Архівовано 17 травня 2016 у Portugese Web Archive](англ.)
- ↑ The Milky Way [Архівовано 10 серпня 2015 у Wayback Machine.](англ.)
Джерела[ред. | ред. код]
- Борисенко О. А. Диференціальна геометрія і топологія: Навч. посібник для студ. — Харків : Основа, 1995. — 304 с. — ISBN 5-7768-0388-8.
- Геометрия // Энциклопедия элементарной математики / Под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М. : Наука, 1966. — Т. 5. — 624 с.(рос.)
- Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1900+ с.(укр.)
- С древнейших времён до начала Нового времени // История математики: в 3 т / Под редакцией А. П. Юшкевича. — М. : Наука, 1970. — Т. 1. — 352 с.(рос.)
- Математика XVII столетия // История математики: в 3 т / Под редакцией А. П. Юшкевича. — М. : Наука, 1970. — Т. 2. — 300 с.(рос.)
- Boyer C. B., Merzbach U. C. — John Wiley & Sons, 2010. — 640 с. Архівовано з джерела 9 липня 2019(англ.)
Посилання[ред. | ред. код]
- Обчислення площ плоских фігур // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 425. — 594 с.
| Вікісховище має мультимедійні дані за темою: Площа |
- Формули площі геометричних фігур [Архівовано 28 квітня 2017 у Wayback Machine.] на сайті «OnlineMSchool»
- Гейдман Б. П. Площади многоугольников [Архівовано 10 червня 2017 у Wayback Machine.]. — М.: МЦНМО, 2001 — 24 с. — (Библиотека «Математическое просвещение», выпуск 9). — ISBN 5-900916-72-3.
|




![{\displaystyle \mathbf {S} =[\mathbf {a} \times \mathbf {b} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4e7651b0380d075a7654fb37809b83b84ea78c6)































































