Дерево (структура даних)

Де́рево (англ. tree) — в інформатиці та програмуванні одна з найпоширеніших структур даних[1]. Формально дерево визначається як скінченна множина Т з однією або більше вершин (вузлів, nodes), яка задовольняє наступні вимоги:
- існує один відокремлений вузол — корінь (root) дерева;
- інші вузли (за винятком кореня) розподілені серед m ≥ 0 непересічних множин T1…Tm і кожна з цих множин, в свою чергу, є деревом. Дерева T1…Tm мають назву піддерев (subtrees) даного кореня.
Визначення[ред. | ред. код]
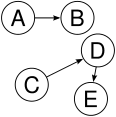
Дерево (можливо, нелінійне) — структура даних, яка складається з вузлів (вершин) і ребер, без будь-яких циклів. Дерево без вузлів називається нульовим або порожнім деревом. Дерево, яке не є порожнім, складається з кореневого вузла і багатьох рівнів додаткових вузлів, які утворюють ієрархію.
 |
 |
 |
 |
 |
Використовувана термінологія[ред. | ред. код]
- Корінь — верхній вузол в дереві.
- Дитина — вузол, безпосередньо приєднаний до іншого на шляху від кореня.
- Батько — зворотне поняття до дитини.
- Брати, сестри — вузли з того ж батька.
- Нащадок — вузол, досяжний послідовними переходами від батька до дитини.
- Предок — вузол, досяжний послідовними переходами від дитини до батька.
- Лист (також Зовнішній вузол) — вузол, який не має дітей.
- Внутрішній вузол — вузол, який має щонайменше одну дитину.
- Степінь вузла — кількість піддерев даного вузла.
- Ребро — з'єднання від одного вузла до іншого.
- Шлях — послідовність вершин і ребер, що з'єднують вузол з нащадком.
- Рівень — 1 + число зв'язків між вузлом і коренем.
- Висота дерева — число ребер найдовшого шляху між коренем і листом.
- Висота вузла — число ребер на найдовшому низхідному шляху від заданого вузла до листа.
- Глибина — число ребер від кореневого вузла дерева до заданого.
- Ліс — набір n ≥ 0 непересічних дерев.
Властивості[ред. | ред. код]
З визначення випливає, що кожна вершина є в свою чергу коренем деякого піддерева. Кількість піддерев вершини має назву ступеня (degree) цієї вершини. Вершина ступеню нуль має назву кінцевої (terminal) або листа (leaf). Некінцева вершина також має назву вершини розгалуження (branch node).
Нехай x — довільна вершина дерева з коренем r. Тоді існує єдиний шлях з r до x. Усі вершини на цьому шляху називаються предками (ancestors) x; якщо деяка вершина y є предком x, то x називається нащадком (descendant) y. Нащадки та предки вершини x, що не збігаються з нею самою, називаються власними нащадками та предками. Кожну вершину x, в свою чергу, можна розглядати як корінь деякого піддерева, елементами якого є вершини-нащадки x.
Якщо вершина x є предком y та не існує вершин поміж ними (тобто x та y з'єднані одним ребром), а також існують предки для x (тобто x не є коренем), то вершина x називається батьком (parent) до y, а y — дитиною (child) x. Коренева вершина єдина не має батьків.
Вершини, що мають спільного батька, називаються братами (siblings). Вершини, що мають дітей, називаються внутрішніми (internal). Глибиною вершини x називається довжина шляху від кореня до цієї вершини. Максимальна глибина вершин дерева називається висотою.
Якщо існує відносний порядок на піддеревах T1…Tm, то таке дерево називається впорядкованим (ordered tree) або пласким (plane tree).
Лісом (англ. forest) називають множину дерев, які не перетинаються.
Найчастіше дерева в інформатиці зображують з коренем, який знаходиться зверху (говорять, що дерево в інформатиці «росте вниз»).
Важливим окремим випадком кореневих дерев є бінарні дерева, які широко застосовуються в програмуванні і визначаються як множина вершин, яка має виокремлений корінь та два піддерева (праве та ліве), що не перетинаються, або є пустою множиною вершин (на відміну від звичайного дерева, яке не може бути пустим).
Піддерева[ред. | ред. код]
Піддерево — частина деревоподібної структури даних, яка може бути представлена у вигляді окремого дерева. Будь-який вузол дерева T разом з усіма його вузлами-нащадками є піддеревом дерева T. Для будь-якого вузла піддерева або має бути шлях в кореневий вузол цього піддерева, або сам вузол повинен бути кореневим. Тобто піддерево пов'язано з кореневим вузлом цілого дерева, а відносини піддерева з усіма іншими вузлами визначаються через поняття відповідне піддерево (за аналогією з терміном «відповідна підмножина»).
Упорядкування дерев[ред. | ред. код]

Існує два основних типи дерев. У рекурсивному або невпорядкованому дереві має значення лише структура самого дерева без урахування порядку нащадків для кожного вузла. Дерево, в якому є заданий порядок (наприклад, кожному ребру, провідному до нащадка, присвоєні різні натуральні числа) називається деревом з іменованими ребрами або впорядкованим деревом зі структурою даних, заданої перед ім'ям. Впорядковані дерева є найбільш поширеними серед деревоподібних структур. Двійкове дерево пошуку — одне з різновидів упорядкованого дерева. Двійкове дерево — структура даних у вигляді дерева, в якому кожна вершина має не більше двох дітей. Зазвичай такі діти називаються правим та лівим. На базі двійкових дерев будуються такі структури, як двійкові дерева пошуку та двійкові купи.
Представлення дерев[ред. | ред. код]
Існує безліч різних способів представлення дерев. Найбільш загальний спосіб представлення зображує вузли як записи, розташовані в динамічно виділеній пам'яті з вказівниками на своїх нащадків, предків (або і тих і інших), або, як елементи масиву, пов'язані між собою відносинами, визначеними їх позиціями в масиві (наприклад, двійкова купа).
Дерева як графи[ред. | ред. код]
В теорії графів, дерево — зв'язний ациклічний граф. Кореневе дерево — це граф з вершиною, виділеною як коренева. У цьому випадку будь-які дві вершини, пов'язані ребром, успадковують відносини «батько-нащадок». Незв'язний граф, що складається виключно з дерев, називається лісом.
Методи обходу[ред. | ред. код]
Покроковий перебір елементів дерева по зв'язкам між вузлами-предками і вузлами-нащадками називається обходом дерева. Найчастіше, операція може бути виконана переходами вказівника на окремі вузли. Обхід, при якому кожен вузол-предок проглядається раніше його нащадків називається предвпорядкованим обходом або обходом в прямому порядку (pre-order walk), а коли проглядаються спочатку нащадки, а потім предки, то обхід називається післявпорядкованим обходом або обходом у зворотному порядку (post-order walk). Існує також симетричний обхід, при якому відвідується спочатку ліве піддерево, потім вузол, потім — праве піддерево, і обхід в ширину, при якому вузли відвідуються рівень за рівнем (N-й рівень дерева — безліч вузлів з висотою N). Кожен рівень обходиться зліва направо.
Обхід бінарного дерева передбачає відвідування усіх вершин бінарного дерева, при цьому кожна з вершин відвідується тільки один раз. Існують три види таких обходів, кожний з яких визначається рекурсивно:
- прямий порядок (англ. preorder) наступної послідовності:
- відвідати корінь
- відвідати ліве піддерево
- відвідати праве піддерево
- Тобто, в такому порядку обходу кожна вершина відвідується до того, як будуть відвідані її діти.
- зворотний порядок (англ. postorder) наступної послідовності:
- Тобто, в такому порядку кожна вершина відвідується лише після того, як будуть відвідані її діти.
- центрований (центральний) порядок (англ. inorder) наступної послідовності:
- відвідати ліве піддерево
- відвідати корінь
- відвідати праве піддерево
- В такому порядку кожна вершина відвідується між відвіданням лівої та правої дитини. Такий порядок особливо часто застосовується в бінарних деревах пошуку, тому що дає можливість обходу вершин у порядку збільшення їхніх порядкових номерів.
|
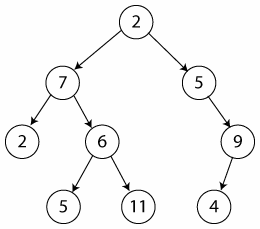
Для цього бінарного дерева,
- Прямий порядок: 2, 7, 2, 6, 5, 11, 5, 9, 4
- Зворотний порядок: 2, 5, 11, 6, 7, 4, 9, 5, 2
- Центрований (центральний) порядок: 2, 7, 5, 6, 11, 2, 5, 4, 9
Операції над деревом[ред. | ред. код]
- обхід вершин в різному порядку
- перенумерація вершин
- пошук елемента
- додавання елемента у визначене місце в дереві
- видалення елемента
- видалення цілого фрагмента дерева
- додавання цілого фрагмента дерева
- трансформації (повороти) фрагментів дерева
- знаходження кореня для будь-якої вершини
Найбільшого розповсюдження ці структури даних набули в тих задачах, де необхідне маніпулювання з ієрархічними даними, ефективний пошук в даних, їхнє структуроване зберігання та модифікація.
Загальне застосування[ред. | ред. код]
- управління ієрархією даних;
- спрощення пошуку інформації (див. обхід дерева);
- управління сортованими списками даних;
- синтаксичний аналіз виразів (англ. parsing), оптимізація програм;
- як технологія компонування цифрових зображень для отримання різних візуальних ефектів;
- форма прийняття багатоетапного рішення (див. ділові шахи).
Див. також[ред. | ред. код]
- Дерево (теорія графів)
- Бінарне дерево
- Бінарне дерево пошуку
- Збалансоване дерево
- B-дерево
- AVL-дерево
- Червоно-чорне дерево
- Обхід дерева
- Розширюване дерево
- Деревна глибина (теорія графів)
Джерела[ред. | ред. код]
- Дональд Кнут, Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. ISBN 0-201-89683-4
| Цю статтю треба вікіфікувати для відповідності стандартам якості Вікіпедії. (січень 2013) |
| |||||||||||||||||
- ↑ Дерево // Словник української мови : у 20 т. — К. : Наукова думка, 2010—2022.