Комірки Бенара
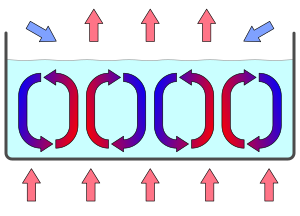
Комірки Бенара або Релея — Бенара — упорядковані конвективні осередки у формі циліндричних валів або правильних шестигранних структур в шарі в'язкої рідини з вертикальним градієнтом температури, тобто в середовищі з рівномірним підігрівом знизу.
Комірки Релея — Бенара є одним із трьох стандартних прикладів самоорганізації, поряд із лазером і реакцією Бєлоусова — Жаботинського.
Керівним параметром самоорганізації служить градієнт температури. Внаслідок підігріву в спочатку однорідному шарі рідини починається дифузія, внаслідок чого виникають неоднорідності щільності. При подоланні деякого критичного значення градієнту, дифузія не встигає привести до однорідного розподілу температури в об'ємі. Виникають циліндричні вали, що обертаються назустріч один одному (як зчеплені шестерні)[1]. При збільшенні градієнту температури виникає другий критичний перехід. Для прискорення дифузії кожен вал розпадається на два вали меншого розміру. При подальшому збільшенні керуючого параметра вали дробляться і в межі виникає турбулентний хаос, що чітко видно на біфуркаційній діаграмі або дереві Фейгенбаума.
У тонкому шарі при підігріві знизу утворюються комірки правильної гексагональної форми, усередині яких рідина підіймається в центрі й опускається гранями комірки[2]. Така постановка експерименту історично була першою, однак тут насправді спостерігається конвекція Марангоні, що виникає за рахунок дії сил поверхневого натягу і залежності їх від температури рідини.
Важливим у задачі про конвекцію в плоскому шарі є той факт, що для запису її в наближенні Бусінеска можливо отримати точний аналітичний розв'язок рівнянь гідродинаміки. Правда, простий точний розв'язок вдається знайти лише при абстрактній постановці з двома вільними недеформованими межами шару (як зверху, так і знизу), реалістичніші варіанти таких розв'язків не мають (але для них добре працюють наближені аналітичні методи, наприклад метод Гальоркіна).
Наведемо тут розв'язок задачі[3][4]. Приймемо, що вісь z спрямована вгору, перпендикулярно до шару, осі x і y паралельні границям. Початок координат зручно вибрати на нижній межі шару. Вихідні рівняння конвекції:
Безрозмірна форма рівнянь конвекції для малих збурень рівноваги, в припущенні експоненціального зростання збурень у часі (т. з. «нормальні» обурення) — :
де — одиничний вектор осі z, — відповідно число Прандтля та число Релея, — інкремент наростання (швидкість росту) збурень. Після обезрозмірювання змінна z змінюється від 0 до 1. Так звані «нормальні» збурення є частковими розв'язками лінійної системи диференціальних рівнянь, і тому знаходять широке застосування при дослідженні задач у дуже різних областях.
Постановка граничних умов робиться в припущенні, що обидві границі не деформуються, але вільні — при цьому відсутні дотичні напруження в рідині. Граничні умови:
- , — недеформованість границь.
, — відсутність дотичних напружень. Оскільки вважаємо, що працюємо з рідиною, для якої справедливо рівняння Нав'є-Стокса, то можемо явно записати вигляд тензора в'язких напруг і отримати граничні умови для компонент швидкості.
- — закон Нав'є,
Приймаючи позначення для компонент швидкості: , перепишемо граничну умову для дотичних напружень у термінах швидкості:
- .
Для збурень температури на границях приймається нульове значення. У результаті, система граничних умов завдання така:
Тепер, припускаючи збурення нормальними по простору — (тут — хвильовий вектор збурення, паралельний площині ) і замінюючи оператори диференціювання — , можемо переписати систему рівнянь конвекції у вигляді системи звичайних диференціальних рівнянь:
Взявши подвійний ротор від першого рівняння і спроектувавши його на вісь z, отримаємо остаточну систему рівнянь для збурень:
Виходячи з граничних умов, а також з того, що всі похідні в системі парного порядку, зручно представити рішення у вигляді тригонометричних функцій:
де n — ціле число. Рішення у вигляді синусів задовольняє одразу всім граничним умовам.

Далі, позначаючи , і підставляючи передбачуваний вид розв'язку в рівняння, отримаємо лінійну однорідну алгебраїчну систему для a, b. З її визначника можна виразити залежність :
Приймаючи тут — границя монотонної стійкості, незростання нормальних збурень — отримаємо формулу для визначення критичного числа Релея n-ї моди збурень:
Найменше число Релея вийде при . Мінімум залежності, як нескладно переконатися, припадає на , а мінімальне число Релея дорівнює . Згідно з критичним хвильовим числом у шарі виникають структури у вигляді валів ширини (у безрозмірних одиницях).
Для задач з іншими варіантами границь критичне число Релея виявляється вищим. Наприклад, для шару з двома твердими межами воно дорівнює 1708 [5], для шару з твердою верхньою та нижньою вільною межами — 1156, змінюються і критичні хвильові числа. Однак якісно картина конвективних валів не змінюється.
- ↑ Ван-Дайк М. Альбом течений жидкости и газа, М.: Мир, 1986 — c. 84, рис. 139—140
- ↑ Ван Дайк-М. Альбом течій рідини і газу, М.: Світ, 1986 — c. 85, рис. 140—141
- ↑ Гершуни Г. З., Жуховицкий Е. М. Конвективная устойчивость несжимаемой жидкости. // М.: Наука, 1972 — § 5
- ↑ Фрик П. Г. Турбулентность: методы и подходы. Курс лекций, ч.1 // Пермь: Пермский гос. техн. ун-т., 1998 — с. 33-37
- ↑ Гершуни Г. З., Жуховицкий Е. М., там же, § 6




































