Інтерферометричний радар з синтезованою апертурою
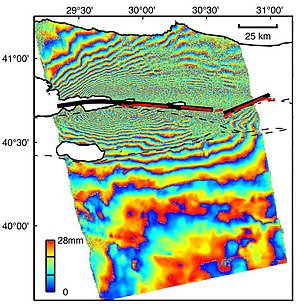
Інтерферометричний радар з синтезованою апертурою, скорочено InSAR (або застарілий IfSAR ), — це радіолокаційна технологія, який використовується в геодезії та дистанційному зондуванні. Цей геодезичний метод використовує два або більше зображення радару із синтезованою апертурою (SAR) для створення карт деформації поверхні або цифрової моделі місцевості, використовуючи різницю у фазі хвиль, що повертаються до супутника [1] [2] [3] або літака. Ця техніка може вимірювати деформації масштабу до міліметрів за період від декількох днів до кількох років. Його можна застосувати для геофізичного моніторингу природних небезпек, наприклад, землетрусів, вулканів і зсувів, а також у будівельній інженерії, зокрема моніторингу осідання та структурної стійкості.
Радар із синтетичною апертурою (SAR) — це форма радару, який використовує складне оброблення радіолокаційних даних для створення дуже вузького ефективного променя. Його можна використовувати для формування зображень відносно нерухомих цілей; зображення рухомих об'єктів можуть бути розмиті або зсунуті. SAR є формою активного дистанційного зондування – антена передає випромінювання, яке відбивається від області зображення, на відміну від пасивного зондування, де випромінювання відбувається за рахунок навколишнього освітлення. За рахунок чого, отримання зображень SAR не залежить від природного освітлення, і зображення можна робити вночі. Радар використовує електромагнітне випромінювання на мікрохвильових частотах; поглинання атмосферою на типових радіолокаційних довжинах хвиль дуже низьке, тому хмарний покрив не перешкоджає спостереженням.

SAR використовує амплітуду та абсолютну фазу даних з поверненого сигналу. На відміну від цього, інтерферометрія використовує диференціальну фазу відбитого випромінювання або від кількох проходів уздовж однієї траєкторії та/або з декількох зміщених фазових центрів (антен) під час одного проходу. Оскільки вихідна хвиля створюється супутником, фаза відома, і її можна порівняти з фазою поверненого сигналу. Фаза зворотної хвилі залежить від відстані до землі, оскільки довжина шляху до землі та назад складатиметься з кількох цілих довжин хвиль, а також певної частини довжини хвилі. Це спостерігається як різниця фаз або фазовий зсув у зворотній хвилі. Загальна відстань до супутника (тобто кількість цілих довжин хвиль) відома на основі часу, необхідного для проходження відстані до супутника, але саме додаткова частина довжини хвилі особливо цікава, тому вимірюється з високою точністю.
На практиці фаза поверненого сигналу піддається впливу декількох факторів, які разом створюють похибку, що робить дані SAR фактично довільними, без кореляції від пікселя до пікселя. Щоб отримати будь-яку корисну інформацію з фази, деякі з цих ефектів повинні бути виділені та видалені. Інтерферометрія використовує два зображення однієї і тієї ж області, отримані з однієї позиції (або, для топографічних застосувань, з дещо різних позицій) і знаходить різницю фаз між ними, створюючи зображення, відоме як інтерферограма. Різниця фаз вимірюється в радіанах і, через циклічну природу фази, записується як повторювані смуги, кожна з яких представляє повний цикл 2π.
Найбільш важливим та вагомим фактором, який впливає на фазу, є взаємодія з поверхнею землі. Фаза хвилі може змінюватися при відбиванні від матеріалу в залежності від його властивостей. Відбитий сигнал з кожного пікселя є сумарним внеском у фазу від багатьох менших «цілей» в тій області землі, кожна з яких має різні діелектричні властивості та відстань від супутника, що означає, довільність повернутого сигналу, який не корелює з сусідніми пікселями . Однак, важливим є те, що він є послідовним – за умови, що на землі нічого не змінюється, внески від кожної цілі повинні кожного разу підсумовуватися однаково, і, отже, бути видалені з інтерферограми.
Одного разу, коли ефекти ґрунту були видалені, головним сигналом, присутнім у інтерферограмі, став внесок орбітальних ефектів. Щоб інтерферометрія працювала, супутники повинні бути якомога ближче до однієї просторової позиції під час отримання зображень. Це означає, що зображення з двох супутникових платформ з різними орбітами не можуть бути порівняні, і для даного супутника потрібно використовувати дані з однієї і тієї ж орбітальної траси. На практиці перпендикулярна відстань між ними, відома як базова лінія, часто відома з точністю до кількох сантиметрів, але її можна контролювати лише в масштабі від десятків до сотень метрів. Ця невелика різниця спричиняє регулярну різницю у фазі, яка плавно змінюється по всій інтерферограмі та може бути змодельована та видалена.

Незначна різниця в положенні супутника також вносить похибку, що спричинена топографією, тобто стереоскопічний ефект створює додаткову різницю у фазі. Чим довша базова лінія, тим менша топографічна висота необхідна для створення смуги зміни фази – відомої як висота неоднозначності . Цей ефект можна використати для розрахунку топографічної висоти та створення цифрової моделі рельєфу (ЦМР).
Якщо висота топографії вже відома, внесок топографічної фази можна обчислити та видалити. Традиційно це робиться двома способами. У методі двох проходів використовується інформація про висоту із зовнішньої ЦММ разом з інформацією про орбіту для розрахунку внеску фази. У методі трьох проходів два знімки, зроблені з коротким проміжком часу, використовуються для створення інтерферограми, яка, як припускається, не має сигналу деформації та представляє топографічний внесок. Ця інтерферограма потім віднімається від третього знімка з більшим часовим проміжком, щоб отримати залишкову фазу, пов'язану з деформацією.
- ↑ Massonnet, D.; Feigl, K. L. (1998), Radar interferometry and its application to changes in the earth's surface, Rev. Geophys., 36 (4): 441—500, Bibcode:1998RvGeo..36..441M, doi:10.1029/97RG03139
- ↑ Burgmann, R.; Rosen, P.A.; Fielding, E.J. (2000), Synthetic aperture radar interferometry to measure Earth's surface topography and its deformation, Annual Review of Earth and Planetary Sciences, 28: 169—209, Bibcode:2000AREPS..28..169B, doi:10.1146/annurev.earth.28.1.169
- ↑ Hanssen, Ramon F. (2001), Radar Interferometry: Data Interpretation and Error Analysis, Kluwer Academic, ISBN 9780792369455