Теорема про рівні вписані кола

Якщо сині кола рівні, то зелені кола також рівні.

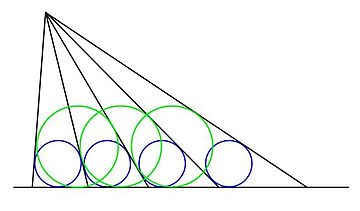
Теорема про рівні вписані кола бере початок у японських сангаку і стосується такої побудови: серія променів проводиться з якоїсь точки до перетину з заданою прямою так, що кола, вписані в трикутники, утворені суміжними променями і прямою, однакові. На ілюстрації однакові сині кола визначають кути між променями, як описано вище.

Формулювання теореми

Теорема стверджує, що за описаної вище побудови кола, вписані в трикутники, утворені променями через один (тобто отримані об'єднанням двох сусідніх трикутників), через два і т. д., також рівні. Випадок сусідніх трикутників показано на малюнку зеленими колами: всі вони однакові.

З факту, що твердження теореми не залежить від кута між початковим променем і заданою прямою, можна зробити висновок, що теорема скоріше належить до математичного аналізу, а не геометрії, і повинна мати стосунок до неперервної маштабної функції, яка визначає відстань між променями. Фактично цією функцією є гіперболічний синус.

Лема

Теорема є прямим наслідком такої леми.

Припустимо, що n-й промінь утворює з нормаллю до базової прямої кут $\gamma _{n}$. Якщо $\gamma _{n}$ параметризовано відповідно до рівності $\mathrm {tg} \,\gamma _{n}=\mathrm {sh} \,\theta _{n}$, то значення $\theta _{n}=a+nb$, де $a$ і $b$ — дійсні сталі, визначають послідовність променів, які задовольняють умовам вписаних кіл (див. вище), і щобільше, будь-яку послідовність променів, що задовольняють цим умовам, можна отримати належним вибором параметрів $a$ і $b$.

Доведення леми

На малюнку суміжні промені PS і PT утворюютьють з прямою PR, перпендикулярною до базової прямої RT, кути $\gamma _{n}$ і $\gamma _{n+1}$.

Проведемо через центр O вписаного в трикутник $\triangle$ PST кола пряму QY, паралельну до базової прямої. Це коло дотикається до променів у точках W і Z. відрізок PQ має довжину $h-r$, а відрізок QR має довжину $r$, що дорівнює радіусу вписаного кола.

Тоді $\triangle$ OWX подібний $\triangle$ PQX, $\triangle$ OZY подібний $\triangle$ PQY, а з XY = XO + OY ми отримуємо

$(h-r)(\mathrm {tg} \,\gamma _{n+1}-\mathrm {tg} \,\gamma _{n})=r(\sec \gamma _{n}+\sec \gamma _{n+1}).$

Це відношення на множині кутів $\{\gamma _{m}\}$ виражає умову рівності вписаних кіл.

Для доведення леми покладемо $\mathrm {tg} \,\gamma _{n}=\mathrm {sh} \,(a+nb)$. Цей вираз можна перетворити на $\sec \gamma _{n}=\mathrm {ch} \,(a+nb)$.

Використовуючи рівність $a+(n+1)b=(a+nb)+b$, застосовуємо додаткові правила для $\mathrm {sh} \,$ і $\mathrm {ch} \,$ і перевіряємо, що відношення рівності кіл задовольняється виразом

${\frac {r}{h-r}}=\mathrm {th} \,{\tfrac {b}{2}}.$

Ми отримали вираз для параметра $b$ в термінах геометричних величин $h$ і $r$. Далі, визначаючи $b$, отримуємо вираз для радіусів $r_{N}$ вписаних кіл, утворених вибором кожного N-го променя стороною трикутника:

${\frac {r_{N}}{h-r_{N}}}=\mathrm {th} \,{\tfrac {Nb}{2}}.$

Див. також

• Японська теорема про вписані в коло многокутники
• Японська теорема про вписаний чотирикутник

Література

• Tabov J. A note on the five-circle theorem [Архівовано 2 травня 2021 у Wayback Machine.] // Mathematics Magazine. — 1989. — Т. 63. — № 2. — С. 92-94.