Користувач:SemenjukSergiy/Практичне число

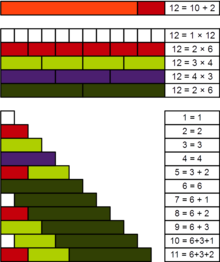
Практичне число 12

Практичне число або панарітмічне число - це додатне ціле число n, таке що все менші додатні цілі числа можуть бути представлені у вигляді суми різних дільників числа n. Наприклад, 12 є практичним числом, оскільки всі числа від 1 до 11 можна представити у вигляді суми дільників 1, 2, 3, 4 і 6 цього числа - крім самих подільників, ми маємо 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1 і 11 = 6 + 3 + 2.

Послідовність практичних чисел (послідовність A005153 з Онлайн енциклопедії послідовностей цілих чисел, OEIS ) починається з

1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140, 144, 150. . . .

Практичні числа використовував Фібоначчі в своїй книзі Liber Abaci (1202) у зв'язку з завданням подання раціональних чисел у вигляді єгипетських дробів . Фібоначчі не визначав формально практичні числа, але він дав таблицю подання єгипетських дробів для дробів з практичними знаменниками .

Назва «практичне число» дав Шрінівасан . Він зауважив, що «розбиття грошей, ваги та інших заходів, що використовують числа, такі як 4, 12, 16, 20 і 28, які зазвичай так незручні, що заслуговують заміни на ступені 10.» Він перевідкрив ряд теоретичних властивостей таких чисел і першим спробував класифікувати ці числа, а Стюарт і Серпінський завершили класифікацію. Визначення практичних чисел уможливлює визначити, чи є число практичним шляхом перегляду розкладу числа на прості множники. Будь-яке парне досконале число і будь-яка степень двійки [en] є практичним числом.

Можна показати, що практичні числа аналогічні простим числам у багатьох відношеннях .

Опис практичних чисел

Початковий опис Шрінівасана стверджує, що практичне число не може бути недостатнім числом, це число, сума всіх дільників якого (включаючи 1 і саме число) менше подвоєного числа, якщо не брати до уваги нестачу, що дорівнює одиниці. Якщо для практичного числа $n$ виписати впорядкована множина дільників ${d_{1},d_{2},...,d_{j}}$, де $d_{1}=1$ і $d_{j}=n$, То твердження Шрінівасан можна виразити нерівністю

$2n\leqslant 1+\sum _{i=1}^{j}d_{i}$ .

Іншими словами, упорядкована послідовність всіх дільників ${d_{1}<d_{2}<...<d_{j}}$ практичного числа повинна бути повною підпослідовність .

Це визначення розширили і завершили Стюарт і Серпінський , які показали, що визначення, чи є число практичним, визначається його розкладанням на прості подільники . Позитивне ціле число, більше одиниці з розкладанням $n=p_{1}^{\alpha _{1}}...p_{k}^{\alpha _{k}}$ (з сортуванням простих дільників по зростанню $p_{1}<p_{2}<\dots <p_{k}$ ), є практичним тоді і тільки тоді, коли кожен його простий дільник $p_{i}$ досить малий, щоб $p_{i}-1$ мало подання у вигляді суми менших дільників. Щоб це було вірно, перше просте число $p_{1}$ має дорівнювати 2, а для будь-якого i від 2 до k для кожного наступного простого числа $p_{i}$ має виконуватися нерівність

$p_{i}\leqslant 1+\sigma (p_{1}^{\alpha _{1}}p_{2}^{\alpha _{2}}\dots p_{i-1}^{\alpha _{i-1}})=1+\prod _{j=1}^{i-1}{\frac {p_{j}^{\alpha _{j}+1}-1}{p_{j}-1}},$

де $\sigma (x)$ означає суму дільників числа x. наприклад, $2\times 3^{2}\times 29\times 823=429606$ є практичним, оскільки нерівність виконується для кожного простого дільника: $3\leqslant \sigma (2)+1=4,29\leqslant \sigma (2\times 3^{2})+1=40$ і $823\leqslant \sigma (2\times 3^{2}\times 29)+1=1171$ .

Умова, наведена вище, є необхідною і достатньою. В одному напрямку, ця умова є необхідною, щоб можна було уявити $p_{i}-1$ у вигляді суми дільників числа n, оскільки в разі порушення нерівності складання всіх менших дільників дало б суму, занадто маленьку, щоб отримати $p_{i}-1$ . В іншому напрямку, умова є достатньою, що можна отримати за індукцією. Більш строго, якщо розкладання числа n задовольняє вищенаведені умові, то будь-яке число $m\leqslant \sigma (n)$ може бути представлено у вигляді суми дільників числа n після наступних кроків  :

• нехай $q=\min\{\lfloor m/p_{k}^{\alpha _{k}}\rfloor ,\sigma (n/p_{k}^{\alpha _{k}})\}$, і нехай $r=m-qp_{k}^{\sigma _{k}}$ .
• З огляду на, що можна показати по індукції, що $q\leqslant \sigma (n/p_{k}^{\alpha _{k}})$ і $n/p_{k}^{\alpha _{k}}$ є практичними, ми можемо знайти подання q у вигляді суми дільників $n/p_{k}^{\alpha _{k}}$ .
• З огляду на, що можна показати по індукції, що $r\leqslant \sigma (n)-p_{k}^{\alpha _{k}}\sigma (n/p_{k}^{\alpha _{k}})=\sigma (n/p_{k})$ і $n/p_{k}$ є практичними, ми можемо знайти подання r у вигляді суми дільників $n/p_{k}$ .
• Подання у вигляді подільників r, разом з коефіцієнтом $p_{k}^{\alpha _{k}}$ для кожного дільника подання у вигляді подільників q, разом утворюють подання m у вигляді суми дільників n.

Властивості

• Єдине непарне практичне число - 1, оскільки якщо n> 2 є непарним числом, то 2 можна представити у вигляді суми різних дільників числа n. Шрінівасан зауважив, що відмінні від 1 і 2 практичні числа діляться на 4 або 6 (або на обидва).
• Добуток двох практичних чисел є також практичним числом . Більш сильне твердження, найменше спільне кратне будь-яких двох практичних чисел, є також практичним числом. Еквівалентно, множина всіх практичних чисел замкнуто по множенню.
• З опису чисел Стюартом і Серпінським можна бачити, що в разі, коли n є практичним числом, а d є одним з його подільників, число n * d має бути також практичним числом.
• У множині всіх практичних чисел існує множина простих практичних чисел. Просте практичне число - це або практичне і вільне від квадратів число, або практичне і при розподілі на будь-який його простий дільник, показник якого в розкладанні більше 1, перестає бути практичним. Послідовність простих практичних чисел послідовність A267124 з Онлайн енциклопедії послідовностей цілих чисел, OEIS ) починається з

1, 2, 6, 20, 28, 30, 42, 66, 78, 88, 104, 140, 204, 210, 220, 228, 260, 272, 276, 304, 306, 308, 330, 340, 342, 348, 364, 368, 380, 390, 414, 460. . .

Зв'язок з іншими класами чисел

Кілька інших гідних уваги множин цілих чисел складаються виключно з практичних чисел:

• З властивостей, наведених вище, для практичного числа n і одного з його подільників d (тобто, d | n) число n * d має також бути практичним, так що помножена на 6 будь-який степінь числа 3 повинна бути практичним числом, як і помножена на 6 будь-який степінь числа 2.
• Будь-яка степень двійки [en] є практичним числом . Ступінь двійки тривіально задовольняє опису практичних чисел в термінах розкладання цілих чисел - всі прості числа в розкладанні числа, p _1, дорівнюють двом, що і потрібно.
• Будь-яке парне досконале число є також практичним числом . Це випливає з результату Ейлера, що парне досконале число має мати вигляд $2^{n-1}(2^{n}-1)$ . Непарна частина цього розкладання дорівнює сумі дільників парної частини, так що будь-який непарний простий дільник такого числа повинен бути не більше суми дільників парної частини числа. Таким чином, це число має задовольняти опису практичних чисел.
• Будь прайморіал (добуток перших i простих для деякого числа i) є практичним числом . Для перших двох прайморіалов, двійки і шістки це ясно. Кожен наступний прайморіал утворюється множенням простого числа p _i на менший прайморіал, який ділиться як на двійку, так і на попереднє просте число $p_{i-1}$ . Згідно постулату Бертрана $p_{i}<2p_{i-1}$, так що кожен попередній простий дільник прайморіала менше, ніж один з дільників попереднього прайморіала. За індукцією, з цього випливає, що будь-який прайморіал задовольняє опису практичних чисел. Оскільки прайморіал за визначенням вільний від квадратів, він також є простим практичним числом.
• Узагальнюючи прайморіали, будь-яке число, яке є добутком ненульових ступенів перших k простих чисел, має бути практичним. У цю множину потрапляють надскладові числа Рамануджана (числа з кількістю дільників, великим будь-якого меншого позитивного числа), а також факторіали .

Практичні числа і єгипетські дроби

Якщо n є практичним, то будь-який раціональне число виду m / n з m <n може бути представлений у вигляді суми $\sum {\tfrac {d_{i}}{n}}$, Де все d _i є різними дільниками числа n. Кожен член в цій сумі приводиться до аліквотного дробу, так що така сума дає подання числа m / n у вигляді єгипетської дробу . наприклад,

${\frac {13}{20}}={\frac {10}{20}}+{\frac {2}{20}}+{\frac {1}{20}}={\frac {1}{2}}+{\frac {1}{10}}+{\frac {1}{20}}.$

Фібоначчі в своїй книзі 1202 року Liber Abaci наводить деякі методи пошуку подання раціонального числа у вигляді єгипетської дробу. З них перший метод полягає в перевірці, чи не є число вже аліквотним дробом, а другий метод полягає в поданні чисельника у вигляді суми дільників знаменника, як описано вище. Це метод гарантує успіх тільки в разі, коли знаменник є практичним числом. Фібоначчі привів таблиці таких поданнь для дробів, що мають в якості знаменників практичні числа 6, 8, 12, 20, 24, 60 і 100.

Воуз показав, що будь-яке число x / y має подання у вигляді єгипетської дробу з $\scriptstyle O({\sqrt {\log y}})$ членами. Доведення використовує пошук послідовності практичних чисел n _i з властивістю, що будь-яке число, менше n _i, може бути записано у вигляді суми $\scriptstyle O({\sqrt {\log n_{i-1}}})$ різних дільників числа n _i. Тоді i вибирається так, що $n_{i-1}<y\leqslant n_{i}$ і $xn_{i}$ ділиться на y, даючи частку q і залишок r. З цього вибору випливає, що $\scriptstyle {\frac {x}{y}}={\frac {q}{n_{i}}}+{\frac {r}{yn_{i}}}$ . Розклавши чисельники в правій частині формули на суму дільників числа n _i одержимо подання числа у вигляді єгипетської дробу. Тененбаум і Йокота використовували подібну техніку, що використовуючи іншу послідовність практичних чисел, щоб показати, що будь-яке число x / y має подання у вигляді єгипетської дробу, в якій найбільший знаменник дорівнює $\scriptstyle O({\frac {y\log ^{2}y}{\log \log y}})$ .

Згідно вересневої 2015 року гіпотезі Чжи-Вей Сунь будь-яке позитивне раціональне число має подання у вигляді єгипетської дробу, в якому будь-який знаменник є практичним числом. Існує доказ гіпотези в блозі Девіда Еппштейна .

Аналогія простим числам

Одна з причин інтересу до практичних чисел полягає в тому, що багато хто з їх властивостей подібні властивостями простих чисел . Більш того, теореми, аналогічні гіпотезі Гольдбаха і гіпотезі про числа-близнюки, відомі для практичних чисел - будь-яке позитивне парне число є сумою двох практичних чисел і існує нескінченно багато трійок практичних чисел $x-2,x,x+2$ . Джузеппе Мелфі показав також, що існує нескінченно багато практичних чисел Фібоначчі (послідовність A005153 з Онлайн енциклопедії послідовностей цілих чисел, OEIS). Аналогічне питання про існування нескінченного числа простих чисел Фібоначчі [en] залишається відкритим. Хаусман і Шапіро показали, що існує завжди практичне число в інтервалі $[x_{2},(x+1)^{2}]$ для будь-якого додатнього дійсного x, що є аналогом гіпотези Лежандра для простих чисел.

Нехай p (x) підраховує кількість практичних чисел, що не перевершують x. Маргенштерн висловив гіпотезу, що p (x) асимптотично дорівнює cx/log x для деякої константи c, що нагадує формулу в теоремі про розподіл простих чисел і підсилює більш раннє твердження Ердеша і Локстона , що практичні числа мають щільність нуль в множині цілих чисел. Сайес довів, що для відповідних констант c ₁ і c ₂

$c_{1}{\frac {x}{\log x}}<p(x)<c_{2}{\frac {x}{\log x}},$

Нарешті, Вайнгартнер довів гіпотезу Маргенштерна, показавши, що

$p(x)={\frac {cx}{\log x}}\left(1+O\!\left({\frac {\log \log x}{\log x}}\right)\right),$

для $x\geqslant 3$ і деякої константи $c>0$ .

Література

• Paul Erdős, Loxton J. H.  // Journal of the Australian Mathematical Society (Series A). — 1979. — Вип. 03. — С. 319–331.
• Heyworth M. R.  // New Zealand Math. Mag.. — 1980. — Вип. 1. — С. 24–28.. Как процитировано у Маргенштерна (Margenstern, 1991).
• Miriam Hausman, Harold N. Shapiro.  // Communications on Pure and Applied Mathematics. — 1984. — Вип. 5. — С. 705–713.
• Maurice Margenstern.  // Comptes Rendus de l'Académie des Sciences, Série I. — 1984. — Вип. 18. — С. 895–898. Как процитировано у Маргенштерна (Margenstern, 1991).
• Maurice Margenstern.  // Journal of Number Theory. — 1991. — Вип. 1. — С. 1–36.
• Giuseppe Melfi.  // Journal of Number Theory. — 1996. — Вип. 1. — С. 205–210.
• Dragoslav S. Mitrinović, József Sándor, Borislav Crstici. III.50 Practical numbers // {{{Заголовок}}}. — Kluwer Academic Publishers, 1996. — С. 118–119. — (Mathematics and its Applications) — ISBN 978-0-7923-3823-9.
• Robinson D. F.  // New Zealand Math. Mag.. — 1979. — Вип. 2. — С. 47–52.. Как процитировано у Маргенштерна (Margenstern, 1991) и Митриновича Mitrinović, Sándor та Crstici, (1996).
•  // Journal of Number Theory. — 1997. — Вип. 1. — С. 163–191.
• {{{Заголовок}}} / Laurence E. Sigler (перевод). — Springer-Verlag, 2002. — С. 119–121. — ISBN 0-387-95419-8.
• Wacław Sierpiński.  // Annali di Matematica Pura ed Applicata. — 1955. — Вип. 1. — С. 69–74.
• Srinivasan A. K.  // Current Science. — 1948. — С. 179–180.
• Stewart B. M.  // American Journal of Mathematics. — The Johns Hopkins University Press, 1954. — Вип. 4. — С. 779–785.
• Tenenbaum G., Yokota H.  // Journal of Number Theory. — 1990. — Вип. 2. — С. 150–156.
• Vose M.  // Bulletin of the London Mathematical Society. — 1985. — Вип. 1. — С. 21.
• Weingartner A.  // The Quarterly Journal of Mathematics. — 2015. — Вип. 2. — С. 743–758.

Посилання

• Tables of practical numbers compiled by Giuseppe Melfi.
• Practical Number на PlanetMath.(англ.)
• Weisstein, Eric W. Practical Number(англ.) на сайті Wolfram MathWorld.

[[Категорія:Цілочисельні послідовності]]