Детермінований хаос

Детерміно́ваний хао́с — хаотична поведінка детерміністичної системи, яка проявляється через надзвичайно високу чутливість до початкових умов. Явище детермінованого хаосу неодноразово спостерігалося як в лабораторних умовах (в плазмі, електричних колах, лазерах, хімічних реакціях, рідинах, в низці механічних пристроїв) так і в природі (динаміка зростання популяцій та метеорологічні явища). Першими дослідниками хаосу були французькі математики Анрі Пуанкаре та Жак Адамар. Термін «хаос» увів в обіг американський математик Джеймс Йорк в 1975 році.

Визначення

Еволюція детерміністичної системи характеризується тим, що для будь-якого початкового стану системи в момент часу $t_{0}$ однозначно визначений стан в момент часу $t>t_{0}$. Якщо характеризувати систему певним набором змінних $\mathbf {x} (t)$, то математично еволюцію системи можна записати

$\mathbf {x} (t)={\hat {S}}(t,t_{0})\mathbf {x} (t_{0})$,

де ${\hat {S}}$ — оператор еволюції.

Проте, детермінованість еволюції не означає її стійкості. Якщо розглянути два початкові стани $\mathbf {x} _{1}$ i $\mathbf {x} _{2}$, які дуже близькі один до одного, то стани ${\hat {S}}(t,t_{0})\mathbf {x} _{1}$ і ${\hat {S}}(t,t_{0})\mathbf {x} _{2}$ не обов'язково будуть близькими.

Детермінований хаос виникає тоді, коли результати еволюції, що починаються із нескінченно малого околу певної початкової точки, покривають скінченну область у фазовому просторі, тобто коли незначне відхилення у початкових умовах призводить до значного відхилення в кінцевій точці.

Найпростішою неперервною системою, в якій спостерігається детермінований хаос, є дивний атрактор Лоренца.

Біфуркаційна діаграма для відображення повернення, що демонструє наростання хаотичної поведінки із зміною параметру.

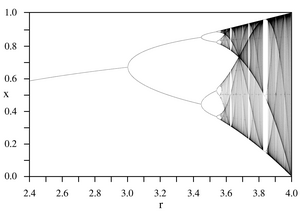
У системах, що описуються нелінійними диференційними рівняннями, обов'язкою умовою існування детермінованого хаосу є вимога того, щоб система описувалася принаймні трьома динамічними змінними. У двовимірному випадку неможливо побудувати фазовий портрет системи, в якому фазові траєкторії не перетиналися б (вимога детермінізму) й існував хаос. У системах із дискретним часом такої вимоги не існує. Наприклад, хаос виникає в одновимірній задачі про відображення повернення, яка визначається рівнянням:

$x_{n+1}=Rx_{n}(1-x_{n})$.

Історія

В основу теорії хаосу лягли, серед інших, роботи Анрі Пуанкаре, Едварда Лоренца, Бенуа Мандельброта, Бориса Чирікова, Якова Синая та Мітчела Файгенбаума.

Першовідкривачем хаосу вважають Анрі Пуанкаре. Під час дослідження задачі трьох тіл він встановив існування траєкторій, які не є періодичними, не зростають безмежно і не прямують до якоїсь фіксованої точки. В 1898 році Жак Адамар показав, що динаміка частинки, що котиться без тертя вздовж поверхні з негативною кривизною є хаотичною, тобто всі траєкторії частинки є нестійкими і екпоненційно розбігаються з плином часу. Детальніше див. Більярд Адамара

Розвиток теорії детермінованого хаосу значно прискорився після винаходу комп'ютерів. В 1963 американський фізик Едвард Лоренц опублікував свої чисельні дослідження термічної конвекції в яких спостерігалася надзвичайна чутливість системи до початкових умов.

Значимість та застосування

Існування детермінованого хаосу накладає обмеження на можливість моделювання складних процесів, наприклад, метеорологічних. Довготермінове прогнозування погоди стає неможливим не тому, що математичні моделі, які при цьому використовуються, обмежені, а тому, що найменша похибка в зібраних даних із необхідністю призводить до зовсім неправильного результату.

Див. також

• Ефект метелика

Література

• Сугаков В. Й. Основи синерґетики. — К. : Обереги, 2001. — 287 с.
• Глосарій термінів з хімії // Й.Опейда, О.Швайка. Ін-т фізико-органічної хімії та вуглехімії ім. Л.М.Литвиненка НАН України, Донецький національний університет — Донецьк: «Вебер», 2008. — 758 с. — ISBN 978-966-335-206-0
• Лихтенберг А., Либерман М. Регулярная и стохастическая динамика. — М. : Мир, 1984. — 528 с.
• Шустер Г. Детерминированный хаос. Введение. — М. : Мир, 1988. — 248 с.
• Ott E. Chaos in Dynamical Systems. — Cambridge University Press, 2002. — ISBN 0-521-01084-5.