Плоскопаралельний рух
Плоскопарале́льний рух (пло́ский рух) твердого тіла — механічний рух твердого тіла, при якому всі його точки переміщаються паралельно до деякої нерухомої площини.
Плоский рух твердого тіла поширений в техніці, оскільки окремі ланки значної кількості механізмів і машин здійснюють тільки плоский рух (наприклад: рух колеса на прямолінійній ділянці шляху, робота корбово-гонкового, кулісного чи епіциклічного механізмів).
Рівняння плоскопаралельного руху[ред. | ред. код]


Із визначення плоскопаралельного руху випливає, що він повністю характеризується рухом плоскої фігури, утвореної перерізом тіла площиною, паралельною певній нерухомій площині. На основі цього можна вважати, що рух плоскої фігури відбувається в площині рисунка і, відповідно, рисунок є натуральним зображенням фігури. В свою чергу, положення плоскої фігури в координатній площині, наприклад, xOy, яка обрана за базову, визначається положенням будь-якого відрізка AB цієї фігури. З аналітичної геометрії відомо, що положення відрізка в площині його руху можна однозначно визначити координатами довільної точки відрізка (наприклад, координатами xA, yA точки A) і кутом φ між відрізком і однією з координатних осей (наприклад, віссю Ox). Точку, обрану для визначення положення плоскої фігури, називають полюсом.
Таким чином, закон руху плоскої фігури в її площині, а отже, і плоскопаралельного руху тіла в цілому, відносно обраної системи координат xOy описується трьома рівняннями:
Отже, вивчення плоского руху абсолютно твердого тіла можна звести до вивчення руху однієї плоскої фігури (перерізу), який визначається рухом трьох його точок, що не лежать на одній прямій. З аналізу залежностей випливає, що плоскопаралельний рух твердого тіла складається з поступального, при якому всі точки тіла рухаються як полюс, та обертального руху навколо полюса. Обертальна частина руху не залежить від обрання полюса, а поступальна залежить.
Основними кінематичними характеристиками плоскопаралельного руху є швидкість і прискорення полюса (в нашому випадку VA, aA), а також кутова швидкість ω і кутове прискорення ε тіла.
Визначення швидкостей точок тіла при плоскопаралельному русі[ред. | ред. код]
Оскільки плоский рух можна розглядати як такий, що складається з поступального і обертального рухів, то справедливим буде таке твердження: швидкість будь-якої точки твердого тіла, що здійснює плоскопаралельний рух, дорівнює геометричній (векторній) сумі швидкості полюса і лінійної швидкості цієї точки в її обертанні навколо полюса.
Для визначення швидкості будь-якої точки плоскої фігури розглянемо рух її довільної точки B, для якої можна записати:
При цьому швидкість визначається за числовим значенням і напрямом так само, як у випадку обертання, тобто і
Теорема про проєкції швидкостей двох точок[ред. | ред. код]
Із записаних вище залежностей можна отримати інші зручніші і простіші співвідношення, одне з яких дає така теорема: проєкції швидкостей двох точок твердого тіла на пряму, що проходить через ці точки, рівні між собою.
Миттєвий центр швидкостей[ред. | ред. код]
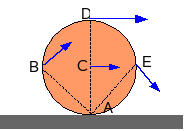
Можна довести, що при непоступальному русі плоскої фігури в кожний момент часу існує, і при тому єдина, точка з нульовою швидкістю.
Точка плоскої фігури, швидкість якої в даний момент часу дорівнює нулю, називається миттєвим центром швидкостей (МЦШ). Зазвичай точка розташування МЦШ позначається літерою P.
Якщо за полюс обрати МЦШ, тоді рівняння можна записати так
але за означенням і тому
Отже, якщо за полюс вибрати МЦШ, то плоскопаралельний рух тіла зводиться до миттєвого обертального руху навколо миттєвої осі, що проходить через МЦШ перпендикулярно до площини руху цього тіла. Модулі швидкостей всіх точок плоскої фігури будуть прямо пропорційними їх відстаням до МЦШ, а напрями векторів швидкостей будуть перпендикулярними до прямих, які з'єднують ці точки з МЦШ. Саме тому МЦШ називають також миттєвим центром обертання.
Див. також[ред. | ред. код]
Джерела[ред. | ред. код]
- Павловський М. А. Теоретична механіка: Підручник для студентів вищих навчальних закладів. — К.: Техніка, 2002. — 512 с. ISBN 966-575-184-0.
- Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1986. — 416 с.
Посилання[ред. | ред. код]
- Рейтій О. К. Теоретичнамеханіка (методичний посібник з лабораторних робіт). Частина І. Кінематика. — Ужгород: Видавництво УжНУ «Говерла», 2006. — 64 с.
|







