Власне прискорення

Діаграми в системах відліку спокою та мандрівника для власного прискорення 1g від стану спокою протягом одного року.

Простір-час мандрівника для постійного прискорення.

Власне прискорення в теорії відносності — фізичне прискорення (тобто прискорення, що вимірюється, наприклад допомогою акселерометра), якого зазнає об'єкт. Отже, це прискорення відносно вільного падіння або інерційного спостерігача, який на мить перебуває у стані спокою відносно вимірюваного об'єкта. Гравітація не викликає власного прискорення, оскільки гравітація впливає на інерційного спостерігача так, що власне прискорення не фіксується. Наслідком є те, що всі інерційні спостерігачі мають нульове власне прискорення.

Власне прискорення контрастує з координатним прискоренням, яке залежить від вибору системи координат і, отже, від вибору спостерігача.

У стандартних інерційних координатах спеціальної теорії відносності для однонапрямленого руху власним прискоренням є швидкість зміни власної швидкості відносно координатного часу.

В інерційній системі, в якій об'єкт миттєво перебуває у стані спокою, власний 3-вектор прискорення, об'єднаний з нульовою часовою компонентою, дає 4-прискорення об'єкта, що робить величину власного прискорення лоренц-інваріантною. Отже, концепція корисна в таких випадках: (i) з прискореними системами координат, (ii) на релятивістських швидкостях та (iii) у викривленому просторі-часі.

У прискорюваній ракеті після запуску або навіть у ракеті, що стоїть на старті, власне прискорення — це прискорення, яке відчувають пасажири, описуване як перевантаження (яке не є силою, а є саме прискоренням, див. докладніше у відповідній статті), створене самим транспортним засобом. «Прискорення гравітації» (пов'язане зі «силою тяжіння») ніколи не робить внеску у власне прискорення, а отже, власне прискорення, яке фіксують спостерігачі, що стоять на землі, обумовлене механічною силою із землі, а не «силою» чи « прискоренням» сили тяжіння. Якщо прибрати землю і дозволити спостерігачеві вільно падати, спостерігач зазнає координатного прискорення, але не матиме власного прискорення і, отже, не зазнає перевантаження. Зазвичай об'єкти в такому падінні або взагалі за будь-якого балістичного шляху (також званого інерційним рухом), зокрема, об'єкти на орбіті, не відчувають власного прискорення (нехтуючи невеликими припливними прискореннями для інерційних шляхів у гравітаційних полях). Цей стан також відомий як «невагомість» («нуль-g») або «вільне падіння».

Власне прискорення зводиться до координатного в інерційній системі координат у плоскому просторі-часі (тобто за відсутності сили тяжіння), за умови, що величина власної швидкості об'єкта (імпульс на одиницю маси) набагато менша за швидкість світла c. Тільки в таких ситуаціях координатне прискорення повністю відчувається як перевантаження (тобто власне прискорення, яке також визначають як таке, що створює вимірну вагу).

У ситуаціях, коли гравітація відсутня, але вибрана система координат не є інерційною, а прискорюється зі спостерігачем (наприклад, система відліку, пов'язана з ракетою, що прискорюється, або з об'єктами в центрифузі), то перевантаження та відповідне власне прискорення, яке фіксує спостерігач у подібній системі координат, викликані механічною силою протидії його вазі в цій системі. Цю вагу, у свою чергу, створюють сили інерції, які з'являються у всіх таких прискорених системах координат, подібно до ваги, створюваної «силою гравітації» для об'єктів, зафіксованих у просторі відносно гравітувального тіла (як на поверхні Землі).

Сумарну (механічну) силу, розраховану так, щоб викликати власне прискорення маси, яка перебуває в спокої в системі координат, яка має власне прискорення, за законом Ньютона F = m a називають власною силою. Як показано вище, власна сила дорівнює силі протидії, яка вимірюється як «робоча вага» об'єкта (тобто його вага, виміряна пристроєм, подібним до пружинної ваги, у вакуумі, в системі координат об'єкта). Таким чином, власна сила об'єкта завжди чисельно дорівнює та протилежна за напрямом виміряній вазі.

Приклади

Утримуючись на каруселі, яка обертається з постійною кутовою швидкістю, ви відчуваєте радіальне внутрішнє (доцентрове) власне прискорення через взаємодію між рукояткою і рукою. Це скасовує радіально зовнішнє геометричне прискорення, пов'язане з обертовою системою відліку. Це зовнішнє прискорення (з точки зору системи відліку, що обертається) стане координатним прискоренням, коли ви відпустите руки, що призведе до польоту геодезичною з нульовим власним прискоренням. Зрозуміло, в цей момент неприскорені спостерігачі у своїй системі відліку просто бачать, як зникають ваші рівні власне й координатне прискорення.

Анімація: відпускання рук на каруселі

Вигляд із нерухомої (ліворуч) і обертової (праворуч) систем відліку власного (червоне) і геометричного (синє) прискорень для об'єкта, випущеного з каруселі. З точки зору нерухомої системи відліку, небезпечна тангенціальна швидкість. З точки зору обертової системи відліку, небезпека може походити від геометричного прискорення. Примітка: У деяких вебоглядачах можна натиснути [Esc], щоб зупинити рух для детальнішого вивчення. Однак, для повторного старту анімації може знадобитися перезавантажити сторінку.

Так само, стоячи на планеті, що не обертається (і на землі), ми зазнаємо власного прискорення вгору завдяки нормальній (перпендикулярній до поверхні) силі, з якою земля діє на підошви нашого взуття. Вона нейтралізує геометричне прискорення у напрямку вниз через вибір системи координат (так звана система відліку поверхні (англ. shell frame)). Це прискорення вниз стає координатним, якщо ми випадково зробимо крок з обриву в траєкторію нульового власного прискорення (геодезична або система відліку дощу).

Анімація: м'яч скочується зі скелі

Зображення в системі відліку дощу (rain frame) і поверхні (shell frame) власного (червоне) і геометричного (синє) прискорення для об'єкта, що скочується зі скелі. Примітка: Система відліку дощу, на відміну краплі дощу, більш схожа на стрибок на батуті, траєкторія якого закінчується відразу, як м'яч досягає краю скелі. Система відліку поверхні знайома жителям планети, які покладаються на фізичне прискорення вгору від свого середовища, яке захищає їх від геометричного прискорення викривленого простору-часу. Не дивно, що спочатку мікрогравітаційне середовище може їх налякати.

Зверніть увагу, що геометричне прискорення (через член афінної зв'язності в системі координат коваріантної похідної) діє на кожен грам нашого тіла, тоді як власні прискорення зазвичай викликані зовнішньою силою. Вступні курси фізики часто розглядають гравітаційне прискорення вниз (геометричне) як наслідок гравітаційної сили. Це, поряд зі старанним ухиленням від неприскорених систем відліку, дозволяє їм розглядати координатне та власне прискорення як одну й ту саму сутність.

Навіть тоді, коли об'єкт у плоскому просторі-часі підтримує постійне власне прискорення протягом тривалого часу, нерухомі спостерігачі бачитимуть, що координатне прискорення об'єкта зменшується, у міру того як його координатна швидкість наближається до швидкості світла. Проте темп зростання власної швидкості об'єкта залишається постійним.

Анімація: швидке підняття і спуск

Вигляд у системі відліку спокою власного (червоне) та координатного (зелене) прискорень/сповільнень у вертикальному напрямку. Тут наш об'єкт спочатку прискорюється вгору протягом періоду часу 2*c/α за годинником мандрівника, де c — швидкість світла, а α — (червоне) величина власного прискорення. Цей перший етап триває близько 2 років, якщо величина прискорення становить близько 1g. Потім він прискорюється вниз (спочатку сповільнюється, а потім прискорюється) протягом подвоєного періоду, а потім уповільнюється 2*c/α, щоб повернутися на початкову висоту. Зверніть увагу, що координатне прискорення (зелене) помітне лише під час низькошвидкісних відрізків цієї подорожі.

Таким чином, відмінність між власним та координатним прискоренням дозволяє відстежувати досвід прискорених мандрівників з різних неньютонівських перспектив. Ці перспективи включають такі випадки як прискорені системи координат (наприклад, каруселі), високі швидкості (коли власні та координатні часи відрізняються) і викривлений простір-час (наприклад, пов'язаний із гравітацією на Землі).

Класичні застосування

На низьких швидкостях в інерційних системах координат ньютонівської фізики власне прискорення дорівнює координатному прискоренню a = d²x/dt². Однак, як сказано вище, воно відрізняється від координатного прискорення, якщо ви вибираєте (всупереч пораді Ньютона) опис світу з точки зору прискореної системи координат, наприклад, прискореного автомобіля або каменя, що обертається в пращі. Якщо ви погодитеся, що гравітація викликана кривиною простору-часу (див. нижче), у гравітаційному полі власне прискорення відрізняється від координатного.

Наприклад, об'єкт, що зазнав фізичного або власного прискорення a_o, спостерігач у системі координат, що має постійне прискорення a_frame, з координатним прискоренням:

${\vec {a}}_{acc}={\vec {a}}_{o}-{\vec {a}}_{frame}$.

Отже, якщо об'єкт прискорюється зі системою відліку, спостерігачі, закріплені в цій системі відліку, не бачитимуть ніякого прискорення.

Анімація: поїздка від блока до блока
Вигляд із нерухомої (map frame) та автомобільної (car frame) систем відліку фізичних (червоні) та геометричних (сині) прискорень для автомобіля, який рухається від одного знака зупинки до іншого. На цій ілюстрації автомобіль розганяється після знака зупинки до середини блока, після чого водій одразу відпускає газ і натискає на гальмо, щоб зробити наступну зупинку.

Аналогічно в об'єкта, який зазнає фізичного або власного прискорення a_o, спостерігач у системі, що обертається з кутовою швидкістю ω, виявить координатне прискорення:

${\vec {a}}_{rot}={\vec {a}}_{o}-{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})-2{\vec {\omega }}\times {\vec {v}}_{rot}-{\frac {d{\vec {\omega }}}{dt}}\times {\vec {r}}$.

У правій частині цього рівняння є три геометричні складові прискорення. Перша — «відцентрове прискорення», яке залежить тільки від радіального положення «r», а не від швидкості об'єкта, друга — «прискорення Коріоліса», яке залежить тільки від швидкості об'єкта в обертовій системі відліку v_rot, але не від його положення, а третя — «прискорення Ейлера», залежить тільки від положення та швидкості зміни кутової швидкості системи відліку.

Ньютонівський приклад: праща з постійною швидкістю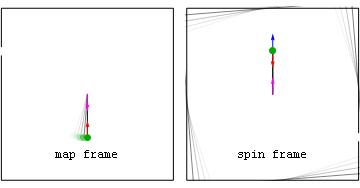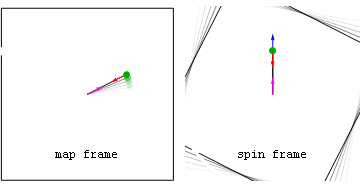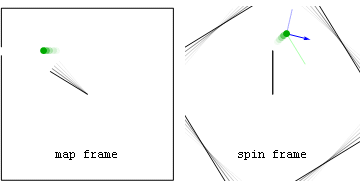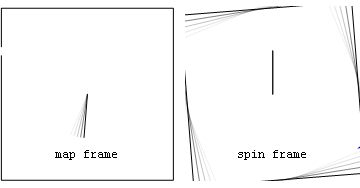

Прискорення та сили в нерухомій (map frame) і рухомій (spin frame) системах відліку, пов'язані з каменем, випущеним після того, як його розкрутили на невагомій мотузці. Сили на камені включають внутрішню доцентрову (червону) силу, що спостерігається в обох системах відліку, а також геометричну (синю) силу, що спостерігається в обертовій системі відліку. Перед тим, як камінь відпускають, синя геометрична сила є чисто відцентровою (спрямованою радіально назовні), а після відпускання геометрична сила є сумою відцентрового і коріолісового компонентів. Зверніть увагу, що після відпускання, в обертовій системі відліку відцентрова компонента (блакитна) завжди радіальна, а компонента Коріоліса (зелена) завжди перпендикулярна до швидкості обертової системи відліку. Також видно, що в обох системах сила «в точці кріплення мотузки» (пурпурна), викликана третім законом Ньютона, протидіє доцентровій силі на камені. Перед запуском каменя Такі альтернативні аналізи руху до відпускання каменя розглядають лише сили, які діють у радіальному напрямі. Обидва аналізи передбачають натяг мотузки T=mv2/r. Наприклад, якщо радіус лямки дорівнює r=1 м, швидкість каменю в нерухомій системі відліку дорівнює v=25 м/с, а маса каменя m=0,2 кг, то натяг мотузки становитиме 125 Н. Події в нерухомій системі координат перед запуском $-T_{centripetal}=\Sigma F_{radial}=ma_{radial}=-m{\frac {v^{2}}{r}}.$ Тут видно, що камінь весь час має прискорення усередину, щоб переміщатися круговою траєкторією радіуса r. Радіальне прискорення у радіальному напрямку aradial=v2/r викликає одна «незбалансована» доцентрова сила T. Той факт, що сила розтягу незбалансована, означає, що в цій системі відліку відцентрова (радіально-зовнішня) сила на камені дорівнює нулю. Події в обертовій системі відліку перед запуском $m{\frac {v^{2}}{r}}-T_{centripetal}=\Sigma F_{rot}=ma_{rot}=0.$ З точки зору обертової системи, можна сказати, що камінь зазнає дії збалансованої внутрішньої доцентрової (T) і відцентрової (mv2/r) сил, що приводить до відсутності будь-яких прискорень з точки зору цієї системи відліку. На відміну від доцентрової сили, яка залежить від системи відліку, відцентрова сила впливає на кожен шматочок каменя, що обертається, так само як гравітація діє на кожен наш грам. Крім того, величина відцентрової сили пропорційна масі каменя, тому прискорення буде незалежним від маси. Після запуску каменя Після того, як камінь вивільняється, в обертовій системі як доцентрові, так і коріолісові сили діють нелокалізовано на всі частини каменя з прискореннями, які не залежать від маси каменя. Для порівняння, в системі після вивільнення взагалі ніякі сили на камінь не діють.

У кожному з цих випадків фізичне або власне прискорення відрізняється від координатного прискорення, оскільки на останнє може впливати вибір системи координат, а також фізичні сили, що діють на об'єкт. Ті компоненти координатного прискорення, які не викликані фізичними силами (наприклад, прямим контактом або електростатичним тяжінням), часто приписують (як у наведеному вище прикладі Ньютона) силам, які: (i) діють на кожен грам об'єкта; (ii) викликають масово-незалежні прискорення та (iii) не існують з усіх точок зору. Такі геометричні (або невласні) сили включають сили Коріоліса, сили Ейлера, перевантаження, відцентрові сили і (як побачимо нижче) силу тяжіння.

Розгляд у плоскому просторі-часі

Відношення власного прискорення до координатного в 1+1-вимірному зрізі плоского простору-часу випливає з рівняння метрики плоского простору-часу Мінковського(cdτ)² = (cdt)² — (dx)². Тут єдина система відліку з лінійок та синхронізованих годинників визначає координатне положення x та координатний час t відповідно, годинник об'єкта, що рухається, визначає власний час τ, а «d» перед координатою означає нескінченно малу зміну. Ці співвідношення дозволяють вирішувати різні задачі «інжинірингу будь-яких швидкостей», хоча й лише з погляду розширеної системи відліку спостерігача, в якій визначається одночасність.

Прискорення (1+1)D

Цей графік показує, як космічний корабель із прискоренням 1 g (10 м/с² або близько 1,0 світлового року на рік у квадраті) протягом 100 років власного часу може долетіти до майже будь-якої частини спостережуваного Всесвіту і назад

В однонапрямленому випадку, коли прискорення об'єкта паралельне або антипаралельне його швидкості в 1+1-вимірному зрізі плоского простору-часу спостерігача, власне прискорення α та координатне прискорення a пов'язані через лоренц-фактор γ: α = γ³a. Отже, зміна власної швидкості w = dx/dτ є інтегралом від власного прискорення за координатним часом нерухомої системи відліку t, тобто Δw = αΔt для постійного α. На низьких швидкостях це зводиться до добре відомого рівняння, яке пов'язує координатну швидкість та координатне прискорення, помножене на координатний час, тобто Δv = aΔt.

За довільних швидкостей для постійного власного однонапрямленого прискорення існують аналогічні співвідношення між стрімкістю η і минулим власним часом Δτ, а також між лоренц-фактором γ та пройденою відстанню Δx, а саме:

$\alpha ={\frac {\Delta w}{\Delta t}}=c{\frac {\Delta \eta }{\Delta \tau }}=c^{2}{\frac {\Delta \gamma }{\Delta x}},$

де різні параметри швидкості пов'язані співвідношенням

$\eta =\operatorname {Arsh} \left({\frac {w}{c}}\right)=\operatorname {Arth} \left({\frac {v}{c}}\right)=\pm \operatorname {Arch} \gamma .$

Ці рівняння описують деякі наслідки прискореного руху із великою швидкістю. Наприклад, розглянемо космічний корабель, який може рухатися так, що його пасажири відчувають прискорення 1 g (10 м/с² або близько 1,0 світлового року на рік у квадраті); він проходить пів шляху до місця призначення, прискорюючись, а наступні пів шляху гальмує з тим самим прискоренням, щоб забезпечити для пасажирів земну штучну гравітацію на всьому шляху від точки A до точки B. Для відстані в системі спокою Δx_AB перше рівняння з наведених вище дає лоренц-фактор на середині шляху (тобто найбільше значення лоренц-фактору) γ_макс = 1 + α(Δx_AB/2)/c². Отже, час подорожі туди й назад за годинником корабля буде Δτ = 4(c/α) Arch γ_макс, а час подорожі, виміряний годинником у системі спокою, буде Δt = 4(c/α) sh (Arch γ_макс).

Цей уявний космічний корабель міг би здійснити подорож туди й назад від Землі до Проксими Центавра приблизно за 7,1 року за годинником мандрівників (близько 12 років за земним годинником), до чорної діри в центрі нашої Галактики (Стрілець A*) приблизно за 40 років (близько 54 тис. років за земним годинником), у Галактику Андромеди приблизно за 57 років (понад 5 мільйонів років за земним годинником). На практиці прискорення 1 g протягом багатьох років недосяжне, про що свідчить малюнок праворуч, який показує відношення найбільшого корисного навантаження до стартової маси.

Анімація: подорож до зорі на відстань 6,9 світлового року та назад.

Вигляд із системи спокою (ліворуч) і системи мандрівника (праворуч) подорожі в обидва боки з постійним прискоренням 1 g (червона стрілка в системі мандрівника) між Сонцем (жовтий кружечок) та гіпотетичною зорею (блакитний кружечок) на відстані 6,9 світлового року. Проксиму Центавра (помаранчевий кружечок) у 4 світлових роках від Сонця показано в лівому верхньому кутку З кожної точки зору рік минає за дві секунди анімації (100/17,4 кадру). Після кожного циклу пілоти на цьому човниковому рейсі старіють у два рази менше, ніж їхні колеги, що залишилися на Землі. Це прояв уповільнення часу. Інші відмінності включають змінення відстані між рухомими зорями, які видно в (прискореній) системі відліку мандрівників. Це прояв лоренцевого укорочення. Координатне прискорення (зелена стрілка), що спостерігається в системі відліку Землі, є значним лише протягом року після кожного запуску та за рік до прибуття (оскільки в середині шляху швидкість близька до швидкості світла і мало змінюється). При цьому власне прискорення (червона стрілка), яке відчувають мандрівники, значне і стале за модулем протягом усього рейсу. Також показано трасування світлового сигналу, ініційованого з кожної точки запуску, але через 0,886 року (в системі відліку Землі) після запуску. Цей імпульс досягає мандрівників у середній точці шляху, щоб нагадати їм про початок гальмування. У системі відліку Землі Проксима Центавра бачить відправлений із Землі імпульс (жовте коло) до того, як його побачить зоря призначення, але в системі мандрівника правильне протилежне: імпульс спочатку досягає зорі призначення, а потім — Проксими. Це прояв відносності одночасності. Проте обидва спостерігачі сходяться на думці про послідовність подій на будь-якій часоподібній світовій лінії.

У викривленому просторі-часі

Мовою загальної теорії відносності компоненти чотиривектора прискорення об'єкта A (величина якого є власним прискоренням) пов'язані з елементами чотиришвидкості через коваріантну похідну D за власним часом τ:

$$A^{\lambda }:={\frac {DU^{\lambda }}{d\tau }}={\frac {dU^{\lambda }}{d\tau }}+\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }$$

, де U — чотиришвидкість об'єкта, а Γ — 64 коефіцієнти зв'язку системи координат або символи Крістофеля. Зауважте, що грецькі індекси набувають чотирьох можливих значень, а саме 0 для осі часу та 1–3 для осей просторових координат, і що повторювані індекси використовуються для позначення підсумовування всіх значень цього індексу. Траєкторії з нульовим власним прискоренням називають геодезичними.

Ліва частина цього набору з чотирьох рівнянь (по одному для часоподібного і трьох простороподібних значень індексу λ) є 3-вектором власного прискорення об'єкта в поєднанні з нульовим часовим компонентом, як це видно з точки зору супутньої системи координат, у якій об'єкт перебуває в стані спокою. Перший член у правій частині вказує на яку величину змінюються часоподібні (енергія/mc) і простороподібні (імпульс/m) компоненти 4-швидкості U об'єкта за одиницю часу τ на рухомих годинниках.

Виразимо перший член у правій частині, оскільки на низьких швидкостях його просторові компоненти представляють координатне прискорення. Загалом, коли цей перший член дорівнює нулю, координатне прискорення об'єкта дорівнює нулю. Це дає

$${\frac {dU^{\lambda }}{d\tau }}=A^{\lambda }-\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }.$$

Отже, як показано на перших двох анімаціях вище, координатне прискорення стає нульовим щоразу, коли власне прискорення точно скасовується членом з'єднання (або геометричним прискоренням) праворуч. Застереження: цей член може бути сумою до шістнадцяти окремих членів, що залежать від швидкості та положення, оскільки повторювані індекси μ та ν за домовленістю підсумовуються за всіма парами їхніх чотирьох дозволених значень.

Сила і еквівалентність

Наведене вище рівняння також пропонує деяку точку зору на сили та принцип еквівалентності. Розглянемо локальну власну систему координат для метрики (наприклад, локальну тетраду Лоренца, подібну до тієї, про яку надають інформацію глобальні системи позиціонування), щоб описати час у секундах і простір в одиницях відстані вздовж перпендикулярних осей. Якщо ми помножимо наведене вище рівняння на масу спокою m рухомого об'єкта та поділимо на коефіцієнт Лоренца γ = dt/dτ, простороподібні компоненти виразять швидкість зміни імпульсу цього об'єкта в координатах, використаних для опису метрики.

Це, у свою чергу, можна розбити на частини завдяки власним і геометричним компонентам прискорення та сили. Якщо ми далі помножимо часоподібну складову на швидкість світла c і визначимо координатну швидкість як v = dx/dt, ми також отримаємо вираз для швидкості зміни енергії:

${\frac {dE}{dt}}={\vec {v}}\cdot {\frac {d{\vec {p}}}{dt}}$ (часоподібний) і ${\frac {d{\vec {p}}}{dt}}=\sum {\vec {f_{o}}}+\sum {\vec {f_{g}}}=m({\vec {a_{o}}}+{\vec {a_{g}}})$ (космічний).

Тут a_o — прискорення за рахунок власних сил, а_g — за замовчуванням, геометричне прискорення, яке з'являється в об'єкта через наш вибір системи координат. На низьких швидкостях ці прискорення поєднуються і створюють координатне прискорення, таке як a = d²x/dt², тоді як для однонапрямленого руху за будь-якої швидкості величина a_o є величиною власного прискорення α, як у розділі вище, де α = γ³a, коли a_g =0. Загалом виразити ці прискорення та сили може бути складно.

Тим не менш, якщо ми використовуємо цю розбивку для опису коефіцієнта зв'язку (Γ) вище в термінах геометричних сил, то рух об'єктів з точки зору будь-якої системи координат (принаймні на низьких швидкостях) можна розглядати як локально ньютонівський. Це вже звичайна практика, наприклад, із відцентровою силою та гравітацією. Таким чином, принцип еквівалентності поширює локальну корисність законів Ньютона на прискорені системи координат і за їх межі.

Мешканці поверхні планети

Для низькошвидкісних спостерігачів, які перебувають на фіксованій відстані від центра сферичної планети або зорі, координатне прискорення a_об (оболонки) приблизно пов'язане зі власним прискоренням a_o:

$${\vec {a}}_{\text{об}}={\vec {a}}_{\text{o}}-{\sqrt {\frac {r}{r-r_{s}}}}{\frac {GM}{r^{2}}}{\hat {r}}$$

де r_s = 2GM / c² — радіус Шварцшильда планети чи зорі. Коли радіус оболонки, на якій перебуває спостерігач, наближається до радіуса Шварцшильда, власне прискорення a_o, необхідне для того, щоб утримати його від падіння, стає величезним.

З іншого боку, якщо r ≫ r_s, то, щоб запобігти прискоренню вниз, потрібна власна сила, спрямована вгору, рівна лише GMm/r². На поверхні Землі маємо:

$${\vec {a}}_{\text{об}}={\vec {a}}_{o}-g{\hat {r}}$$

де g — 9,8 м/с², напрямлене вниз прискорення сили тяжіння, і ${\hat {r}}$ — одиничний вектор у радіальному напрямку від центра гравітувального тіла. Отже, тут, щоб утримати від прискорення вниз, необхідна зовнішня власна сила mg.

Чотиривекторні відхилення

Рівняння простору-часу в цьому розділі дозволяють за один раз обчислити всі відхилення між власним і координатним прискоренням. Наприклад, розрахуємо символи Крістоффеля:

$$\left({\begin{array}{llll}\left\{\Gamma _{tt}^{t},\Gamma _{tr}^{t},\Gamma _{t\theta }^{t},\Gamma _{t\phi }^{t}\right\}&\left\{\Gamma _{rt}^{t},\Gamma _{rr}^{t},\Gamma _{r\theta }^{t},\Gamma _{r\phi }^{t}\right\}&\left\{\Gamma _{\theta t}^{t},\Gamma _{\theta r}^{t},\Gamma _{\theta \theta }^{t},\Gamma _{\theta \phi }^{t}\right\}&\left\{\Gamma _{\phi t}^{t},\Gamma _{\phi r}^{t},\Gamma _{\phi \theta }^{t},\Gamma _{\phi \phi }^{t}\right\}\\\left\{\Gamma _{tt}^{r},\Gamma _{tr}^{r},\Gamma _{t\theta }^{r},\Gamma _{t\phi }^{r}\right\}&\left\{\Gamma _{rt}^{r},\Gamma _{rr}^{r},\Gamma _{r\theta }^{r},\Gamma _{r\phi }^{r}\right\}&\left\{\Gamma _{\theta t}^{r},\Gamma _{\theta r}^{r},\Gamma _{\theta \theta }^{r},\Gamma _{\theta \phi }^{r}\right\}&\left\{\Gamma _{\phi t}^{r},\Gamma _{\phi r}^{r},\Gamma _{\phi \theta }^{r},\Gamma _{\phi \phi }^{r}\right\}\\\left\{\Gamma _{tt}^{\theta },\Gamma _{tr}^{\theta },\Gamma _{t\theta }^{\theta },\Gamma _{t\phi }^{\theta }\right\}&\left\{\Gamma _{rt}^{\theta },\Gamma _{rr}^{\theta },\Gamma _{r\theta }^{\theta },\Gamma _{r\phi }^{\theta }\right\}&\left\{\Gamma _{\theta t}^{\theta },\Gamma _{\theta r}^{\theta },\Gamma _{\theta \theta }^{\theta },\Gamma _{\theta \phi }^{\theta }\right\}&\left\{\Gamma _{\phi t}^{\theta },\Gamma _{\phi r}^{\theta },\Gamma _{\phi \theta }^{\theta },\Gamma _{\phi \phi }^{\theta }\right\}\\\left\{\Gamma _{tt}^{\phi },\Gamma _{tr}^{\phi },\Gamma _{t\theta }^{\phi },\Gamma _{t\phi }^{\phi }\right\}&\left\{\Gamma _{rt}^{\phi },\Gamma _{rr}^{\phi },\Gamma _{r\theta }^{\phi },\Gamma _{r\phi }^{\phi }\right\}&\left\{\Gamma _{\theta t}^{\phi },\Gamma _{\theta r}^{\phi },\Gamma _{\theta \theta }^{\phi },\Gamma _{\theta \phi }^{\phi }\right\}&\left\{\Gamma _{\phi t}^{\phi },\Gamma _{\phi r}^{\phi },\Gamma _{\phi \theta }^{\phi },\Gamma _{\phi \phi }^{\phi }\right\}\end{array}}\right)$$

для дальньої координатної метрики Шварцшильда (c dτ)² = (1−r_s/r)(c dt)² − (1/(1−r_s/r))dr² − r² dθ² − (r sin θ)² dφ², де r_s = 2GM / c² — радіус Шварцшильда. Отриманий масив коефіцієнтів має вигляд:

$$\left({\begin{array}{llll}\left\{0,{\frac {r_{s}}{2r(r-r_{s})}},0,0\right\}&\left\{{\frac {r_{s}}{2r(r-r_{s})}},0,0,0\right\}&\{0,0,0,0\}&\{0,0,0,0\}\\\left\{{\frac {r_{s}c^{2}(r-r_{s})}{2r^{3}}},0,0,0\right\}&\left\{0,{\frac {r_{s}}{2r(r_{s}-r)}},0,0\right\}&\{0,0,r_{s}-r,0\}&\left\{0,0,0,(r_{s}-r)\sin ^{2}\theta \right\}\\\{0,0,0,0\}&\left\{0,0,{\frac {1}{r}},0\right\}&\left\{0,{\frac {1}{r}},0,0\right\}&\{0,0,0,-\cos \theta \sin \theta \}\\\{0,0,0,0\}&\left\{0,0,0,{\frac {1}{r}}\right\}&\{0,0,0,\cot(\theta )\}&\left\{0,{\frac {1}{r}},\cot \theta ,0\right\}\end{array}}\right).$$

Із цього можна отримати власне прискорення системи відліку оболонки, прирівнявши координатне прискорення до нуля і, отже, вимагаючи, щоб власне прискорення скасувало геометричне прискорення нерухомого об'єкта, тобто $A^{\lambda }=\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }=\{0,GM/r^{2},0,0\}$. Це ще не розв'язує задачу, оскільки координати Шварцшильда у викривленому просторі-часі є супутніми координатами, а не координатами локального спостерігача. Однак, величина наведеного вище власного 4-вектора прискорення, а саме ${\textstyle \alpha ={\sqrt {1/(1-r_{s}/r)}}GM/r^{2}}$, це саме те, що нам потрібно, тобто напрямлене вгору незалежне від системи відліку власне прискорення, необхідне для протидії геометричному прискоренню вниз, якого зазнають мешканці поверхні планети.

Окремим випадком наведеного вище набору символів Крістоффеля є набір сферичних координат плоского простору, отриманий прирівнянням вище r_s або M до нуля:

$$\left({\begin{array}{llll}\left\{0,0,0,0\right\}&\left\{0,0,0,0\right\}&\{0,0,0,0\}&\{0,0,0,0\}\\\left\{0,0,0,0\right\}&\left\{0,0,0,0\right\}&\{0,0,-r,0\}&\left\{0,0,0,-r\sin ^{2}\theta \right\}\\\{0,0,0,0\}&\left\{0,0,{\frac {1}{r}},0\right\}&\left\{0,{\frac {1}{r}},0,0\right\}&\{0,0,0,-\cos \theta \sin \theta \}\\\{0,0,0,0\}&\left\{0,0,0,{\frac {1}{r}}\right\}&\{0,0,0,\cot \theta \}&\left\{0,{\frac {1}{r}},\cot \theta ,0\right\}\end{array}}\right).$$

З цього можна отримати, наприклад, власне доцентрове прискорення, необхідне для компенсації відцентрового геометричного прискорення об'єкта, що рухається зі сталою кутовою швидкістю ω = dφ/dτ на екваторі, де θ = π/2. Формування тієї ж 4-векторної суми, що й вище, для випадку нульових dθ/dτ і dr/dτ дає не що інше, як класичне прискорення для обертального руху, наведене вище, тобто $A^{\lambda }=\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }=\{0,-r(d\phi /d\tau )^{2},0,0\}$ так що a_o = ω²r. Ефекти Коріоліса також містяться в цих коефіцієнтах зв'язку і подібно виникають лише з геометрії системи координат.

Див. також

• 4-вектор
• Кінематика
• Прискорення
• Сила інерції

Посилання

• Уривки з першого видання Spacetime Physics та інші ресурси, опубліковані Едвіном Ф. Тейлором
• Сторінка книги про гравітацію Джеймса Гартла, включно з програмами Mathematica для обчислення символів Крістоффеля.
• Нотатки та програми Ендрю Гамільтона для роботи з локальними тетрадами в Університеті Колорадо, Боулдер.