Розподіл степенів

Наука про мережі
Теорія
Граф Складні мережі Світ тісний Безмасштабна мережа Перколяція Структура спільноти Еволюція Керованість Візуалізація графів Соціальний капітал Аналіз зв’язків Оптимізація Транзитивність Теорія балансу Ефект мережі Соціальний вплив
Види мереж
Інформаційна (комп'ютерна) Телекомунікаційна Транспортна Соціальна аналіз Біологічна Штучна нейронна мережа Семантична Просторова Залежностей Потокова
Графи
Властивості Кліка Компонент Розріз Цикл Структура даних Ребро Петля Окіл Шлях Вершина Список суміжності / матриця Список інцидентності / матриця Види Двочастковий Повний Орієнтований Гіперграф Мультиграф Випадковий Зважений
Метрики Алгоритми
Центральність Степінь Близькість PageRank Кластеризація Асортативність Відстань Модулярність Ефективність
Моделі
Топологія Випадковий граф Модель Ердеша — Реньї Модель Барабаші — Альберт Модель Воттса — Строгаца Гіперболічна (HGN) Ієрархічна Стохастична блокова модель Динаміка Булева мережа Агентне моделювання Епідемічні/SIR
Списки Категорії
Категорія:Теорія мереж Категорія:Теорія графів

При дослідженні графів та мереж, степінь вузла в мережі — це кількість зв'язків з іншими вузлами, а розподіл степенів — це розподіл ймовірностей цих степенів усією мережею.

Визначення

Степінь вузла в мережі (іноді неправильно вживається як зв'язність) — це кількість з'єднань з іншими вузлами або кількість ребер вузла. Якщо мережа орієнтована, це означає, що ребра вказують у напрямку з одного вузла до іншого. У такому випадку вузли мають два різних степені: вхідний степінь, що дорівнює кількості вхідних ребер, та вихідний степінь, що дорівнює кількості вихідних ребер.

Розподіл степенів P(k) мережі визначається як відношення кількості вузлів у мережі зі степенем k до кількості всіх вузлів у цій мережі. Таким чином, якщо мережа складається з n вузлів і n_k з них мають степінь k, то маємо $P(k)={\frac {n_{k}}{n}}$.

Ця інформація іноді представлена у вигляді кумулятивного розподілу степенів, частки вузлів зі степенем, меншим за k, або навіть додаткового кумулятивного розподілу степенів, частки вузлів зі степенем, який більший або дорівнює k, що позначається як (1 — C), якщо розглядати C, як сукупний розподіл степенів; тобто, доповнення до C.

Спостережувані розподіли степенів

Розподіл степенів є дуже важливим при вивченні як реальних мереж, таких як інтернет чи соціальні мережі, так і теоретичних мереж. Найпростіша модель мережі — випадковий граф (модель Ердеша — Реньї), в якому кожен з n вузлів може бути незалежно пов'язаним (чи ні) з ймовірністю p (або 1 − p), має біноміальний розподіл степенів k:

$P(k)={n-1 \choose k}p^{k}(1-p)^{n-1-k},$

(або розподіл Пуассона в межах великого n, якщо середній степінь $\langle k\rangle =p(n-1)$ є фіксованим). Однак більшість реальних мереж мають розподіл степенів, що дуже відрізняються від попереднього. Більшість із них мають значне відхилення праворуч, що позначає, що більша кількість вузлів мають низький степінь, та лише невелика кількість, відома як «хаби», мають високий степінь. Стверджувалося, що певні мережі, зокрема Інтернет, Всесвітня мережа та деякі соціальні мережі, мають розподіл степенів, які приблизно відповідають степеневому закону: $P(k)\sim k^{-\gamma }$, де γ — константа. Такі мережі називаються безмасштабними мережами та вони привертають особливу увагу своїми структурними та динамічними властивостями. Однак дослідження широкого кола реальних мереж показує, що безмасштабні мережі, якщо їх оцінювати за допомогою точних статистичних показників зустрічаються рідко. Деякі дослідники заперечують ці висновки, стверджуючи, що визначення, які було використано у дослідженні, є невідповідно жорсткими, у той час, як інші стверджують, що точна функціональна форма розподілу степенів менш важлива, ніж знання того, чи є розподіл степенів розподілом з товстим хвостом чи ні. Надмірну інтерпретацію конкретних форм розподілу степенів також критикували за те, що вона не враховувала, як мережі можуть розвиватися з часом.

Надмірний розподіл степенів

Надмірний розподіл степенів — це розподіл ймовірностей, для вузла, досягнутого за ребром, кількості інших ребер, які ведуть до цього вузла. Іншими словами, це розподіл вихідних зв'язків вузла, досягнутого за ребром.

Припустимо, що мережа має розподіл степенів $P(k)$, після вибору вузла (випадково чи ні) і переходу до одного з його сусідів (припускаючи, що він має принаймні одного сусіда), ймовірність того, що цей вузол матиме $k$ сусідів не визначається $P(k)$. Причиною цього є те, що кожен раз, коли якийсь вузол вибирається в гетерогенній мережі, більш ймовірно досягти хабу, дотримуючись одного з наявних сусідів цього вузла. Справжня ймовірність того, що такі вузли мають степінь $k$ є $q(k)$ яка називається надмірним степенем цього вузла. У моделі конфігурації, кореляції між вузлами, які проігноровані, і кожним вузлом, стосовно якого припускається, що його можна з'єднанати з будь-якими іншими вузлами мережі з однаковою імовірністю, надмірний розподіл степенів можна записати у такому вигляді:

$q(k)={\frac {k+1}{\langle k\rangle }}P(k+1),$

де ${\langle k\rangle }$ — середній степінь моделі. Звідси випливає, що середній степінь сусіда будь-якого вузла є більшим за середній степінь цього вузла. На прикладі соціальних мереж це буде означати, що, у середньому, у ваших друзів більше друзів, ніж у вас. Це відомо як парадокс дружби. Можна показати, що мережа може мати гігантську компоненту, якщо її середній надмірний степінь більший за одиницю: $\sum _{k}kq(k)>1\Rightarrow {\langle k^{2}\rangle }-2{\langle k\rangle }>0$

Майте на увазі, що останні два рівняння виконуються лише для моделі конфігурації, і щоб отримати надмірний розподіл степенів для реальних мереж, кореляція степенів повинна бути врахована.

Метод твірних функцій

Твірні функції можна використовувати для обчислення певних властивостей випадкових мереж. Використовуючи розподіл степенів та надмірний розподіл степенів певної мережі, $P(k)$ і $q(k)$ відповідно, можна записати два степеневих ряди в такому вигляді:

$G_{0}(x)=\textstyle \sum _{k}\displaystyle P(k)x^{k}$ і $G_{1}(x)=\textstyle \sum _{k}\displaystyle q(k)x^{k}=\textstyle \sum _{k}\displaystyle {\frac {k}{\langle k\rangle }}P(k)x^{k-1}$

$G_{1}(x)$ також можна отримати використовуючи похідну $G_{0}(x)$ :

$G_{1}(x)={\frac {G'_{0}(x)}{G'_{0}(1)}}$

Якщо твірна функція для розподілу ймовірностей $P(k)$ відома, то можливо відновити значення $P(k)$ шляхом диференціювання:

$P(k)={\frac {1}{k!}}{\operatorname {d} ^{k}\!G \over \operatorname {d} \!x^{k}}{\biggl \vert }_{x=0}$

Певні властивості, такі як моменти, можуть бути легко обчислені за допомогою ряду $G_{0}(x)$ та його похідних:

• ${\langle k\rangle }=G'_{0}(1)$
• ${\langle k^{2}\rangle }=G''_{0}(1)+G'_{0}(1)$

Та у загальному випадку:

• ${\langle k^{m}\rangle }={\Biggl [}{{\bigg (}\operatorname {x} {\operatorname {d} \! \over \operatorname {dx} \!}{\biggl )}^{m}}G_{0}(x){\Biggl ]}_{x=1}$

Для пуассонівських випадкових мереж, таких як графік ER, $G_{1}(x)=G_{0}(x)$, через це теорія випадкових мереж такого типу є доволі простою. Розподіли ймовірностей для перших найближчих сусідів породжується функцією $G_{0}(x)$ та для других функцією $G_{0}(G_{1}(x))$. У загальному випадку, розподіл для $m$-их найближчих сусідів генерується таким чином:

$G_{0}{\bigl (}G_{1}(...G_{1}(x)...){\bigr )}$, де функція $G_{1}$ діє сама на себе $m-1$ раз.

Середня кількість перших сусідів, $c_{1}$, є ${\langle k\rangle }={dG_{0}(x) \over dx}|_{x=1}$ а середня кількість других сусідів дорівнює: $c_{2}={\biggl [}{d \over dx}G_{0}{\big (}G_{1}(x){\big )}{\biggl ]}_{x=1}=G_{1}'(1)G'_{0}{\big (}G_{1}(1){\big )}=G_{1}'(1)G'_{0}(1)=G''_{0}(1)$

Розподіл степенів для орієнтованих мереж

Вхідний/вихідний розподіл степенів для графіка гіперпосилання Вікіпедії (логарифмічні шкали)

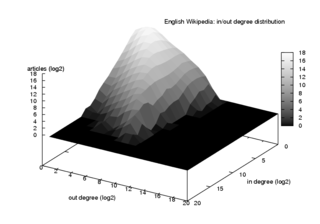
В орієнтованій мережі кожен вузол має певний вхідний степінь $k_{in}$ і певний вихідний степінь $k_{out}$, що дорівнюють кількості вхідних та вихідних ребер відповідно. Якщо $P(k_{in},k_{out})$ це ймовірність того, що випадково вибраний вузол має вхідний степінь $k_{in}$ і вихідний степінь $k_{out}$, тоді твірну функцію, призначену цьому спільному розподілу ймовірностей, можна записати з двома змінними $x$ і $y$ у вигляді: ${\mathcal {G}}(x,y)=\sum _{k_{in},k_{out}}\displaystyle P({k_{in},k_{out}})x^{k_{in}}y^{k_{out}}.$

Оскільки кожне ребро в орієнтованій мережі має виходити з одного вузла та входити в інший, то середня кількість ребер, що входять у вузол, дорівнює нулю. Тому

$\langle {k_{in}-k_{out}}\rangle =\sum _{k_{in},k_{out}}\displaystyle (k_{in}-k_{out})P({k_{in},k_{out}})=0$,

це означає, що твірна функція повинна задовольняти умові:

${\partial {\mathcal {G}} \over \partial x}\vert _{x,y=1}={\partial {\mathcal {G}} \over \partial y}\vert _{x,y=1}=c,$

де $c$ — середній степінь (як вхідний, так і вихідний) усіх вузлів у мережі; $\langle {k_{in}}\rangle =\langle {k_{out}}\rangle =c.$

Використовуючи функцію ${\mathcal {G}}(x,y)$, знов можна знайти твірну функцію для розподілу вхідного/вихідного степенів та надмірного розподілу вхідного/вихідного степенів, як і раніше. $G_{0}^{in}(x)$ можна визначити як твірну функцію кількості вхідних ребер для випадково вибраного вузла, та $G_{1}^{in}(x)$ можна визначити як кількість вхідних ребер до вузла, отриманого шляхом переходу за випадковим ребром. Також можна визначити твірні функції $G_{0}^{out}(y)$ і $G_{1}^{out}(y)$ для числа вихідних ребер з такого вузла:

• $G_{0}^{in}(x)={\mathcal {G}}(x,1)$
• $G_{1}^{in}(x)={\frac {1}{c}}{\partial {\mathcal {G}} \over \partial x}\vert _{y=1}$
• $G_{0}^{out}(y)={\mathcal {G}}(1,y)$
• $G_{1}^{out}(y)={\frac {1}{c}}{\partial {\mathcal {G}} \over \partial y}\vert _{x=1}$

Тут, середня кількість перших сусідів $c$, або як було введено раніше $c_{1}$, дорівнює ${\partial {\mathcal {G}} \over \partial x}{\biggl \vert }_{x,y=1}={\partial {\mathcal {G}} \over \partial y}{\biggl \vert }_{x,y=1}$ та середня кількість других сусідів, досяжних з випадково вибраного вузла, визначається так: $c_{2}=G_{1}'(1)G'_{0}(1)={\partial ^{2}{\mathcal {G}} \over \partial x\partial y}{\biggl \vert }_{x,y=1}$. Оскільки ці рівняння симетричні відносно $x$ та $y$, то вони визначають також значення для перших та других сусідів, з яких можна досягти випадкового вузла.

Розподіл степенів для мереж зі знаком

У знакових мережах кожен вузол має додатний степінь $k_{+}$ і від'ємний степінь $k_{-}$, які є відповідно додатною кількістю ребер і від'ємною кількістю ребер, з'єднаних з цим вузлом. Таким чином $P(k_{+})$ і $P(k_{-})$ позначають негативний розподіл степенів та позитивний розподіл степенів для мереж зі знаком.

Див. також

• Теорія графів
• Складна мережа
• Безмасштабна мережа
• Випадковий графік
• Структурне відсікання

Посилання

• Albert, R.; Barabasi, A.-L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics. 74 (1): 47—97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47.
• Dorogovtsev, S.; Mendes, J. F. F. (2002). Evolution of networks. Advances in Physics. 51 (4): 1079—1187. arXiv:cond-mat/0106144. Bibcode:2002AdPhy..51.1079D. doi:10.1080/00018730110112519.
• Newman, M. E. J. (2003). The structure and function of complex networks. SIAM Review. 45 (2): 167—256. arXiv:cond-mat/0303516. Bibcode:2003SIAMR..45..167N. doi:10.1137/S003614450342480.