Біноміальний розподіл

Біноміальний розподіл

Функція ймовірностей
Функція розподілу ймовірностей 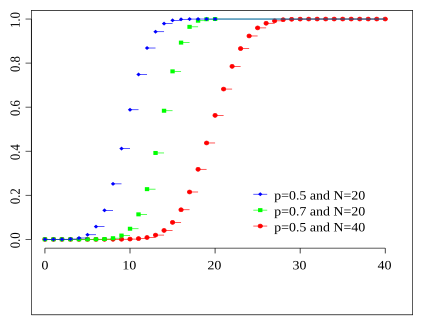Кольори збігаються з попереднім малюнком
Параметри	$n \geq 0$ кількість випробувань (ціле) $0\leq p \leq 1$ ймовірність успіху (дійсне)
Носій функції	$k \in \{0,\dots,n\}\!$
Розподіл ймовірностей	${n\choose k} p^k (1-p)^{n-k} \!$
Функція розподілу ймовірностей (cdf)	$I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!$
Середнє	$np\!$
Медіана	одне із $\{\lfloor np\rfloor, \lceil np \rceil\}$
Мода	$\lfloor (n+1)\,p\rfloor\!$
Дисперсія	$np(1-p)\!$
Коефіцієнт асиметрії	$\frac{1-2p}{\sqrt{np(1-p)}}\!$
Коефіцієнт ексцесу	$\frac{1-6p(1-p)}{np(1-p)}\!$
Ентропія	$\frac{1}{2} \ln \left( 2 \pi n e p (1-p) \right) + O \left( \frac{1}{n} \right)$
Твірна функція моментів (mgf)	$(1-p + pe^t)^n \!$
Характеристична функція	$(1-p + pe^{it})^n \!$

Дискретна випадкова величина ξ називається такою, що має біноміальний розподіл, якщо ймовірність набуття нею конкретних значень має вигляд: $P(\xi=k) = C_n^k p^k q^{n-k}, k = 0,1,...n$, де p, n — параметри, що визначають розподіл, $p\in[0,1], q=1-p, n\in\mathbb{N}$.

Позначається $\mathcal{L}(\xi)=Bi(n,p)$.

Пояснення

В теорії ймовірностей та математичній статистиці, біноміальний розподіл є дискретним ймовірносним розподілом, що характеризує кількість успіхів в послідовності експериментів, значення яких змінюється за принципом так/ні, кожен з яких набуває успіху з ймовірністю p. Такі так/ні експерименти також називаються експериментами Бернулі, або схемою Бернуллі, зокрема, якщо n=1 (кількість випробувань), то отримаємо Розподіл Бернуллі.

Числові характеристики

Зважаючи на співвідношення між біноміальним розподілом і розподілом Бернуллі, неведені нижче, а також на властивості математичного сподівання і дисперсії, можна отримати числові характеристики для біноміального розподілу без громіздких обчислень.

Математичне сподівання

$M\xi=M\sum_{i=1}^n\xi_i=\sum_{i=1}^n p=np$, де $\mathcal{L}(\xi_i)=B(p), i=\overline{1,n}$.

Дисперсія

$D\xi=D\sum_{i=1}^n\xi_i=\sum_{i=1}^n pq=npq$, де $\mathcal{L}(\xi_i)=B(p), i=\overline{1,n}$.

Зв'язок з іншими розподілами

• Нехай незалежні випадкові величини $\xi_1, \xi_2, ... , \xi_n$ мають розподіл Бернуллі з параметром p, тобто $\mathcal{L}(\xi_i)=B(p), i=\overline{1,n}$, тоді випадкова величина $\xi=\sum_{i=1}^n\xi_i$ має біноміальний розподіл з параметрами p, n, тобто $\mathcal{L}(\xi)=Bi(n,p)$.
• Якщо випадкова величина має біноміальний розподіл з першим параметром n=1, то вона є розподіленою за законом Бернуллі.

Див. також

• Розподіл Бернуллі
• Розподіл ймовірностей
• Схема Бернуллі
• Функція розподілу ймовірностей