Фільтр Ґабора

Лінійні електронні фільтри
Фільтр Баттерворта
Фільтр Чебишова
Еліптичний фільтр
Фільтр Бесселя
Фільтр Гауса
Фільтр Лежандра
Фільтр Габора

Приклад двохвимірного фільтра Ґабора

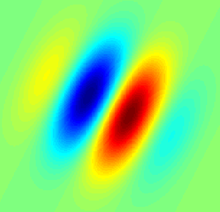
Фільтр Ґабора — лінійний електронний фільтр, імпульсна перехідна характеристика якого визначається у вигляді гармонійної функції, помноженої на функцію Гауса. Через властивість відповідності згортки в частотній області множенню у часовій області, перетворення Фур'є імпульсної передавальної характеристики фільтра Ґабора є згорткою перетворень Фур'є гармонійної функції і функції Гауса.

$g(x,y;\lambda ,\theta ,\psi ,\sigma ,\gamma )=\exp(-{\frac {x'^{2}+\gamma ^{2}y'^{2}}{2\sigma ^{2}}})\cos(2\pi {\frac {x'}{\lambda }}+\psi )$

де

$x'=x\cos \theta +y\sin \theta \,$

і

$y'=-x\sin \theta +y\cos \theta \,$

У цьому рівнянні $\lambda$ являє собою довжину хвилі множника-косинуса, $\theta$ визначає орієнтацію нормалі паралельних смуг функції Ґабора в градусах, $\psi$ — зсув фаз у градусах і $\gamma$ — коефіцієнт стиснення, що характеризує еліптичність функції Ґабора.

Приклад реалізації фільтру Габора для пакету Matlab:

function gb = gabor_fn(sigma_x, sigma_y, theta, lambda, psi, gamma)

sz_x = fix(6 * sigma_x);
if mod(sz_x,2)==0, sz_x = sz_x + 1; end
	

sz_y = fix(6 * sigma_y);
if mod(sz_y, 2)==0, sz_y = sz_y + 1; end

[x y] = meshgrid(-fix(sz_x/2):fix(sz_x/2), fix(-sz_y/2):fix(sz_y/2));

% Поворот
x_theta = x*cos(theta) + y*sin(theta);
y_theta = -x*sin(theta) + y*cos(theta);

gb = exp(-.5 * (x_theta^2/sigma_x^2 + gamma^2 * y_theta.^2/sigma_y^2))* cos(2 * pi/lambda * x_theta + psi);

Фільтри Ґабора безпосередньо пов'язані з вейвлетами Ґабора, оскільки вони можуть бути сконструйовані шляхом ряду стиснень і обертань. Простір Ґабора (згортка фільтра з сигналом) часто застосовується в різних додатках обробки зображень, зокрема, для розпізнавання райдужної оболонки в біометричних системах безпеки і в автоматизованих системах контролю доступу на підставі розпізнавання відбитків пальців.

Див. також

• Перетворення Ґабора
• Денніс Ґабор