Гальмівне випромінювання

Гальмівне випромінювання зарядженого електрона, що розсіюється на додатньо зарадженому йоні.

Перетин гальмівного випромінювання фотонів з енергією 30 кеВ при зіткненні електрона з протоном.

Гальмі́вне випромі́нювання (нім. Bremsstrahlung бремсштралунґ, англ. deceleration radiation) — електромагнітне випромінювання заряджених частинок при зіткненні з іншими зарядженими частинками, зазвичай електронами чи атомними ядрами.

Заряджена частинка, що рухається рівномірно, не випромінює електромагнітних хвиль. Створені нею електричне і магнітне поля залишаються близькими і не відриваються від частинки, утворюючи незалежну хвилю.

Випромінювання з'являється тоді, коли заряджена частинка рухається із прискоренням. Однією з причин прискореного руху може бути зіткнення з іншою частинкою, в результаті якого міняється траєкторія руху. Таке випромінювання називають гальмівним, бо воно забирає із собою частину енергії зарядженої частинки, додатково гальмуючи її. Зокрема гальмівне випромінювання виникає при зіткненні пучка електронів з речовиною електрода.

Гальмівним називають лише випромінювання, що утворюється через прискорення у електричному полі. Випромінювання, що виникає через прискорення в магнітному полі називається магнітногальмівним. Таким є синхротронне або циклотронне випромінювання.

Історія

Ймовірно, вперше гальмівне випромінювання спостерігав Нікола Тесла в кінці 19-го століття, проте його результати не набули широкого розголосу. У 1895 році, Вільгельм Рентген показав, що пучок електронів у вакуумній лампі породжує випромінювання (гамма-промені) при зіткненні з речовиною (наприклад, речовиною самої лампи) . У 1915 році Вільямом Дуейном і Франкліном Хантом було встановлено емпіричну залежність максимальної енергій фотонів від енергії падаючих електронів. У 1922 році Хельмутом Куленкампфом було відкрито, що спектр гальмівного випромінювання є суцільним, а також описана його форма. Перша (класична) теорія гальмівного випромінювання була розроблена Гендріком Крамерсом невдовзі після цього.

Теорія гальмівного випромінювання, що враховує квантовомеханічні ефекти, була розроблена Зоммерфельдом в 1929 році.

Теорії гальмівного випромінювання

Класична теорія

У класичній електродинаміці будь-який заряд, що прискорюється, буде створювати електромагнітні хвилі. Прискорення, що його створює ядро з зарядом Ze на частинку з зарядом ze і масою m, буде дорівнювати Zze²/m. Тоді інтенсивність випромінювання буде пропорційною Z²z²/m². Таким чином, з одного боку, інтенсивність випромінювання пропорційна квадрату атомного номера елемента, на якому гальмуються частинки. З іншого боку, інтенсивність випромінення сильно залежить від маси розсіюваної частинки. Через це, випромінювання, що створюють протони або альфа-частинки має інтенсивність в мільйони разів меншу, ніж електрони, при розсіянні на тій же речовині. Навіть найлегша частинка, важча за електрон, мюон — в 212 разів важча за нього, а отже, породжує випромінювання в 40 000 разів менш інтенсивне. Через це, на практиці, розглядається лише гальмівне випромінювання, що створюється електронами або позитронами.

Квантова електродинаміка

У квантовій теорії електрон у кулонівському полі має деяку ймовірність перейти у стан з нижчою енергією, випромінивши при цьому фотон (існує ймовірність утворення кількох фотонів у цьому процесі, проте вона вкрай мала). Цей процес, по суті, є непружним розсіянням електрона на ядрі. Можливе і пружне розсіяння, при якому енергія електрона не змінюється, і фотон не випромінюється, причому більшість розсіянь є саме такими (для низькоенергетичних електронів і легких ядер, лише 1/137 від усіх розсіянь є непружними).

Ця ймовірність, в загальному випадку, залежить від енергії самого електрона. У нерелятивістському наближенні, переріз випромінення електрона з енергією k, для електрона, що пролітає на відстані r₀ від ядра дорівнює:

$\phi _{k}d\left({\frac {k}{T_{0}}}\right)={\frac {Z^{2}r_{0}^{2}}{137}}{\frac {16}{3}}{\frac {dk}{k}}{\frac {\mu ^{2}}{p_{0}^{2}}}{\text{ln}}{\frac {p_{0}+p}{p_{0}-p}}$,

де Z — заряд ядра, μ — енергія спокою електрона, T⁰ — кінетична енергія електрона, p₀ та p — імпульс електрону до і після зіткнення.

Таким чином, в першому наближенні можна сказати, що ймовірність утворення фотона обернено пропорційна його енергії. З іншого боку, у крайньому випадку надвисоких енергій, розподіл має наступний вигляд:

$\phi _{k}d\left({\frac {k}{E_{0}}}\right)=2{\frac {Z^{2}r_{0}^{2}}{137}}{\frac {dk}{k}}{\frac {E}{E_{0}}}\left[{\frac {E_{0}^{2}+E^{2}}{E_{0}E}}-{\frac {2}{3}}\right]\left[2{\text{ln}}{\frac {2E_{0}E}{\mu k}}-1\right]$

Як можна бачити, в обох випадках існує залежність ймовірності випромінювання від Z².

Також, на вигляд формул, що описують гальмівне випромінення впливає спотворення кулонівського поля електронними оболонками атома.

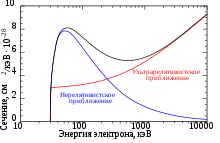
Під час розсіяння електрон може випромінити будь-яку кількість енергії, аж до його повної кінетичної енергії T, в залежності від того, наскільки близько від ядра він пройшов, і наскільки сильно змінилася його траєкторія. Таким чином, максимальна частота гальмівного випромінювання визначається рівнянням $\hbar \nu =T$, з якого випливає: $\nu ={\frac {eV}{\hbar }}$, де V — напруга, що прискорює електрон. Це рівняння називається лімітом Дуейна-Ганта. Це є однією з важливих відмінностей розподілу енергій, що передбачається класичною теорією, від того, що передбачає квантово-механічна — у класичній теорії гальмівне випромінювання охоплює весь спектр.

Кутовий розподіл випромінювання

Кутовий розподіл гальмівного випромінювання залежить від кінетичної енергії падаючих електронів. У випадку релятивістських електронів, напрямки вильоту фотонів переважно знаходяться у конусі, з кутом при вершині $\upsilon \approx {\frac {m_{e}c^{2}}{T_{e}}}$ (це значення є середнім кутом вильоту фотонів). Кутовий розподіл в такому випадку буде наступним :

$d\sigma (E,\theta )={\frac {A\cdot \theta d\theta }{\theta ^{2}+{\frac {m_{e}c^{2}}{E}}}}$

Для нерелятивістських електронів, фотони можуть випроміюватися як вперед, так і назад, їх кутовий розподіл пропорційний cos²θ, де θ — кут між напрямом вильоту фотона і траєкторією електрона, що гальмується.

Поляризація

Якщо електрон гальмується лінійно, то його випромінювання буде повністю поляризоване. Проте, гальмівне випромінювання у речовині продукується електронами, що рухаються по гіперболічних траєкторіях, а тому поляризоване лише частково. Чим ближче до ядра пролітає електрон, тим сильніше змінюється його траєкторія, а отже, тим більшою є компонента прискорення, що напрямлена в протилежну від руху сторону. Таким чином, є два випадки майже повної поляризації гальмівного випромінювання: коли електрон проходить дуже близько від ядра, і практично зупиняється (в цьому випадку вектори швидкості та гальмуючого поля практично паралельні), що відповідає зоні, близькій до короткохвильового ліміту фотонів, або коли він проходить відносно далеко від ядра (тоді вектори швидкості та поля перпендикулярні, тобто поляризація є від’ємною), що відповідає найменш енергетичним фотонам:. В проміжних випадках поляризація менша.

Загальна поляризація гальмівного випромінювання становить близько 50%.

Спектр

Залежність інтенсивності випромінення від енергії фотона, для налітаючих електронів різних енергій

Спектр гальмівного випромінювання неперервний, а його максимальна частота визначається енергією зарядженої частинки. Якщо електрон прискорити в потенціалі в десятки кіловольтів, то при гальмуванні такого електрона виникнуть електромагнітні хвилі в рентгенівському діапазоні.

Форма спектру є складною, але загальні принципи є наступними: частка фотонів заданої частоти зменшується з ростом частоти, і прямує до нуля при наближенні до максимального її значення. Для більш високоенергетичних електронів, доля фотонів, енергія яких є близькою до максимально можливої, зростає.

Хорошим наближенням спектру гальмівного випромінювання є формула Крамерса:

$I(\lambda )=KZ{\frac {\lambda -\lambda _{0}}{\lambda _{0}\lambda ^{3}}}$,

де λ₀ — мінімальна довжина хвилі випромінювання, а K — деякий коефіцієнт, що залежить від матеріалу мішені.

На практиці, через те, що поглинання низькоенергетичних фотонів у речовині є значно сильнішим, ніж високоенергетичних, спектр фотонів пригнічується у низькочастотній області.

Інтенсивність

При прольоті через шар речовини товщиною dx, що складається з атомів з зарядом Ze і масовим числом А, електрон випромінює деяку долю своєї енергії E_e, що виражається наступною емпіричною формулою:

$dE=-\left(1,4Z^{2}{\frac {5,2-{\frac {lnZ}{3}}}{A}}\right)E_{e}dx\cdot 10^{-3}$

де dx має розмірність г/см².

З формули видно, що енергія електронів і інтенсивність гальмівного випромінювання спадають експоненційно при заглибленні в мішень. Товщина шару речовини, при прольоті через яку енергія електрона зменшується в e разів називається радіаційною довжиною. Ця величина часто використовується для вимірювання товщини мішеней.

Оскільки гамма-випромінювання також поглинається у речовині, для максимізації інтенсивності випромінювання, товщина мішені має бути не дуже великою. Зазвичай, випромінювання досягає максимуму при товщині шару речовини в 1/3-1/4 від максимального пробігу.

Джерела

Рентгенівські трубки

У рентгенівських трубках, електрони розганяються електричним полем, після чого вдаряються у спеціальну металеву мішень. Під час зіткнень з атомами мішені, електрони гальмуються, і випромінюють фотони, в тому числі і в рентгенівському діапазоні. Не все випромінювання рентгенівських трубок є гальмівним — велика його частина припадає на характеристичне рентгенівське випромінювання — передачі енергії електрону, що переводить його на більш високу орбіталь, і подальше його повернення на нижній енергетичний рівень з випроміненням отриманої енергії.

Завдяки своїй простоті і доступності, ця схема є дуже вживаною для штучного отримання рентгенівських променів, і використовується в медицині і техніці, незважаючи на те, що її ККД досить низький — лише 3-8% енергії перетворюється на рентгенівське випромінювання.

Бета-розпад

Одним з продуктів бета-розпаду є бета-частинка — високоенергетичний електрон. При проходженні бета-частинок через речовину вони втрачають енергію через гальмівне випромінення, і цей канал є тим більшим, чим більшою є енергія частинки. Окрім звичайного гальмівного випромінювання, що утворюється при русі електрона в речовині (зовнішнє гальмівне випромінювання), існує інший підвид випромінювання, що характерне для бета-розпаду — внутрішнє гальмівне випромінювання, що складається з гама-квантів, які утворюються безпосередньо при бета-розпаді. Оскільки енергія бета-частинок є обмеженою, помітним гальмівне випромінення стає лише для дуже інтенсивних бета-випромінювачів.

Гальмівне випромінювання варто враховувати при розробці захисту від бета-радіації, адже гамма-промені мають значно більшу проникну здатність ніж бета-частинки, для захисту від яких достатньо металевого екрану товщиною в кілька міліметрів. Для захисту від високоенергетичних бета-частинок варто використовувати екрани з пластику або інших матеріалів, що складаються з елементів з низьким атомним номером, для зменшення ймовірності випромінювання високоенергетичних фотонів.

Тепловий рух

У плазмі атоми є іонізованими, а отже присутня велика кількість вільних носіїв заряду. Гальмівне випромінювання в такому випадку виникає при зіткненні електронів та іонів. Зі збільшенням температури, швидкості електронів і, відповідно, енергії фотонів зростають.

Якщо плазма є прозорою для випромінювання, то гальмівне випромінювання є ефективним способом її охолодження. Такий канал є основним для температур, вищих за 10 мільйонів кельвінів.

Саме таке випромінювання є основною причиною радіовипромінювання сонячної корони, планетарних туманностей і міжзоряного газу.

Електрон-електронне розсіяння

Електрон може розсіюватися і на електронних оболонках атомів. Це випромінювання є значно меншим, за те, що генерується при розсіянні на ядрах, оскільки заряд електрона складає лише e, тоді як енергія гальмівного випромінювання пропорційна квадрату заряду частинки-мішені. При енергіях падаючих електронів менших за 300 кеВ цим каналом можна нехтувати. Проте зі зростанням швидкості електронів, а також для легких елементів (заряд ядра яких є не таким великим, порівняно з зарядом електрона), наприклад при проходженні через повітря, його значимість зростає. Електрон-електронне гальмівне випромінювання є значним у деяких астрофізичних процесах, у хмарах плазми з температурою більшою за 10⁹ К.

Нуклонне гальмівне випромінювання

Як було сказано вище, інтенсивність гальмівного випромінення, що створюється протонами у кулонівському полі, у кілька мільйонів разів менша за випромінення, що створюється електронами, через те, що вона обернено пропорційна квадрату маси. Проте, нуклон-нуклонні сили значно більші за електромагнітні, а тому гальмівне випромінювання нуклонами було зафіксовано у ядерних реакціях, таких як

• p + n → ²H + γ

або

• p + ²H → ³He + γ

Фотони, що випромінюються у таких реакціях мають енергію в кілька МеВ.

Література

• В. Гайтлер. Радиационные процессы в первом приближении // Квантовая теория излучения. — 3. — М. : "Издательство иностранной литературы", 1956. — С. 280. — ISBN 5-4584-2739-4.
• Кузнецов Р.А. Нормированные спектры тормозного излучения для разных энергий электронов // Активационный анализ. — 2. — М. : АТОМИЗДАТ, 1974. — С. 111.
• Гелий Павлинский. Тормозное рентгеновское излучение // Основы физики рентгеновского излучения. — М. : Физматлит, 2007. — С. 47. — ISBN 5-4579-6651-8.
• Бочкарёв В.В. Применение радиоактивных изотопов // Получение и применение радиоактивных изотопов. — М. : Госатомиздат, 1962. — 288 с.
• И.Л. Кнунянц. Защита от излучений радиоактивных веществ // Краткая химическая энциклопедия. — М. : "Советская энциклопедия", 1962. — Т. 2. — С. 91. — ISBN 5-4582-6128-3.
• Исследование активных процессов в солнечной короне // Солнечно-земная физика. — М. : Физматлит, 2009. — 488 с. — ISBN 978-5-9221-1175-1.
• Michael F. L'Annunziata. Bremsstrahlung // Radioactivity: Introduction and History, From the Quantum to Quarks. — 2. — ELSEVIER, 2016. — 903 с. — ISBN 978-0-4446-3496-2.