Граф Клебша
| Граф Клебша | |
|---|---|
 | |
| Вершин | 16 |
| Ребер | 40 |
| Радіус | 2 |
| Діаметр | 2 |
| Обхват | 4 |
| Автоморфізм | 1920 |
| Хроматичне число | 4[1] |
| Число черг | 3 |
| Властивості | |
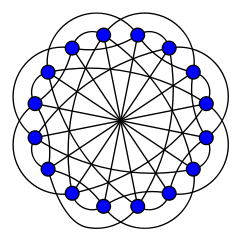
У теорії графів граф Клебша — один з двох взаємодоповняльних графів, що мають 16 вершин. Один з них має 40 ребер і є 5-регулярним графом, інший має 80 ребер і є 10-регулярним графом. 80-реберний варіант — це половинний граф куба[en] 5-го порядку. 1968 року Зайдель[de][2] назвав його графом Клебша, зважаючи на його зв'язок із конфігурацією прямих поверхні четвертого порядку, яку відкрив 1868 року німецький математик Альфред Клебш. 40-реберний варіант — це складений граф куба[en] 5 порядку. Він відомий також під назвою граф Грінвуда — Глізона після роботи Грінвуда і Глізона[3], в якій вони використали цей граф для обчислення числа Рамсея R(3,3,3) = 17[3][4][5].
Складаний граф куба[en] 5-го порядку (5-регулярний граф Клебша) можна побудувати, додавши ребра між протилежними вершинами графа 4-вимірного гіперкуба (В n-вимірному гіперкубі пара вершин протилежна, якщо найкоротша відстань між ними містить n ребер). Його можна побудувати також із графа 5-вимірного гіперкуба стягуванням кожної пари протилежних вершин.
Ще одна побудова, що дає той самий граф, полягає у створенні вершини для кожного елемента скінченного поля GF (16) і з'єднанні двох вершин ребром, якщо різниця відповідних елементів поля є кубом[6].
Половинний граф куба[en] 5-го порядку (10-регулярний граф Клебша) — це доповнення 5-регулярного графа. Його можна також побудувати з вершин 5-вимірного гіперкуба, з'єднавши пари вершин, між якими відстань Геммінга дорівнює рівно два. Ця побудова утворює дві підмножини по 16 вершин у кожній, не пов'язаних між собою. Обидва отриманих графи ізоморфні 10-регулярному графу Клебша.
5-регулярний граф Клебша є сильно регулярним графом 5-го степеня з параметрами [7]. Його доповнення, 10-регулярний граф Клебша, теж сильно регулярний[1][5].
5-регулярний граф Клебша є гамільтоновим, непланарним і не ейлеровим. Обидва графи є 5-вершинно зв'язними і 5-реберно-зв'язними. Підграф, породжений десятьма вершинами, які не є сусідами будь-якої вершини в цьому графі, ізоморфний графу Петерсена.
Ребра повного графа K16 можна розділити на три незв'язних копії 5-регулярного графа Клебша. Оскільки граф Клебша не містить трикутників, це показує, що існує триколірне розфарбування без трикутників ребер графа K16. Таким чином, число Рамсея R(3,3,3), що описує найменше число вершин у повному графі за триколірного розфарбовування без трикутників, не може бути меншим від 17. Грінвуд і Глізон використали цю побудову як частину свого доведення рівності R(3,3,3) = 17[3][8].
5-регулярний граф Клебша є графом Келлера розмірності два, і входить до сімейства графів, використовуваних для пошуку покриття евклідових просторів великої розмірності гіперкубами, що не мають спільних граней.
Характеристичний многочлен 5-регулярного графа Клебша — це . Отже, граф Клебша є цілим графом — його спектр складається тільки з цілих чисел[5]. Граф Клебша — єдиний граф із таким характеристичним многочленом.
5-регулярний граф Клебша є графом Келі з групою автоморфізмів порядку 1920, ізоморфною групі Коксетера . Як у будь-якому графі Келі, група автоморфізмів діє на його вершини транзитивно, роблячи його вершинно-транзитивним. Фактично він є симетричним графом, а тому він реберно-транзитивний і дистанційно-транзитивний.
-
Граф Клебша є гамільтоновим.
-
Ахроматичне число графа Клебша дорівнює 8.
-
Хроматичне число графа Клебша дорівнює 4.
-
Хроматичний клас графа Клебша дорівнює 5.
-
Побудова графа Клебша з графа гіперкуба.
- ↑ а б . Eric W. Weisstein. Clebsch Graph. From MathWorld — A Wolfram Web Resource. Архів оригіналу за 7 лютого 2009. Процитовано 13 серпня 2009.
- ↑ J. J. Seidel, Strongly regular graphs with (−1,1,0) adjacency matrix having eigenvalue 3, Lin. Alg. Appl. 1 (1968) 281—298.
- ↑ а б в R. E. Greenwood, Andrew Gleason. Combinatorial relations and chromatic graphs // Canadian Journal of Mathematics. — 1955. — Т. 7. — С. 1—7. — DOI:.
- ↑ A. Clebsch. Ueber die Flächen vierter Ordnung, welche eine Doppelcurve zweiten Grades besitzen // J. für Math. — 1868. — Т. 69. — С. 142—184.
- ↑ а б в The Clebsch Graph on Bill Cherowitzo's home page (PDF). Архів (PDF) оригіналу за 29 жовтня 2013. Процитовано 25 жовтня 2013.
- ↑ De Clerck, Frank (1997). Constructions and Characterizations of (Semi)partial Geometries. Summer School on Finite Geometries. с. 6. Архів оригіналу за 15 червня 2011. Процитовано 25 жовтня 2013.
- ↑ C. D. Godsil. Problems in algebraic combinatorics // Electronic Journal of Combinatorics[en]. — 1995. — Т. 2. — С. 3. Архівовано з джерела 24 лютого 2012. Процитовано 2009-08-13.
- ↑ Hugo S. Sun, M. E. Cohen. An easy proof of the Greenwood–Gleason evaluation of the Ramsey number R (3,3,3) // The Fibonacci Quarterly. — 1984. — Т. 22, вип. 3. — С. 235—238. Архівовано з джерела 29 вересня 2020. Процитовано 1 червня 2022.







