Мінімакс
Мінімакс (англ. minimax, нім. minimax n) — правило прийняття рішень, що використовується в теорії ігор, теорії прийняття рішень, дослідженні операцій, статистиці і філософії для мінімізації можливих втрат з тих, які особа, яка приймає рішення не може уникнути при розвитку подій за найгіршим для неї сценарієм. Критерій мінімаксу спочатку був сформульований в теорії ігор для гри двох осіб з нульовою сумою для випадків послідовних і одночасних ходів, згодом отримав розвиток у складніших іграх і прийнятті рішень в умовах невизначеності. З поняттям мінімаксу пов'язане поняття максиміна (значення мінімаксу не менше значення відповідного максиміну).
Теорія ігор[ред. | ред. код]
У теорії ігор стратегія мінімаксу це змішана стратегія, яка є одним з розв'язків гри нульовою сумою. В іграх з нульовою сумою стратегія мінімаксу є рівновагою Неша.
Теорема мінімаксу[ред. | ред. код]
У 1945 році Оскар Морґенштерн і Джон фон Нейман запропонували метод мінімаксу, який знайшов широке застосування.
Теорема мінімаксу стверджує
Для кожної гри для двох осіб з нульовою сумою та скінченним числом стратегій, існує таке значення V та змішані стратегії для кожного гравця, такі, що (а) Для будь-якої стратегії Гравця 2, Гравець 1 може гарантувати собі виграш V, і (б) Для будь-якої стратегії Гравця 1, Гравець 2 може гарантувати собі виграш (-V).
Це рівнозначно тому, що стратегія Гравця 1 гарантує його виграш V, незалежно від стратегії гравця 2, а також що Гравець 2 теж може гарантувати собі виграш -V. Назва алгоритм мінімаксу виникла тому, що кожен гравець мінімізує максимально можливу винагороду для іншого гравця, так як гра з нульовою сумою, він також максимізує свою винагороду.
Приклад[ред. | ред. код]
| Б обирає Б1 | Б обирає Б2 | Б обирає Б3 | |
|---|---|---|---|
| A обирає A1 | +3 | −2 | +2 |
| A обирає A2 | −1 | 0 | +4 |
| A обирає A3 | −4 | −3 | +1 |
Приклад гри з нульовою сумою, де А і Б роблять ходи, показує рішення мінімаксу. Припустимо, що у кожного гравця є три варіанти і розглянемо матрицю для А, яка відображена справа. Припустимо, що платіжна матриця для Б така ж матриця зі зворотним знаком (наприклад, якщо вибір A1 і Б1, то Б платить А 3). Тоді вибір мінімаксу А є A2 з найгіршим результатом - платити 1, у той час як простий вибір мінімаксу для Б є Б2 з найгіршим результатом — нічого не платити. Однак це рішення не є стійким, тому що якщо Б вважає, що А вибере А2, то Б вибере Б1, щоб отримати 1, а якщо A вважає, що Б вибере Б1, то А вибере A1, щоб отримати 3, тому Б вибере Б2, і врешті-решт обидва гравці усвідомлюють труднощі зробити вибір. Таким чином, потрібна більш стабільна стратегія.
Деякі варіанти гірші за інші, і можуть бути усунені: А не буде обирати А3, тому що А1 або А2 дають кращий результат, незалежно від того, що обере Б ; Б не буде вибирати Б3, так як і Б1, і Б2 дають кращі результати, незалежно від того, що обере А.
А може уникнути того, щоб робити очікувані виплати більш ніж на 1/3 обираючи A1 з імовірністю 1/6 і А2 з імовірністю 5/6, незалежно від того, що вибирає Б. Б може забезпечити очікуваний приріст, принаймні на 1/3 за допомогою випадкової стратегії вибору Б1 з імовірністю 1/3 і Б2 з імовірністю 2/3, незалежно від того, що вибирає А. Ці мінімаксні стратегії тепер є стабільними і не можуть бути поліпшені.
Максимін[ред. | ред. код]
У теорії ігор максимін часто відрізняється від мінімаксу. Мінімакс використовується в іграх з нульовою сумою, щоб підкреслити мінімізацію максимального виграшу противника. У грі з нульовою сумою, це ідентично максимізації свого виграшу. «Максимін» — це термін, який зазвичай використовується для ігор з ненульовою сумою, щоб описати стратегію, яка максимізує власну мінімальну винагороду. У іграх з ненульовою сумою це не те ж саме, що мінімізація максимальної винагороди противника, і не стратегія рівноваги Неша.
Комбінаторна теорія ігор[ред. | ред. код]
У комбінаторній теорії ігор є алгоритм мінімаксу для ігрових рішень. Простий варіант алгоритму мінімаксу, зазначений нижче, стосується ігор, таких як гра в хрестики-нулики, де кожен гравець може виграти, програти або зіграти в нічию. Якщо гравець А може виграти за один хід, то це і є його найкращий хід. Якщо гравець Б знає, що певний крок призведе до ситуації, коли гравець А може виграти в один хід, в той час інший крок призведе до ситуації, коли гравець А може, за найсприятливіших обставин, претендувати на нічию, то найкращий хід гравця Б є один з тих, що веде до нічиї. Наприкінці гри легко побачити, які кроки є «найкращими». Алгоритм мінімаксу допомагає знайти найкращий хід, працюючи в зворотному порядку від кінця гри. На кожному кроці він припускає, що гравець А намагається максимізувати шанси на перемогу, а на наступний хід гравець Б намагається звести ці шанси до мінімуму (тобто максимізувати власні шанси гравця Б на перемогу).
Алгоритм мінімаксу з альтернативним рухом[ред. | ред. код]
Мінімаксний алгоритм рекурсивний алгоритм для вибору наступного кроку для ігор з n гравцями, як правило, двох гравців. Евристична оцінка пов'язана з кожним положенням або станом гри. Це значення обчислюється за допомогою евристичної функції, і це показує, як добре було б для гравця досягти цієї позиції. Потім гравець робить хід, який максимізує мінімальне значення позиції в результаті можливих наступних ходів суперника. Якщо черга А робити хід, то А дає оцінку для кожного зі своїх ходів.
Можливий спосіб розрізнення полягає в призначенні для певної гри характеристик для А як +1 і для Б як -1. Альтернативою є використання правила, що якщо в результаті руху А є безпосередня перемога А, то призначити певну додатну оцінку, а якщо призведе до безпосередньої перемоги Б , певну від'ємну оцінку. Значення А для будь-якого іншого ходу є мінімум значень, отриманих від кожного з можливих ходів Б. З цієї причини, А називають максимізуючим гравцем і Б називають мінімізуючим гравцем, звідси і назва алгоритму мінімаксу. Алгоритм призначить певне додатне чи від'ємне значення для будь-якого стану, оскільки значення кожної позиції буде знаходитись із значень деяких остаточних виграшних чи програшних позицій. Часто це стає можливим тільки в самому кінці складних ігор, таких як шахи або ґо, так як це не обчислювально дивитися в майбутнє аж до завершення гри, за винятком ситуацій, близьких до кінця гри.
Але це може бути знайдено, якщо ми зможемо поставити евристичну функцію оцінки, яка дає значення для некінцевих станів гри без урахування всіх можливих наступних станів. Тоді ми можемо ввести обмеження для мінімаксного алгоритму - дивитися тільки на певну кількість ходів вперед. Це число називається "глибиною пошуку".
Використання алгоритмів евристичного пошуку для пошуку на графі виграшної стратегії в складніших задачах та іграх (шашки, шахи) не реальний. За деякими оцінками ігрове дерево гри в шашки містить 1040 вершин, в шахах 10120 вершин. Якщо при грі в шашки для однієї вершини потрібно 1/3 наносекунди, то всього ігрового часу буде потрібно 1021 століть. У таких випадках вводяться штучні умови зупинки, засновані на таких факторах, як найбільша допустима глибина вершин у дереві пошуку або обмеження на час і обсяг пам'яті. Наприклад, шаховий комп'ютер Deep Blue (який виграв у Гарі Каспарова) для глибини у 12 ходів перебравши усі можливі стани, тоді застосував евристичні функції оцінки.
Алгоритм може розглядатися як дослідження вузла дерева варіантів. Фактором розгалуження дерева є середнє число дітей для кожного вузла (тобто середня кількість можливих ходів для будь-якого стану). Число вузлів зазвичай зростає експоненційно з глибиною пошуку. Число вузлів, які аналізуються, є приблизний коефіцієнт розгалуження зведений в ступінь глибини пошуку. Тому непрактично повністю проаналізовувати такі ігри, як шахи, використанням мінімаксного алгоритму.
Продуктивність простого алгоритму мінімаксу може бути значно покращено, не впливаючи на результат, за допомогою відсічення альфа-бета. Теоретично, це еквівалент алгоритму мінімаксу, за допомогою якого завжди виходить такий же результат, але помітно швидше, так як цілі частини дерева виключаються без проведення аналізу. В основі цієї процедури лежить ідея Дж. Маккарті про використання двох змінних, позначених α і β (1961 рік).
Інші методи евристичних відсікань також можуть бути використані, але не всі з них гарантовано дають той же результат, що й алгоритм без відсікань.
Простий алгоритм мінімаксу може бути тривіально змінений, щоб додатково повертати саму стратегію разом з результатом мінімаксу.
Приклад Lua[ред. | ред. код]
function minimax(node, depth)
if depth <= 0 then
-- positive values are good for the maximizing player
-- negative values are good for the minimizing player
return objective_value(node)
end
-- maximizing player is (+1)
-- minimizing player is (-1)
local alpha = -node.player * INFINITY
local child = next_child(node, nil)
while child do
local score = minimax(child, depth-1)
alpha = node.player==1 and math.max(alpha, score) or math.min(alpha, score)
child = next_child(node, child)
end
return alpha
end
Приклад C++[ред. | ред. код]
int MinMax(int depth)
{
int best = -INFINITY;
int val;
if (depth <= 0)
return Evaluate();
GenerateLegalMoves();
while (MovesLeft()) {
MakeNextMove();
val = -MinMax(depth - 1);
UnmakeMove();
if (val > best)
best = val;
}
return best;
}
Приклад Java pseudo-code[ред. | ред. код]
abstract class Minimax // Java pseudo-code
{
protected static final Layout layout = Layout.getTheLayout() // Singleton
protected abstract int minOrMax( int s1, int s2 ) // min() or max()
protected abstract Minimax makeMinimax() // Factory Method
protected abstract int getGameOverScore() // WIN, LOSE, or TIE
protected abstract int getWorstScore() // INFINITY or MINUS_INFINITY
// ...
public int minimax( int depth ) // Template Method
{
if( layout.isGameOver() )
{
return getGameOverScore()
}
if( depth == 0 )
{
return evaluateBoard() // Maybe Random
}
Minimax child = makeMinimax()
int bestSoFar = getWorstScore()
Vector moves = layout.getAllLegalMoves()
Enumeration moveEnum = moves.elements()
while( moveEnum.hasMoreElements() )
{
Move nextMove = (Move) moveEnum.nextElement()
layout.processMove( nextMove ) // Must undo this
int score = child.minimax( depth - 1 ) // !
bestSoFar = minOrMax( bestSoFar, score )
layout.unprocessMove( nextMove )
}
return bestSoFar
}
Псевдокод[ред. | ред. код]
Нижче представлений псевдокод для Negamax версії алгоритму мінімаксу (використовуючи евристичну оцінку для припинення на заданій глибині).
function integer minimax(node, depth)
if node is a terminal node or depth <= 0:
return the heuristic value of node
α = -∞
for child in node: # evaluation is identical for both players
α = max(α, -minimax(child, depth-1))
return α
Приклад[ред. | ред. код]
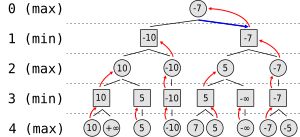
Припустимо, що в грі є максимум два можливих кроки для кожного гравця на кожен хід. Алгоритм генерує дерево праворуч, де кола є ходи максимізуючого гравця, а квадрати являють собою ходи суперника ( мінімізуючий гравець ). Через обмеженість обчислювальних ресурсів, як описано вище, дерево обмежено на 4 кроки уперед.
Алгоритм оцінює кожен вузол за допомогою евристичних функцій оцінки, отримані значення показано на малюнку. Ходи, де максимізуючий гравець виграє, оцінені як додатна нескінченність, в той час як кроки, які приведуть до перемоги мінімізуючого гравця, оцінені як від'ємна нескінченність. На рівні 3 алгоритм буде вибирати, для кожного вузла, найменше зі значень його дочірніх вузлів, і призначить це значення тому ж вузлу (наприклад, вузол зліва буде вибирати мінімальне з "10" і "+ ∞", тому призначить собі значення "10"). Наступний крок, на рівні 2, полягає у виборі найбільшого значення для кожного вузла серед його дочірніх вузлів. Знову ж таки, кожне значення присвоюється кожному батьківському вузлу. Алгоритм продовжує оцінки максимального і мінімального значень дочірніх вузлів по черзі, аж поки не досягне кореневого вузла, де він вибирає хід з найбільшим значенням (представлено на малюнку синьою стрілкою). Це крок, який гравець повинен зробити для того, щоб звести до мінімуму максимально можливої втрати.
Максимін в філософії[ред. | ред. код]
У філософії термін «максиміна» часто використовується в контексті «Теорії справедливості» Джона Роулза, де він ставиться до нього (Rawls (1971, с. 152)) в контексті принципу різниці. Роулз визначив цей принцип як правило, яке свідчить, що соціальні і економічні нерівності повинні бути організовані так, що «вони повинні мати найбільшу користь найменш сприятливому члену суспільства». Іншими словами, нерівномірний розподіл може бути тільки тоді, коли він максимізує мінімальну користь тих, хто має низький рівень добробуту (які він називає «сировинні товари»).
| |||||||||||||||||