Перенавчання
| Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. (грудень 2016) |


У статистиці та машинному навчанні одним із найпоширеніших завдань є допасовування «моделі» до набору тренувальних даних таким чином, щоби уможливити здійснення надійних передбачень на загальних даних, на яких не здійснювалося тренування. При перенавчанні (англ. overfitting) статистична модель описує випадкову похибку або шум, замість взаємозв'язку, що лежить в основі даних. Перенавчання виникає тоді, коли модель є занадто складною, такою, що має занадто багато параметрів відносно числа спостережень. Перенавчена модель має погану передбачувальну[en] продуктивність, оскільки вона занадто сильно реагує на другорядні відхилення в тренувальних даних.
Можливість перенавчання існує тому, що критерій, який застосовується для тренування моделі, відрізняється від критерію, який застосовується для оцінки її ефективності. Зокрема, модель зазвичай тренують шляхом максимізації її продуктивності на якомусь наборі тренувальних даних. Проте її ефективність визначається не її продуктивністю на тренувальних даних, а її здатністю працювати добре на даних небачених. Перенавчання стається тоді, коли модель починає «запам'ятовувати» тренувальні дані, замість того, щоби «вчитися» узагальненню з тенденції. Як крайній приклад, якщо число параметрів є таким же, або більшим, як число спостережень, то проста модель або процес навчання може відмінно передбачувати тренувальні дані, просто запам'ятовуючи їх повністю, але така модель зазвичай зазнаватиме рішучої невдачі при здійсненні передбачень про нові або небачені дані, оскільки ця проста модель взагалі не навчилася узагальнювати.
Потенціал перенавчання залежить не лише від кількостей параметрів та даних, але й від відповідності структури моделі формі даних, та величини похибки моделі в порівнянні з очікуваним рівнем шуму або похибки в даних.
Навіть коли допасована модель не має надмірного числа параметрів, слід очікувати, що допасований взаємозв'язок працюватиме на новому наборі даних не так добре, як на наборі, використаному для допасовування.[1] Зокрема, значення коефіцієнту детермінації відносно первинних тренувальних даних скорочуватиметься[en].
Щоби уникати перенавчання, необхідно використовувати додаткові методики (наприклад, перехресне затверджування, регуляризацію, ранню зупинку, обрізку[en], баєсові апріорні параметрів або порівняння моделей), які можуть вказувати, коли подальше тренування не даватиме кращого узагальнення. Основою деяких методик є або (1) явно штрафувати занадто складні моделі, або (2) перевіряти здатність моделі до узагальнення шляхом оцінки її продуктивності на наборі даних, не використаному для тренування, який вважається наближенням типових небачених даних, з якими стикатиметься модель.
Гарною аналогією перенавчання задачі є уявити дитину, яка намагається вивчити, що є вікном, а що не є вікном, ми починаємо показувати їй вікна, і вона виявляє на початковому етапі, що всі вікна мають скло та раму, і через них можна дивитися назовні, деякі з них може бути відчинено. Якщо ми продовжимо показувати ті самі вікна, то дитина може також зробити помилковий висновок, що всі вікна є зеленими, і що всі зелені рами є вікнами. Перенавчаючись таким чином цієї задачі.
Машинне навчання[ред. | ред. код]
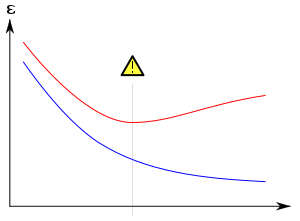
Зазвичай алгоритм навчання тренується з використанням деякого набору «тренувальних даних»: зразкових ситуацій, для яких бажаний вихід є відомим. Метою є, щоби алгоритм також добре працював над передбаченням виходу при подаванні «перевірних даних», які не траплялися під час його тренування.
Перенавчання є застосуванням моделей або процедур, які порушують лезо Оккама, наприклад, включаючи більше регульованих параметрів, ніж є зрештою оптимально, або використовуючи складніший підхід, ніж є зрештою оптимально. Для прикладу завеликого числа регульованих параметрів розгляньмо такий набір даних, де тренувальні дані для y може бути адекватно передбачено лінійною функцією двох залежних змінних. Така функція вимагає лише трьох параметрів (відсікання та двох нахилів). Заміна цієї простої функції новою, складнішою квадратичною функцією, або новою, складнішою лінійною функцією від понад двох залежних змінних, несе ризик: лезо Оккама значить, що будь-яка задана складна функція є апріорі менш імовірною за будь-яку задану просту функцію. Якщо цю нову, складнішу функцію обрано замість простої функції, і якщо не було достатньо великої користі для допасовування до тренувальних даних, щоби протиставити її підвищенню складності, то нова складніша функція «перенавчається» даних, і складна перенавчена функція, швидше за все, працюватиме гірше на перевірних даних за межами тренувального набору, ніж простіша функція, навіть якщо складніша функція працювала добре, або навіть краще, на наборі тренувальному.[2]
При порівнянні різних типів моделей складність не можна вимірювати виключно підрахунком того, скільки параметрів існує в кожній з моделей; мусить також розглядатися й виразність кожного з параметрів. Наприклад, є нетривіальним порівнювати безпосередньо складності нейронної мережі (яка може відстежувати криволінійні взаємозв'язки) з m параметрами, та регресійної моделі з n параметрами.[2]
Перенавчання є особливо ймовірним в тих випадках, коли навчання виконувалося занадто довго, або коли тренувальні зразки є рідкісними, що спричиняє допасовування до дуже особливих випадкових ознак тренувальних даних, які не мають причинного взаємозв'язку[en] з цільовою функцією[en]. В процесі цього перенавчання продуктивність на тренувальних зразках продовжує підвищуватися, тоді як продуктивність на небачених даних стає гіршою.
Як простий приклад розгляньмо базу даних роздрібних купівель, яка включає придбану позицію, покупця, та дату й час купівлі. Нескладно побудувати модель, яка ідеально допасовується до тренувального набору із застосуванням дати й часу купівлі, щоби передбачувати інші ознаки; але ця модель взагалі не узагальнюватиметься на нові дані, оскільки ті минулі часи вже ніколи не настануть.
Як правило, кажуть, що алгоритм навчання перенавчається відносно простішого, якщо він є точнішим у допасовуванні до відомих даних (розумність заднім числом), але менш точним у передбачуванні нових даних (далекоглядність). Перенавчання можна інтуїтивно розуміти з точки зору тієї обставини, що інформацію з усього минулого досвіду може бути поділено на дві групи: інформацію, яка стосується майбутнього, і недоречну інформацію («шум»). За всіх інших рівних умов, що складнішим для передбачування є критерій (тобто, що вищою є невизначеність), то більше шуму, який треба ігнорувати, міститься в минулій інформації. Задача полягає у визначенні того, яку частину ігнорувати. Алгоритм навчання, який знижує шанси допасовування до шуму, називається надійним.
Наслідки[ред. | ред. код]
Найочевиднішим наслідком перенавчання є погана продуктивність на перевірному наборі даних. До інших негативних наслідків належать:[2]
- Перенавчена функція схильна вимагати більше інформації про кожен елемент перевірного набору даних, ніж функція оптимальна; збирання цих додаткових непотрібних даних може бути витратним або схильним до помилок, особливо якщо кожну окрему частину інформації потрібно збирати за допомогою людського спостереження та введення даних вручну.
- Складніша, перенавчена функція схильна бути менш переносною, ніж проста. Як одна з крайностей, лінійна регресія з однією змінною є настільки переносною, що, за потреби, може навіть здійснюватися вручну. На протилежній крайності знаходяться моделі, які може бути відтворено лише точним дублюванням цілісної постановки первинного розробника, що ускладнює повторне використання або наукове відтворення.
Регресія[ред. | ред. код]
Перенавчання також є проблемою і за межами машинного навчання, у широкому вивченні регресії, включно із регресією, здійснюваною «вручну». В крайньому випадку, якщо є змінних у лінійній регресії з точками даних, то допасована лінія проходитиме точно через всі точки.[3] Існує безліч емпіричних правил для визначення необхідного числа спостережень на кожну незалежну змінну, включно з 10[4] та 10-15.[5]
Недонавчання[ред. | ред. код]
Недонавчання трапляється тоді, коли статистична модель або алгоритм машинного навчання не можуть схопити тенденцію, що лежить в основі даних. Воно трапляється тоді, коли модель або алгоритм не достатньо допасовується до даних. Недонавчання трапляється тоді, коли модель або алгоритм демонструють низьку дисперсію, але високий зсув (на противагу протилежному перенавчанню з високою дисперсією та низьким зсувом). Часто воно є результатом занадто простої моделі.[6]
Див. також[ред. | ред. код]
- Компроміс зсуву та дисперсії
- Допасовування кривої[en]
- Просіювання даних
- Лезо Оккама
- Обирання моделі
- ВЧ-розмірність — вимірює складність моделі навчання. Більша ВЧ-розмірність означає вищий ризик перенавчання.
Примітки[ред. | ред. код]
- ↑ Everitt B.S. (2002) Cambridge Dictionary of Statistics, CUP. ISBN 0-521-81099-X (стаття «Shrinkage») (англ.)
- ↑ а б в Hawkins, Douglas M. «The problem of overfitting.» Journal of chemical information and computer sciences 44.1 (2004): 1-12. (англ.)
- ↑ Martha K. Smith (13 червня 2014). Overfitting. University of Texas at Austin. Процитовано 31 липня 2016. (англ.)
- ↑ Draper, Norman R.; Smith, Harry (1998). Applied regression analysis, 3rd Edition. New York: Wiley. ISBN 978-0471170822. (англ.)
- ↑ Jim Frost (3 вересня 2015). The Danger of Overfitting Regression Models. Процитовано 31 липня 2016. (англ.)
- ↑ Cai, Eric (20 березня 2014). Machine Learning Lesson of the Day – Overfitting and Underfitting. StatBlogs. Архів оригіналу за 29 грудня 2016. Процитовано 31 грудня 2016. (англ.)
Література[ред. | ред. код]
- Leinweber, D. J. (2007). Stupid Data Miner Tricks. The Journal of Investing. 16: 15—22. doi:10.3905/joi.2007.681820. (англ.)
- Tetko, I. V.; Livingstone, D. J.; Luik, A. I. (1995). Neural network studies. 1. Comparison of Overfitting and Overtraining (PDF). J. Chem. Inf. Comput. Sci.[en]. 35 (5): 826—833. doi:10.1021/ci00027a006. (англ.)
Посилання[ред. | ред. код]
- Overfitting: when accuracy measure goes wrong — ввідний відео-посібник. (англ.)
- The Problem of Overfitting Data (англ.)
- CSE546: Linear Regression Bias / Variance Tradeoff (англ.)
