Проєктивне перетворення
Проєктивне перетворення проєктивної площини — це перетворення, що переводить прямі в прямі.
Визначення[ред. | ред. код]
Проєктивне перетворення — це взаємно-однозначне відображення проєктивного простору на себе, яке зберігає відношення порядку частково впорядкованої множини всіх підпросторів.
Проєктивне перетворення прямої — бієктивне перетворення прямої, що переводить гармонійну четвірку точок в гармонійну четвірку точок.
Проєктивне перетворення площини — це взаємно-однозначне відображення проєктивної площини на себе, при якому для будь-якої прямої образ також є прямою.
Властивості[ред. | ред. код]
- Проєктивне перетворення зберігає подвійне відношення.
- Проєктивне перетворення є взаємно однозначним відображенням множини точок проєктивної площини, а також є взаємно однозначним відображенням множини прямих.
- Відображення, зворотне проєктивному, є проєктивним відображенням. Композиція проєктивних відображень є проєктивним відображенням. Таким чином, множина проєктивних відображень утворює групу.
- Центральне проєктування — частковий випадок проєктивного перетворення.
- Афінне перетворення є частковим випадком проєктивного.
- Кожна пряма площини при проєктивному перетворенні площини відображається проєктивно на деяку пряму. Кожен пучок променів площини проєктивно відображається на пучок променів.
- Проєктивне перетворення прямої визначається заданням трьох пар відповідних за відображенням точок. Це твердження називають іноді основною теоремою проєктивної геометрії.
- Проєктивне перетворення площини визначається заданням чотирьох пар відповідних за відображенням точок, причому ніякі три точки з четвірки образів або прообразів не лежать на одній прямій. При нетотожному відображенні кількість нерухомих точок не більша трьох.
- Кожне проєктивне перетворення площини задається оборотним лінійним перетворенням відповідного їй тривимірного простору. В однорідних координатах воно подається рівняннями:
причому .
Перспектива[ред. | ред. код]
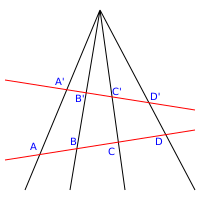
Нехай на проєктивній площині є 2 різні прямі і точка O, що не належить їм. Перспективним відображенням[en] прямої на пряму з центром O називається відображення , де для довільної точки точка знаходиться як перетин і . Це відображення позначається так: що читається « переводиться в пряму перспективним відображенням з центром O» або так: що читається «точки переводяться перспективним відображенням з центром в O в точки ».
Перспективне відображення бієктивне, зберігає точку перетину прямих і зберігає подвійне відношення четвірки точок.
Будь-яке проєктивне відображення прямої на пряму може бути подане як композиція перспективних відображень. Проєктивне відображення позначається
Інволюція[ред. | ред. код]
Проєктивне перетворення називається інволюцією, якщо для будь-якої точки P правильно, що .
Якщо — інволюція, то .
Якщо проєктивне перетворення прямої має хоча б одну таку точку P, що , то — інволюція.
Якщо нетотожна інволюція проєктивної прямої має нерухомі точки, то їх кількість дорівнює або двом, або нулю. Інволюція, що має 2 нерухомі точки, називається гіперболічною. Гіперболічна інволюція переставляє місцями точки, гармонійно спряжені відносно нерухомих точок. Інволюція, яка не має нерухомих точок, називається еліптичною.
Інволюція визначається заданням двох пар відповідних точок.
Три пари протилежних сторін повного чотирикутника перетинають будь-яку пряму (що не проходить через вершину) в трьох парах точок однієї інволюції (це твердження називають теоремою Дезарга, хоча її походження можна віднести до леми IV «Поризмів» Евкліда в VII томі «Математичної колекції» Паппа Александрійського).
Колінеації і кореляції[ред. | ред. код]
Колінеацією називається перетворення, що переводить точки в точки, прямі в прямі і зберігає відношення інцидентності точок і прямих, а також подвійне відношення будь-якої четвірки колінеарних точок. Колінеації утворюють групу. Вимога збереження подвійного відношення четвірки колінеарних точок надлишкова, але це складно довести. Колінеації розглядають разом з кореляціями — перетвореннями проєктивної площини, що переводять точки в прямі, а прямі в точки і зберігають відношення інцидентності. Приклад кореляції — полярна взаємність, тобто відображення, що переводить точку в її поляру відносно конічного перерізу, а пряму — в її полюс.
Гомологія[ред. | ред. код]
Гомологією називається нетотожна колінеація, для якої існує поточково нерухома пряма p, яка називається віссю гомології.
Для будь-якої гомології існує нерухома точка P (центр гомології), що володіє тією властивістю, що будь-яка інцидентна їй пряма нерухома. Крім центру P і точок осі p гомологія нерухомих точок не має. Якщо , то гомологія називається параболічною, інакше — гіперболічною.
При гомології площини точка і її образ лежать на одній прямій з центром гомології, а пряма і її образ перетинаються на осі гомології.
Гомологію можна задати центром, віссю і парою відповідних прямих. Гомологію можна також задати центром, віссю і т. зв. константою гомології, відмінною від .
Див. також[ред. | ред. код]
Література[ред. | ред. код]
- Д. А. Граве. Гомография // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп. т.). — СПб., 1890—1907. (рос. дореф.)
- П. С. Александров. Курс аналитической геометрии и линейной алгебры. — М. : Наука, 1979.
- Р. Хартсхорн. Основы проективной геометрии. — М. : Мир, 1970.
- Х. С. М. Кокстер. Действительная проективная плоскость / под ред. проф. А. А. Глаголева — М., 1959.
- Р. Курант, Г. Роббинс. Что такое математика?
- Н. В. Ефимов[ru]. Высшая геометрия. — ФизМатЛит, 2003.
- С. Л. Певзнер. Проективная геометрия. Учебное пособие по курсу "Геометрия" для студентов- заочников II-III курсов физико-математических факультетов. — М. : Просвещение, 1980.
| Це незавершена стаття з геометрії. Ви можете допомогти проєкту, виправивши або дописавши її. |























