Граф Гіґмана — Сімса

Граф Гіґмана — Сімса
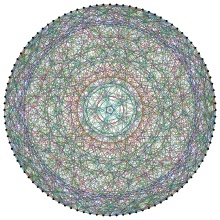Малюнок, що ґрунтується на побудові Поля Р. Гафнера
Названо на честь	Дональд Гіґман Чарльз Сімс
Вершин	100
Ребер	1100
Радіус	2
Діаметр	2
Обхват	4
Автоморфізм	88 704 000 (HS:2)
Властивості	сильно регулярний реберно-транзитивний гамільтонів ейлерів

Окремі частини побудови Гафнера.

Граф Гіґмана — Сімса — це 22-регулярний неорієнтований граф зі 100 вершинами і 1100 ребрами. Граф є унікальним сильно регулярним графом srg(100,22,0,6), тобто, ніяка сусідня пара вершин не має спільних сусідів і будь-яка несусідня пара вершин має шість спільних сусідів. Граф уперше побудував Меснер і перевідкрили 1968 року Дональд Дж. Гіґман і Чарльз Сімс як шлях визначення групи Гіґмана — Сімса і ця група є підгрупою з індексом два в групі автоморфізмів графа Гіґмана — Сімса.

Побудова починається з графа M₂₂, 77 вершин якого є блоками S(3,6,22) системи Штейнера W₂₂. Суміжні вершини визначаються як блоки, що не перетинаються. Цей граф сильно регулярний srg(77,16,0,4), тобто, будь-яка вершина має 16 сусідів, будь-які 2 суміжні вершини не мають спільних сусідів і будь-які 2 несуміжні вершини мають 4 спільні сусіди. Цей граф має M₂₂:2 як групу автоморфізмів, де M ₂₂ є групою Матьє.

Граф Гіґмана — Сімса формується додаванням 22 точок W₂₂ і 100-ї вершини C. Сусідами вершини C є ці 22 точки. Точка суміжна блоку тоді й лише тоді, коли вона належить блоку.

Граф Гіґмана — Сімса можна розбити на дві копії графа Гофмана — Сінглтона 352 способами.

Алгебричні властивості

Група автоморфізмів графа Гіґмана — Сімса є групою порядку 88 704 000, ізоморфною напівпрямому добутку групи Гіґмана — Сімса порядку 44 352 000 на циклічну групу порядку 2. Граф має автоморфізми, що переводять будь-яке ребро в будь-яке інше ребро, що робить граф Гіґмана — Сімса реберно-транзитивним.

Характеристичним многочленом графа Гіґмана — Сімса є $(x-22)(x-2)^{77}(x+8)^{22}$. Таким чином, граф Гіґмана — Сімса є цілим графом — його спектр складається виключно з цілих чисел. Граф є також єдиним графом з таким характеристичним многочленом, тому граф повністю визначається своїм спектром.

Всередині ґратки Ліча

Проєкція графа Гіґмана — Сімса в ґратку Ліча.

Граф Гіґмана — Сімса в природний спосіб розміщується всередині ґратки Ліча — якщо X, Y і Z — три точки в ґратці Ліча, такі, що відстані XY, XZ і YZ рівні $2,{\sqrt {6}},{\sqrt {6}}$ відповідно, то існує рівно 100 точок T ґратки Ліча, таких, що всі відстані XT, YT і ZT рівні 2, і якщо ми з'єднаємо дві такі точки T і T′, коли відстань між ними дорівнює ${\sqrt {6}}$, отриманий граф буде ізоморфним графу Гіґмана — Сімса. Більш того, множина всіх автоморфізмів ґратки Ліча (тобто рухів евклідового простору, що зберігають її), що зберігають точки X, Y і Z, є групою Гіґмана — Сімса (якщо ми дозволимо обмін X і Y, отримаємо розширення всіх автоморфізмів графа порядку 2). Це показує, що група Гіґмана — Сімса виявляється всередині груп Конвея Co₂ (з розширенням порядку 2) і Co₃, а отже, також усередині групи Co₁.

Див. також

• Граф Гевірца

Література

• Hafner P. R. On the Graphs of Hoffman–Singleton and Higman–Sims // the Electronic Journal of Combinatorics. — 2004. — Т. 11, вип. 1. — С. R77(1–32).
• Dale Marsh Mesner. An investigation of certain combinatorial properties of partially balanced incomplete block experimental designs and association schemes, with a detailed study of designs of Latin square and related types. — Department of Statistics, Michigan State University, 1956. — (Doctoral Thesis)
• Donald G. Higman, Charles C. Sims. A simple group of order 44,352,000 // Mathematische Zeitschrift. — 1968. — Т. 105, вип. 2. — С. 110–113. — DOI:10.1007/BF01110435.
• Brouwer A. E., Haemers W. H. The Gewirtz Graph: An Exercise in the Theory of Graph Spectra // Euro. J. Combin. — 1993. — Вип. 14.
• John H. Conway, Neil J. A. Sloane. chapter 10 (John H. Conway, "Three Lectures on Exceptional Groups"), §3.5 ("The Higman–Sims and McLaughlin groups") // Sphere Packings, Lattices and Groups. — 3rd. — Springer-Verlag, 1998. — (Grundlehren der mathematischen Wissenschaften) — ISBN 0-387-98585-9.