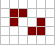
Натюрморт (конфігурація клітинного автомата)
Натюрморт — клас конфігурацій у «Житті» — створеного Конвеєм моделі клітинного автомата.
Натюрморти — конфігурації «Життя» або іншого клітинного автомата, які не змінюються в процесі еволюції[1]. Іншими словами, натюрморт є осцилятором періоду 1[2][3][4].
Існує декілька близьких за змістом термінів, що означають конфігурації, які не змінюються в процесі еволюції (конфігурації, що є власними батьками). Відмінності між ними пов'язані з відповіддю на наступні питання:
- Чи вважається натюрмортом конфігурація, що складається з двох незалежних натюрмортів (наприклад, двох блоків на досить великій відстані один від одного)?[5]
- Чи вважається натюрмортом конфігурація, яка складається з двох частин, будь-яку з яких можна видалити так, що друга частина залишиться батьком собі?
В існуючих словниках і онлайн-енциклопедіях[6][7][4][8] наводяться наступні визначення:
- Стійкий зразок (англ. stable pattern) — об'єкт, який є власним батьком[2][3];
- Натюрморт (англ. still life, strict still life) — стійкий об'єкт, що є кінцевим і непорожнім, який не може бути розділений на дві стійкі частини[9][10][8];
- Псевдонатюрморт (англ. pseudo still life) — стійкий об'єкт, що не є натюрмортом, в якому присутня хоч би одна мертва клітина, що має більше трьох сусідів всього, але менше трьох сусідів у кожному із складових об'єкт-натюрмортів[11][12][8].
Точне визначення «стійкості» представляє інтерес в контексті перерахування натюрмортів: наприклад, згідно з приведеними визначеннями, кількість стійких конфігурацій розміру 8 (тобто таких, що складаються з 8 живих клітин) в «Житті» нескінченно, оскільки пара блоків на будь-якій відстані один від одного є стійким; проте, кількість натюрмортів обмеженого розміру вважається кінцевою[6][7][8].
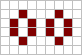 |
Псевдонатюрморт у «Житті». Віддаленість одного з островів не впливає на стабільність другого острова. |
 |
«Строгий» натюрморт. Стабільність кожного з островів залежить від наявності другого острова. |
Відоме число натюрмортів і псевдонатюрмортів розміру не вище 24 клітин[11][12][8].
Задача визначення типу стійкості конфігурації (натюрморт, псевдонатюрморт) вирішується за поліноміальний час шляхом пошуку циклів у зв'язаному кососиметричному графі[13].
У «Житті» існує множина природних[14] натюрмортів.
Найбільш поширений натюрморт — блок[15][16][17] — конфігурація у формі квадрата 2 × 2. Два блоки, розміщені в прямокутнику 2 × 5, утворюють бі-блок — простий псевдонатюрморт. Блоки використовуються як складові частини у безлічі складних пристроїв, наприклад, до планерної рушниці Госпера[17].
Другий за поширенням натюрморт — вулик (англ. hive, beehive). Вулики часто виникають четвірками в конфігурації, що називається пасікою (англ. honey farm)[15][16][17].
 |
Третій по поширеностті натюрморт — коровай (англ. loaf). Короваї нерідко з'являються парами (англ. bi-loaf)[15][16][17]. В свою чергу, подвійні короваї також з'являються в парах, званих пекарнями (англ. bakery)[18].
 |
 |
Ящик (англ. tub) складається з чотирьох живих клітин в околиці фон Неймана центральної мертвої клітини. Додавання однієї живої клітини по діагоналі до центральної клітини перетворює ящик на човен (англ. boat), а додавання симетрично ще однієї клітини — на корабель (англ. ship)[19]. Природне подовження цих трьох конфігурацій дає баржу (англ. barge), довгий човен (англ. long-boat) і довгий корабель (англ. long-ship) відповідно. Подовження можна продовжувати скільки завгодно довго[16][6][7][17].
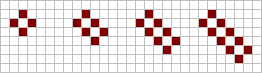 |
 |
 |
З двох човнів можна скласти ще один натюрморт — човниковий бант (англ. boat tie), а з двох кораблів — корабельний бант (англ. ship tie)[6][7].
 |
 |
|
Натюрморти можливо використати для модифікації або руйнування інших об'єктів. Пожирач (англ. eater) здатний знищити космічний корабель і відновитися після реакції. Відбивач (англ. reflector) замість знищення космічного корабля змінює його курс.
Відбивачі і пожирачі не обов'язково повинні бути натюрмортами.
| Пожирачі | ||||
|---|---|---|---|---|
|
Задача розміщення в області n × n натюрморта з максимальним числом клітин привертала до себе увагу програмістів як задача Програмування в обмеженнях[20][21][22][23][24]. При спрямування розміру області до нескінченності, живими можуть бути не більше 50 % клітин[25]. На обмежених квадратних областях можливо досягти більших щільностей. Так, максимальна щільність натюрморта в квадраті 8 × 8 дорівнює 36/64 = 0.5625 — цю щільність забезпечує зразок, що складається з дев'яти блоків[20] Для квадратів до 20 × 20 відомі оптимальні рішення[26][27].
| Натюрморти максимальної щільності у «Житті» | ||||
|---|---|---|---|---|
|
Число натюрмортів і псевдонатюрмортів в «Житті» відомо до розміра в 24 клітини[28][29][30].
| Число живих клітин | Число натюрмортів | Приклади |
|---|---|---|
| 1 | 0 | |
| 2 | 0 | |
| 3 | 0 | |
| 4 | 2 | блок, ящик |
| 5 | 1 | човен |
| 6 | 5 | баржа, авіаносець, вулик, корабель, змія |
| 7 | 4 | риболовний гачок, коровай, довгий човен |
| 8 | 9 | каное, манго, довга баржа, ставок |
| 9 | 10 | знак інтегралу |
| 10 | 25 | човниковий бант |
| 11 | 46 | |
| 12 | 121 | корабельний бант |
| 13 | 240 | |
| 14 | 619 | подвійний коровай |
| 15 | 1353 | |
| 16 | 3286 | |
| 17 | 7773 | |
| 18 | 19044 | |
| 19 | 45759 | пожирач-2 |
| 20 | 112243 | |
| 21 | 273188 | |
| 22 | 672172 | |
| 23 | 1646147 | |
| 24 | 4051711 |
- Николай Белюченко. Словарь Жизни. Архів оригіналу за 10 жовтня 2012. Процитовано 4 серпня 2017.
- Stephen A. Silver. Life Lexicon. Архів оригіналу за 26 травня 2013. Процитовано 4 серпня 2017.
- ↑ Більш строгі визначення див. у розділі «Термінологія».
- ↑ а б Устойчивый. Словарь Жизни.
- ↑ а б Stable. Life Lexicon. Архів оригіналу за 20 лютого 2009. Процитовано 4 серпня 2017.
- ↑ а б Eric Weisstein. Still Life. Treasure Trove of Life C.A. Процитовано 11 серпня 2013.
{{cite web}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання) - ↑ Якщо відповідь на це питання позитивна, то кількість натюрмортів з обмеженим числом клітин нескінченна.
- ↑ а б в г Николай Белюченко. Словарь Жизни (рос.). Архів оригіналу за 10 жовтня 2012. Процитовано 4 серпня 2017.
- ↑ а б в г Stephen A. Silver. Life Lexicon (англ.). Архів оригіналу за 26 травня 2013. Процитовано 4 серпня 2017.
- ↑ а б в г д Still life. ConwayLife.com. Процитовано 11 серпня 2013.
- ↑ Натюрморт. Словарь Жизни.
- ↑ Still life. Life Lexicon. Архів оригіналу за 20 лютого 2009. Процитовано 4 серпня 2017.
- ↑ а б Псевдонатюрморт. Словарь Жизни.
- ↑ а б Pseudo still life. Life Lexicon. Архів оригіналу за 3 грудня 2014. Процитовано 4 серпня 2017.
- ↑ Cook, Matthew (2003). Still life theory. New Constructions in Cellular Automata. Santa Fe Institute Studies in the Sciences of Complexity, Oxford University Press. с. 93—118.
- ↑ Природний зразок — об'єкт, який відносно часто виникає в процесі розвитку випадкової конфігурації.
- ↑ а б в Achim Flammenkamp. Top 100 of Game-of-Life Ash Objects. Процитовано 5 листопада 2008.
- ↑ а б в г Игра Жизнь (обзор Гарднера). Архів оригіналу за 18 жовтня 2012. Процитовано 11 серпня 2013.
- ↑ а б в г д Клумова И. Н. Игра «Жизнь» // Квант. — 1974. — № 9. — С. 26—30.
- ↑ Пекарня. Словарь Жизни.
- ↑ Не плутати з космічним кораблем.
- ↑ а б Bosch, R. A. (1999). Integer programming and Conway’s game of Life. SIAM Review. 41 (3): 594—604. doi:10.1137/S0036144598338252..
- ↑ Bosch, R. A. (2000). Maximum density stable patterns in variants of Conway’s game of Life. Operations Research Letters. 27 (1): 7—11. doi:10.1016/S0167-6377(00)00016-X..
- ↑ Smith, Barbara M. (2002). Principles and Practice of Constraint Programming - CP 2002. Lecture Notes in Computer Science. 2470. Springer-Verlag: 89—94. doi:10.1007/3-540-46135-3_27.
{{cite journal}}: Проігноровано|contribution=(довідка). - ↑ Bosch, Robert; Trick, Michael (2004). Constraint programming and hybrid formulations for three Life designs. Annals of Operations Research. 130 (1–4): 41—56. doi:10.1023/B:ANOR.0000032569.86938.2f..
- ↑ Cheng, Kenil C. K.; Yap, Roland H. C. (2006). Applying ad-hoc global constraints with the case constraint to still-life. Constraints. 11 (2–3): 91—114. doi:10.1007/s10601-006-8058-9..
- ↑ Elkies, Noam D. (1998). The still life density problem and its generalizations. Voronoi's Impact on Modern Science, Book I. Proc. Inst. Math. Nat. Acad. Sci. Ukraine, vol. 21. с. 228—253. arXiv:math.CO/9905194.
- ↑ J. Larrosa, E. Morancho and D. Niso (2005). On the Practical use of Variable Elimination in Constraint Optimization Problems: 'Still-life' as a Case Study. Journal of Artificial Intelligence Research. 23: 421—440. Архів оригіналу за 16 липня 2011.
- ↑ Neil Yorke-Smith. Maximum Density Still Life. Artificial Intelligence Center. SRI International.
- ↑ Number of stable n-celled patterns («still lifes») in Conway's game of Life
- ↑ Number of n-celled pseudo-still-lifes in Conway's game of Life
- ↑ Niemiec, Mark D. Life Still-Lifes. Архів оригіналу за 21 січня 2013. Процитовано 4 серпня 2017.