Вузол
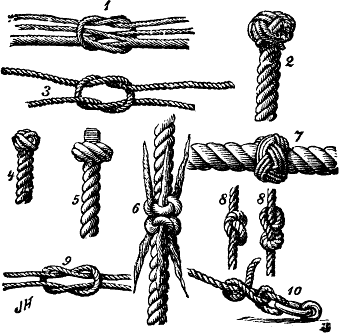
1. Сплетення
2. Вузол Манропа
3. Бабин вузол
4. Контрольний вузол «трояндовий бутон»(?)
5. Вузол Меттью Вокера
6. Вантовий кноп
7. Турецька голова
8. Простий вузол, вісімка
9. Прямий вузол
10. Простий штик
Ву́зол — спосіб кріплення або закріплення лінійних гнучких матеріалів, як-от мотузок, сполученням або переплетенням. Він може складатися з довжини одного або декількох сегментів мотузки, нитки, лямки, шпагату, ремінця або навіть ланцюга, переплетеного таким чином, що лінія може зв'язуватися з собою чи з іншим об'єктом.
Вузли цікаві своїм давнім походженням, своїм практичним застосуванням, а також теорією вузлів — галуззю математики, яка досліджує їхні властивості. Існує велика різноманітність вузлів, кожен з яких має властивості, що робить його придатним для виконання низки завдань. Деякі вузли використовуються для прикріплення мотузки (або іншого з'єднувального матеріалу) до інших предметів, як-от інших мотузок, кільця або кола. Деякі вузли використовуються для зв'язування або стиснення об'єктів. Декоративні вузли зазвичай прив'язуються для виготовлення привабливих візерунків.
Вивчення[ред. | ред. код]
Хоча деякі люди можуть дивитися на діаграми чи фотографії та зв'язати ілюстровані вузли, інші вивчають вузли досконаліше, спостерігаючи за тим, як вузол пов'язаний. Методи зв'язки вузлів часто передаються матросами, скаутами, альпіністами, спелеологами, арбористами, рятувальними фахівцями, етапними гравцями, рибаками, льотчиками та хірургами. Міжнародна гільдія Knot Tyers є організацією, що займається заохоченням зв'язування вузлів.
Використання[ред. | ред. код]
У небезпечних середовищах, як-от гори, вузли дуже важливі. У разі того, як хтось потрапляє в яр або подібну місцевість, з правильним обладнанням та знаннями вузлів можна встановити систему Раппеля, щоб опустити рятівника до аварії та встановити систему тягової маніпуляції, щоб третя особа витягнула і рятувальника, і потерпілого з яру. Подальше застосування вузлів включає в себе розробку високої лінії, яка аналогічна лінії блискавки, і яка може використовуватися для переміщення запасів, поранених людей через річки, щілини або яри. Зверніть увагу, що згадані системи зазвичай вимагають карабінів та використання декількох відповідних вузлів. До цих вузлів належать дубль, подвійна фігура вісім, мисливський гак, мантер мул, прусик, автоблокування і гвоздика. Таким чином, будь-яка особа, яка перебуває в гірській місцевості, повинна мати базові знання про вузли, щоб підвищити власну безпеку.

Вузли можна застосовувати в комбінації для створення складних об'єктів, як-от ремінець та сітка. У мотузці, потертий кінець каната тримається разом за типом вузла, який називається збитим вузлом. Багато видів текстилю використовують вузли для ремонту пошкоджень. Макраме, один з видів текстилю, виробляється виключно за допомогою вузлів, а не в'язання гачком, плетіння або валяння. Способом макраме можна виготовляти самостійні тривимірні текстильні конструкції, а також плоскі роботи, і які часто використовуються оздоблення або декорації.
Див. також[ред. | ред. код]
Посилання[ред. | ред. код]
- Базові вузли для застосування у туризмі [Архівовано 13 липня 2012 у Wayback Machine.]
- Вузол [Архівовано 14 червня 2021 у Wayback Machine.] // Українська мала енциклопедія : 16 кн. : у 8 т. / проф. Є. Онацький. — Накладом Адміністратури УАПЦ в Аргентині. — Буенос-Айрес, 1958. — Т. 1, кн. II : Літери В — Ґ. — С. 216-217. — 1000 екз.
- Animated knots (англ.)
- Instructions for tying knots [Архівовано 16 грудня 2017 у Wayback Machine.] (англ.)
- Web directory of knots [Архівовано 22 квітня 2009 у Wayback Machine.] (англ.)
|