Теорія вузлів


В топології, теорія вузлів вивчає математичні вузли. На відміну від вузлів, які зустрічаються в повсякденному житті, такі як, наприклад, вузли на шнурках, математичні вузли завжди замкнені, тобто, їхні кінці не можуть бути роз'єднані. Мовою математики, вузол — це вкладення кола в тривимірний евклідів простір, R3 (у топології, коли ми говоримо про коло, то не обмежуємося його звичним геометричним змістом, але включаємо в це поняття всі його гомеоморфізми). Два математичні вузли вважаються однаковими, якщо їх можна перевести один в інший деформацією простору R3 всередині самого себе (відома як охоплювальна ізотопія); до цих трансформацій відносяться такі маніпуляції з вузлом, що не включають його розрізання і подальше склеювання, або проходження кривої, що формує вузол, самої через себе.
Вузли можна описати різними способами. Наприклад, поширеним методом описання вузла є пласка схема, що називається діаграмою вузла. Але будь-який вузол можна зобразити на ній багатьма різними способами. З цього випливає одна з фундаментальних проблем теорії вузлів — визначити, чи зображують два різні описи один і той самий вузол.
Розв'язки цієї задачі існують, але їхня складність невідома. На практиці, вузли часто порівнюють, використовуючи інваріанти — кількісні характеристики вузлів, що є незмінними для вузла незалежно від способу його зображення. Важливими інваріантами є різноманітні многочлени вузлів, група вузла, а також гіперболічні інваріанти.
Початковою задачею теорії вузлів було створення таблиці вузлів і зачеплень (вузли з кількох компонент, переплетених між собою). З тих пір було описано близько шести мільярдів вузлів і зачеплень.[джерело?]
Для подальшого розширення теорії вузлів вони генералізуються в кількох напрямках. Вузли можуть вкладатися в інші, неевклідові простори, і вкладатися можуть не кола, а інші об'єкти. Вузлами високих вимірів називають n-вимірні сфери, що вкладені у m-вимірні евклідові простори.
Історія[ред. | ред. код]

За даними археології, вузли почали в'язати ще в доісторичні часи. Окрім практичного використання, такого як зв'язування предметів або запис інформації, вузли цікавили людей як естетичні об'єкти та релігійні символи. Вузли часто використовуються в китайських витворах мистецтва, що зустрічаються починаючи з кількох століть до нашої ери. Нескінченний вузол трапляється в тибетському буддизмі, тоді як кільця Борромео зустрічаються в різноманітних археологічних згадках різних культур. Кельтські монахи, що створили Келлську книгу, вкривали цілі сторінки заплутаними кельтськими вузлами.
Математичну теорію вузлів започаткував Александр-Теофіл Вандермонд, який довів важливість топологічних ознак для властивостей вузлів. Дослідження вузлів почав у XIX столітті, Гаус, який ввів поняття коефіцієнта зачеплення. В 1860-х теорія лорда Кельвіна про те, що атоми є вузлами в ефірі, спонукала Пітера Гатрі Тета створити першу класифікацію вузлів. Тет опублікував 1885 року таблицю вузлів які мають до 10 зачеплень. Це дослідження мотивувало ранніх дослідників вузлів, але несподівано теорія вузлів стала частиною динамічної дисципліни топології. [1]

Еквівалентність вузлів[ред. | ред. код]
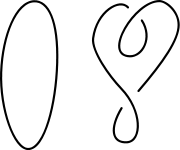
|

| |
Зліва - тривіальний вузол, і вузол, еквівалентний йому. Але для більш складних вузлів, таких як вузол справа, може бути складніше встановити їхню еквівалентність тривіальному.
| ||
Вузол будується, починаючи з одновимірного сегменту, який подовжується, і, можливо, обертається кілька разів навколо самого себе, а потім поєднується зі своїм власним початком. Можна сказати, що вузол це ін'єктивна і неперервна функція і . Топологи зауважують, що вузли й інші подібні об'єкти, такі як зачеплення і коси є еквівалентними, якщо їх можна перевести один в одного без розривів і самоперетинів. Формально це можна сформулювати так: два вузли є еквівалентними, якщо існує гомеоморфізм зі збереженою орієнтацією , такий, що
Базова проблема теорії вузлів — проблема розпізнавання, доведення еквівалентності двох вузлів. Алгоритми для вирішення цієї проблеми створив Вольфганг Гакен[en] у 1960-х. Але ці алгоритми дуже часоємні. Частковим випадком цієї проблеми є відрізнення тривіального вузла від нетривіального (unknotting problem).
Діаграма вузла[ред. | ред. код]
Зручний спосіб візуалізувати й маніпулювати вузлом полягає в тому, щоб спроєктувати вузол на площину, і позначити в точках перетину ліній, яка з них проходить над іншою — таким чином, проєкція буде ін'єктивним відображенням вузла. Зазвичай у цих точках лінія, що йде знизу, розривається.[2]
Такі діаграми називають діаграмами вузлів, або діаграмами зачеплень (залежно від того, що вони репрезентують).
Аналогічно, заплутані поверхні в 4-вимірному просторі можна спроєктувати на 3-вимірний простір.
Спрощеною діаграмою вузла називається така діаграма, в якій нема перетинів, що можуть бути прибраними.
Рухи Рейдемейстера[ред. | ред. код]
1927 року, працюючи з діаграмами вузлів, Джеймс Александер[ru] і Г. Б. Бріггс, і, незалежно від них, Курт Рейдемейстер, показали, що дві діаграми, які належать одному вузлу, можна перетворити одну в іншу послідовністю операцій певного виду[3]. Такі операції називають зараз рухами Рейдемейстера, і їх є три види:
- перекрутити лінію,
- накласти одну лінію на іншу,
- перенести лінію через точку перетину інших ліній.
 |

|
| Тип I | Тип II |

| |
| Тип III | |
Інваріанти вузлів[ред. | ред. код]
Інваріантами вузла називаються величини, що є однаковими для будь-яких еквівалентних вузлів. Якщо два вузли мають різні значення інваріантів, то ці вузли нееквівалентні. Проте, в загальному випадку, рівність інваріантів не доводить еквівалентності вузлів, бо різні вузли можуть мати деякі з інваріантів однаковими.
«Класичні» інваріанти вузлів включають фундаментальну групу доповнення до вузла і многочлен Александера. В кінці XX століття відкрито такі інваріанти як квантові многочлени, інваріанти Васильєва і гіперболічні інваріанти.
Многочлени вузлів[ред. | ред. код]
Многочленом вузла називають інваріант вузла у формі многочлена, коефіцієнти якого кодують деякі властивості цього вузла.
Перший многочлен вузла, многочлен Александера, відкрив Джеймс Александер 1923 року, але інші многочлени відкрито лише через 60 років.
У 1960-х, Джон Конвей запропонував скейн-співвідношення для нової версії многочлена Александера, яка називається тепер многочленом Александера — Конвея. Важливість скейн-співвідношень не була зрозумілою до 1980-х, коли Воен Джонс відкрив многочлен Джонса. Це підштовхнуло до відкриття багатьох інших многочленів, таких як многочлен HOMFLY
Невдовзі після відкриття Джонса, Луїс Кауфман помітив, що многочлен Джонса можна обчислити в термінах моделі сум і станів, і вивів таким чином дужку Кауфмана, інваріант для обрамленого вузла. Це відкриття показало глибокий зв'язок між теорією вузлів і статистичною механікою.
Кожній діаграмі неорієнтованого зачеплення зіставляється дужка Кауфмана від змінних таким чином, щоб виконувалися співвідношення:

Маленькі картинки у першому співвідношенні позначають діаграми, які збігаються поза пунктирними колами, а всередині влаштовані так, як показано на картинках. Якщо позначити діаграми відповідно

то перше співвідношення можна записати як Для перехрестя діаграми уміщеного в коло, діаграми визначені однозначно, незалежно від того, як воно повернуте. Дуги діаграм обираються в областях та відповідно. Позначмо літерою чверть кола, яка при вході у коло є видною ліворуч, і ту чверть кола, яка при виході з кола видна праворуч. Це визначення не залежить від того, з якого боку зайти до кола.

Співвідношення 2 означає, що додавання до діаграми кола, яке не перетинає проєкції відповідного діаграмі зачеплення, приводить до многочлена, який отримується з початкового множенням на Співвідношення 3 означає, що колу відповідає многочлен, який дорівнює 1. Многочлен не змінюється за плоскої ізотопії діаграми. Використавши багаторазово співвідношення 1 і один раз використавши співвідношення 2, отримаємо

Таким чином вдається пов'язати змінні співвідношеннями, щоб отриманий многочлен був інваріантним відносно рухів Рейдемейстра[4].
Приклади многочленів для деяких вузлів:
| Форма Александера — Бріґґза | Многочлен Александера | Многочлен Конвея | Многочлен Джонса | Многочлен HOMFLY |
|---|---|---|---|---|
| (Тривіальний вузол)[5] | ||||
| (Трилисник)[6] | ||||
| (Вісімка)[7] | ||||
| (Перстач)[8] | ||||
| (Бабин вузол)[9] | ||||
| (Прямий вузол)[10] | |
Скейн-співвідношення[ред. | ред. код]
Скейн-співвідношеннями називається рекурсивний спосіб обчислення многочленів. Вони задають співвідношення між трьома діаграмами вузлів, що відрізняються лише в одній точці — в одній з них лінії не перетинаються, у двох інших одна чи інша лінія знаходиться згори. Їх позначають як таким чином:

Кінцевий результат обчислень не залежить від того, як саме ми будемо рухатись по вузлу, але важливо весь час дотримуватися одного й того ж напрямку.
Багато многочленів вузлів можна задати тим чи іншим скейн-співвідношенням. Наприклад, многочлен Джонса задається таким чином:
А многочлен Конвея, так:
(В обох випадках, значення многочлена для тривіального вузла дорівнює одиниці).
Послідовно виражаючи діаграму через простіші, будь-який вузол можна звести до тривіального.[11]
Застосування теорії вузлів[ред. | ред. код]
Деякі автори вважають, що є тісний зв'язок між квантовою теорією і теорією вузлів. Наприклад, рівняння Янга — Бакстера[ru], що використовуються в квантовій механіці і статистичній механіці, є еквівалентними третьому руху Рейдемейстера, а модель Поттса, що описує фазові переходи речовини, має математичні зв'язки з многочленом Джонса.
Інваріанти Васильєва можна використати для побудови біалгебра[en], схожих на алгебри діаграм Фейнмана.
Ці зв'язки використовуються для топологічного описання квантової теорії.[1]
Примітки[ред. | ред. код]
- ↑ а б Узлы. ХРОНОЛОГИЯ ОДНОЙ МАТЕМАТИЧЕСКОЙ ТЕОРИИ (PDF). Архів оригіналу (PDF) за 13 грудня 2016. Процитовано 22 серпня 2016.
- ↑ Узлы и их инварианты (PDF). Архів оригіналу (PDF) за 7 червня 2013. Процитовано 22 серпня 2016.
- ↑ Экскурс в теорию узлов (PDF). Архів оригіналу (PDF) за 29 березня 2017. Процитовано 22 серпня 2016.
- ↑ В.В.Прасолов, А.Б.Сосинский - Узлы, зацепления, косы и трехмерные многообразия.
- ↑ Тривіальний вузол в Атласі вузлів. Архів оригіналу за 16 серпня 2016. Процитовано 22 серпня 2016.
- ↑ Трилисник в Атласі вузлів. Архів оригіналу за 12 серпня 2016. Процитовано 22 серпня 2016.
- ↑ Вісімка в Атласі вузлів. Архів оригіналу за 13 серпня 2016. Процитовано 22 серпня 2016.
- ↑ П'ятилисник (перстач) в Атласі вузлів. Архів оригіналу за 26 серпня 2016. Процитовано 22 серпня 2016.
- ↑ Бабин вузол. Архів оригіналу за 23 серпня 2016. Процитовано 22 серпня 2016.
- ↑ Прямий вузол. Архів оригіналу за 25 серпня 2016. Процитовано 22 серпня 2016.
- ↑ Математика XX века. Архів оригіналу за 28 серпня 2016. Процитовано 22 серпня 2016.
Посилання[ред. | ред. код]
Таблиці вузлів і програмне забезпечення для вивчення вузлів[ред. | ред. код]
- KnotInfo [Архівовано 9 грудня 2019 у Wayback Machine.] — таблиці інваріантів вузлів та ресурси теорії вузлів (база даних)
- The Knot Atlas [Архівовано 28 червня 2021 у Wayback Machine.] — детальна інформація про вузли, подана у таблицях (вікі)
- KnotPlot [Архівовано 10 травня 2020 у Wayback Machine.] — програмне забезпечення для вивчення геометричних властивостей вузлів
- Knotscape [Архівовано 28 лютого 2020 у Wayback Machine.] — програмне забезпечення для створення зображень вузлів
- Knoutilus [Архівовано 27 червня 2020 у Wayback Machine.] — онлайн база даних та генератор зображень вузлів
- KnotData.html [Архівовано 18 вересня 2020 у Wayback Machine.] — функції Wolfram Mathematica для дослідження вузлів
|
| ||||||||||||||||||||||||||||

![{\displaystyle K\colon [0,1]\to \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3527c328346ff511b17bd2fe2ae5f3504df3d2e9)














































