Нарисна геометрія
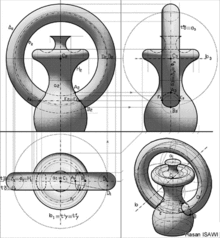
Нарисна́ геоме́трія[1][2] (описо́ва геоме́трія), заст. начерта́льна геометрія[3] — це розділ геометрії, що вивчає методи зображення тривимірних об'єктів (оригіналів), використовуючи двовимірні проєкції (зображення).
Історична довідка[ред. | ред. код]
Перші спроби встановлення правил побудови зображень були ще у 3 — 4 ст. до н. е. Так, римський архітектор Вітрувій у своєму трактаті «Десять книг про архітектуру» (1 ст. до н. е.) дає поняття про план (горизонтальну проєкцію) і фасад (фронтальну проєкцію) споруди. Італійський архітектор і вчений Л. Альберті (15 ст. н. е.) у трактаті «На картині» (лат. De pictura, 1435) уже застосовує поняття «зникома точка» й дає важливий для практики спосіб побудови перспективи за допомогою сітки. У «Трактаті про живопис» (1651) Леонардо да Вінчі дано численні вказівки щодо практичного застосування перспективних зображень, зокрема про «спостережну» перспективу. Німецький художник А. Дюрер у праці «Керівництво до вимірювання циркулем і лінійкою…» (нім. Underweysung der messung mit dem zirckel und richtscheyt in Linien ebnen vnnd gantzen corporen durch Albrecht Dürer zusamen getzogen und zu nutz allen kunstlieb habenden mit zugehörigen figuren in truck gebracht im jar. MDXXV, 1525) запропонував спосіб побудови перспективи за горизонтальною і фронтальною проєкціями об'єкта. Найповніший виклад прийомів побудови перспективи був зроблений італійським вченим Гвідобальдо дель Монте у творі «Теорія перспективи» (лат. Perspectivae libri sex, 1600).
Основи нарисної геометрії як науки заклав французький інженер Гаспар Монж. Г. Монж розробив свою методику в 1765, працюючи креслярем при спорудженні фортифікацій.
У ході подальшого розвитку нарисна геометрія розширила свої можливості за рахунок застосування проеціювання в'язками і пучками площин, прямими лінійних конгруенцій, конгруенціями кривих ліній, проеціювання багатовимірного простору на простір тієї ж чи меншої розмірності, використання ідей проєктивної геометрії, геометричного моделювання тощо.
Відображення у нарисній геометрії[ред. | ред. код]
Основним способом відображення у нарисній геометрії є проєціювання; одержане при цьому зображення називається проєкцією. Щоб повніше відобразити геометричні властивості фігури-оригіналу, її положення в просторі та залежно від вимог до зображення користуються різними методами проеціювання, внаслідок чого утворюються різні типи проєкцій, найпоширенішими з яких є паралельні та центральні проєкції.
Види проєкцій[ред. | ред. код]
Паралельні проєкції[ред. | ред. код]
До паралельних проєкцій належать ортогональні, аксонометричні та проєкції з числовими відмітками.
Ортогональні проєкції — прямокутні проєкції на дві (чи більше) взаємно перпендикулярні площини проєкцій (метод Монжа). Одну площину проєкцій розташовують горизонтально, другу — вертикально. Кожну точку фігури-оригіналу проєктують прямокутно на ці площини. Побудовані проєкції обертанням площин проєкцій суміщують в одну площину. Одержане комплексне креслення складається з двох взаємно пов'язаних проєкцій.
Найпоширенішими видами аксонометричних проєкцій є прямокутна ізометрія, прямокутна диметрія і косокутна фронтальна диметрія, що розрізняються розташуванням координатних осей та коефіцієнтами спотворення (відношеннями зображення відрізка прямої, паралельної відповідній координатній осі, до його натурального розміру). У прямокутній ізометрії осі координат утворюють між собою рівні кути, а коефіцієнти спотворення рівні між собою. В прямокутній диметрії вісь OZ вертикальна, осі OX та OY утворюють з горизонтальним напрямом кути 7°10' та 41°25' відповідно, коефіцієнти спотворення по осях OX та OZ рівні між собою, а по осі OY цей коефіцієнт удвічі менший. У косокутній фронтальній диметрії осі OZ та OX перпендикулярні, вісь OY утворює з ними кут 135°, відрізки, паралельні до осей OX та OZ, не спотворюються, а паралельні до осі OY зменшуються вдвоє. Якщо всі три коефіцієнти різні, то одержуємо триметрію.
Проєкції з числовими відмітками — прямокутні проєкції точок на горизонтальну площину, що супроводяться числами, які вказують віддалі точок-оригіналів від цієї площини. Застосовуються в геодезії, топографії, будівництві, гірничій справі, геології тощо.
Центральні проєкції[ред. | ред. код]
Центральні проєкції є геометричною основою перспективи.
Проєкції у нарисній геометрії[ред. | ред. код]
Нарисна геометрія використовує ортогональні та аксонометричні проєкції.
Зазвичай використовуються
- Фронтальна проєкція або вид спереду
- Горизонтальна проєкція або вид зверху
- Бічна проєкція, або вид зліва.
Видимі контури предметів зображаються суцільними лініями, невидимі — штриховими.
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Нарисний // Великий тлумачний словник сучасної української мови (з дод. і допов.) / уклад. і гол. ред. В. Т. Бусел. — 5-те вид. — К. ; Ірпінь : Перун, 2005. — ISBN 966-569-013-2.
- ↑ Нарисна // Словник української мови : в 11 т. — Київ : Наукова думка, 1970—1980.
- ↑ Начертальна // Словник української мови : в 11 т. — Київ : Наукова думка, 1970—1980.
Джерела[ред. | ред. код]
- Павленко І. В. Нарисна геометрія [Архівовано 12 червня 2015 у Wayback Machine.] / І. В. Павленко, В. В. Павленко. — Суми: СумДУ, 2015. — 239 с.
- Гордон В. О. Семенов-Огиевский М. А. Курс начертательной геометрии. — М.: Наука, 1988. — 272 с.
- Потишко А. В., Крушевская Д. П. Справочник по инженерной графике. 2-е изд., перераб. и доп. / Под ред. А. В. Потишко. — К.: Будівельник, 1983. — 264 с.
Посилання[ред. | ред. код]
| Вікісховище має мультимедійні дані за темою: Нарисна геометрія |
- Нарисна геометрія // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 131. — ISBN 978-966-7407-83-4.
- «Нарисна геометрія» [Архівовано 22 травня 2017 у Wayback Machine.] / Українська радянська енциклопедія : у 12 т. / гол. ред. М. П. Бажан ; редкол.: О. К. Антонов та ін. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985.
|