Полігональна сітка

Полігональна сітка (англ. Polygon mesh) — це набір вершин, ребер, та граней, що описують форму багатогранного об'єкта в тривимірній графіці та твердотілому моделюванні. Грані зазвичай складаються з трикутників (сітка з трикутників), чотирикутників, чи інших опуклих многокутників, що спрощує їх рендеринг, хоча можуть використовуватись і загальніші, неопуклі многокутники, чи багатокутники з дірками.
Дослідження полігональних сіток — це великий підрозділ комп'ютерної графіки та геометричного моделювання. Різні представлення полігональних сіток використовуються для різних цілей та застосунків. Серед операцій, які можна виконувати над сітками, можуть бути операції булевої алгебри, згладжування, спрощення та багато інших. Для передачі полігональних сіток по мережі використовуються мережеві представлення, такі як «потокові» та «прогресивні» сітки. Об'ємні сітки відрізняються від полігональних тим, що вони явно представляють поверхню та об'ємні структури, тоді як полігональні сітки явно представляють лише поверхню, а об'єм залишається неявним. Оскільки полігональні сітки широко використовуються в комп'ютерній графіці, для них розроблені алгоритми трасування променів, виявлення зіткнень та динаміки твердих тіл[en].
Математичний еквівалент полігональних сіток — неструктуровані сітки. Вони досліджуються методами дискретної геометрії.
Елементи моделювання сітки[ред. | ред. код]
Об'єкти, створені за допомогою полігональних сіток, повинні зберігати різні типи елементів, такі як вершини, ребра, грані, многокутники (полігони) та поверхні. У багатьох випадках, зберігаються лише вершини, ребра, грані, або многокутники. Деякі візуалізатори можуть підтримувати лише тристоронні грані, тому полігони повинні бути побудовані із них, як показано вище. Однак, багато візуалізаторів підтримують многокутники з чотирма та більше сторонами, або вміють перетворювати многокутники в трикутники, роблячи необов'язковим зберігання сітки в тріангульованому вигляді. Також в деяких випадках, таких як моделювання голови, бажано вміти створювати тристоронні і чотиристоронні многокутники.
Вершина: містить інформацію, таку як позиція (зазвичай у тривимірному просторі), колір, нормальний вектор та координати текстури.
Ребро з'єднує дві вершини.
Грань це набір ребер, в якому трикутна грань має три ребра та чотирикутна — чотири. Багатокутник (Полігон) містить довільну кількість граней. У системах, які підтримують багатосторонні грані, полігони та грані еквівалентні. Однак, більшість апаратного забезпечення для рендерингу підтримує лише грані з трьома або чотирма сторонами, так що полігони представлені як множина граней. Математично, полігональна сітка може бути представлена у вигляді неструктурованої сітки, або неорієнтованого графа, з додаванням властивостей геометрії, форми та топології.
Поверхні, або групи згладжування, корисні, але не обов'язкові для групування гладких областей. Розглянемо циліндр із кришкою, такий як пляшка з газованою водою. Для плавного затінення боків всі нормалі поверхні повинні бути спрямовані горизонтально від центру, тоді як нормалі шапок повинні бути спрямовані прямо вгору і вниз. Видані у вигляді єдиної поверхні, затіненої за Фонгом, вершини складки мали б неправильні нормалі. Таким чином, для групування гладких частин сітки необхідний певний спосіб визначення місця припинення згладжування, подібно до того, як багатокутники групують 3-сторонні грані. Як альтернатива забезпеченню поверхонь / згладжувальних груп, сітка може містити інші дані для обчислення тих самих даних, наприклад, кут розщеплення (полігони з нормалями вище цього порогу або автоматично обробляються, як окремі згладжувальні групи, або деякі методи, такі як розщеплення або фаска автоматично застосовується до краю між ними). Крім того, сітки з дуже високою роздільною здатністю менш схильні до проблем, які потребують згладжування груп, оскільки їх багатокутники настільки малі, що робить потребу неактуальною. Крім того, існує ще одна альтернатива у можливості простого від'єднання самих поверхонь від решти сітки. Візуалізатори не намагаються згладжувати краї несуміжних багатокутників.
Групи: Деякі формати сіток містять групи, які визначають окремі елементи сітки, і корисні для визначення окремих під-об'єктів для скелетної анімації, або окремих виконавців для нескелетної анімації.
Матеріали: Як правило, визначаються матеріали, що дозволяють різним частинам сітки використовувати різні шейдери при отриманні.
Більшість форматів сіток також підтримують певну форму УФ-координат, які є окремим двовимірним поданням сітки, "розгорнутою", щоб показати, яку частину двовимірної карти текстури застосовувати до різних полігонів сітки. Також сітки можуть містити іншу інформацію про такі атрибути вершин, як колір, дотичні вектори, карти ваги для управління анімацією тощо (іноді їх також називають каналами).
Представлення[ред. | ред. код]

Полігональні сітки можуть бути представлені безліччю способів, використовуючи різні способи зберігання вершин, ребер і граней. У них входять:
- Список граней: опис граней відбувається за допомогою покажчиків в список вершин.
- «Крилате» представлення: у ньому кожна точка ребра вказує на дві вершини, дві грані і чотири (за годинниковою стрілкою і проти годинникової) ребра, яким вона належить. Крилате подання дозволяє обійти поверхню за сталий час, але у нього великі вимоги по пам'яті для зберігання даних опису сітки.
- Півреберні сітки: спосіб схожий на «крилате» представлення, за винятком того, що використовується інформація обходу лише половини грані.
- Чотириреберні сітки, які зберігають ребра, півребра і вершини без будь-якої вказівки на полігони. Полігони прямо не виражені в представленні, і можуть бути обчислені при обході структури. Вимоги по пам'яті аналогічні півреберним сіткам.
- Таблиця кутів, які зберігають вершини в зумовленій таблиці, такій, що обхід таблиці неявно задає полігони. По суті, це «віяло трикутників», використовуване в апаратному рендерінгу. Представлення більш компактне і більш продуктивне для знаходження полігонів, але операції по їх зміні повільні. Більш того, таблиці кутів не подають сітки повністю. Для представлення більшості сіток потрібно кілька таблиць кутів (віял трикутників).
- Вершинне представлення: представлені лише вершини, що вказують на інші вершини. Інформація про грані та ребра виражена неявно в цьому поданні. Однак, простота представлення дозволяє проводити над сіткою безліч ефективних операцій.
Кожне з представлень має свої переваги і недоліки.
Вибір структури даних визначається застосуванням, необхідною продуктивністю, розміром даних, операціями, які будуть виконуватися. Наприклад, легше мати справу з трикутниками, ніж з багатокутниками загального вигляду, особливо в обчислювальній геометрії. Для певних операцій необхідно мати швидкий доступ до топологічної інформації, такої як ребра або сусідні грані; для цього потрібні більш складні структури, такі як «крилате» представлення. Для апаратного рендерінгу потрібні компактні, прості структури; тому в API низького рівня, такі як DirectX і OpenGL зазвичай включена таблиця кутів (віяло трикутників).
Вершинне представлення[ред. | ред. код]
Вершинне представлення описує об'єкт як множину вершин, з'єднаних з іншими вершинами. Це найпростіше представлення, але воно не широко використовується, тому що інформація про грані та ребра не виражена явно. Тому потрібно обійти всі дані, щоб згенерувати список граней для візуалізації. Крім того, нелегко виконуються операції на ребрах і гранях. Однак, сітки ВП отримують вигоду з малого використання пам'яті і ефективної трансформації.
Список граней[ред. | ред. код]

Сітка з використанням списку граней представляє об'єкт як множину граней і множину вершин. Це саме найпоширеніше представлення, будучи вхідними даними типово прийнятими сучасним графічним обладнанням.
Список граней кращий для моделювання, ніж вершинне представлення тим, що він дозволяє явний пошук вершин грані, і граней оточуючих вершину. Для рендерінгу грань звичайно посилається в графічний процесор як безліч індексів вершин, і вершини надсилаються як позиція / колір / структури нормалей. Тому зміни форми, але не геометрії, можуть бути динамічно оновлені простим пересиланням даних вершини без оновлення зв'язності граней.
Моделювання вимагає легкого обходу всіх структур. З сіткою, що використовує список граней дуже легко знайти вершини грані. Також, список вершин містить список всіх граней пов'язаних з кожною вершиною. На відміну від вершинного представлення, і грані і вершини явно представлені, так що знаходження сусідніх граней і вершин постійно за часом. Однак, ребра не задані явно, так що пошук все ще потрібен, щоб знайти всі грані, які є навколо заданої грані. Інші динамічні операції, такі як розрив або об'єднання граней, також є складними операціями зі списком граней.
Кожне з наведених представлень з порівнянням переваг та недоліків, дискутується у статті Сміта (2006).[1]
«Крилате» представлення[ред. | ред. код]
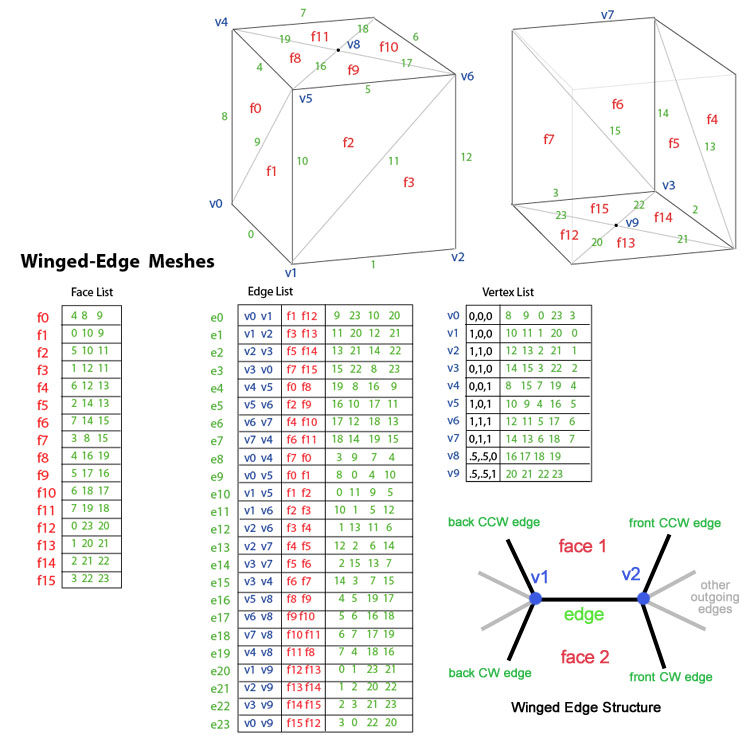
Представлене Брюсом Баумгартеном 1975 року, «Крилате» представлення явно представляє вершини, грані і ребра сітки. Це представлення широко використовується в програмах для моделювання для надання найвищої гнучкості в динамічній зміні геометрії сітки, тому що можуть бути швидко виконані операції розриву та об'єднання. Їх основний недолік — високі вимоги до пам'яті і збільшена складність через вміст великої кількості індексів.
«Крилате» представлення вирішує проблему обходу від ребра до ребра і забезпечує упорядковану множину граней навколо ребра. Для будь-якого заданого ребра число вихідних ребер може бути довільним. Щоб спростити це, «крилате» представлення надає лише чотири, найближчих ребра за годинниковою і проти годинникової стрілки на кожному кінці ребра. Інші ребра можна обійти поступово. Тому інформація про кожне ребро нагадує метелика, завдяки чому подання називається «крилатим».
Візуалізація «крилатого» представлення графічним обладнанням вимагає генерування списку індексів граней. Зазвичай це робиться тільки тоді, коли змінюється геометрія поверхні. «Крилате» представлення ідеально підходить для динамічної геометрії, таких задач як розбиття поверхонь і інтерактивне моделювання, тому що зміни сітки можуть відбуватися локально. Перетин вздовж сітки, який може знадобитись при виявлення зіткнень, може бути виконаним ефективно.
Подробиці можна знайти в статті Баумгарта (1975).[2]
Короткий зміст представлення сітки[ред. | ред. код]
| Операція | Вершина-вершина | Грань-вершина | Крилатий край | Динамічна візуалізація | |
|---|---|---|---|---|---|
| V-V | Всі вершини навколо вершини | Явний | V → f1, f2, f3, ... → v1, v2, v3,. . . | V → e1, e2, e3, ... → v1, v2, v3,. . . | V → e1, e2, e3, ... → v1, v2, v3,. . . |
| E-F | Всі ребра грані | F (a, b, c) → {a, b}, {b, c}, {a, c} | F → {a, b}, {b, c}, {a, c} | Явний | Явний |
| V-F | Всі вершини грані | F (a, b, c) → {a, b, c} | Явний | F → e1, e2, e3 → a, b, c | Явний |
| F-V | Всі грані навколо вершини | Пошук пар | Явний | V → e1, e2, e3 → f1, f2, f3,. . . | Явний |
| E-V | Всі ребра навколо вершини | V → {v, v1}, {v, v2}, {v, v3},. . . | V → f1, f2, f3, ... → v1, v2, v3,. . . | Явний | Явний |
| F-E | Обидві грані ребра | Список порівняння | Список порівняння | Явний | Явний |
| V-E | Обидві вершини ребра | E (a, b) → {a, b} | E (a, b) → {a, b} | Явний | Явний |
| потік | Знайдіть грані із заданими вершинами | F (a, b, c) → {a, b, c} | Встановити перетин v1, v2, v3 | Встановити перетин v1, v2, v3 | Встановити перетин v1, v2, v3 |
| Розмір зберігання | V * avg (V, V) | 3F + V * avg (F, V) | 3F + 8E + V * avg (E, V) | 6F + 4E + V * avg (E, V) | |
| Приклад з 10 вершинами, 16 гранями, 24 ребрами: | |||||
| 10 * 5 = 50 | 3 * 16 + 10 * 5 = 98 | 3 * 16 + 8 * 24 + 10 * 5 = 290 | 6 * 16 + 4 * 24 + 10 * 5 = 242 | ||
| Малюнок 6: короткий зміст операцій представлення сітки | |||||
У наведеній вище таблиці "явне" вказує на те, що операцію можна виконувати за сталий час, оскільки дані зберігаються безпосередньо; "список порівняння" вказує на те, що для виконання операції необхідно виконати порівняння списків; а "пошук пар" вказує, що пошук потрібно проводити за двома індексами. Позначення "avg (V, V)" означає середню кількість вершин, підключених до даної вершини; "avg (E, V)" означає середню кількість ребер, підключених до даної вершини, а "avg (F, V)" - середня кількість граней, підключених до даної вершини.
Позначення "V → f1, f2, f3, ... → v1, v2, v3, ..." описує, що для виконання операції необхідний обхід декількох елементів. Наприклад, щоб отримати "всі вершини навколо даної вершини V", використовуючи сітку грань-вершина, необхідно спочатку знайти грані навколо даної вершини V, використовуючи список вершин. Потім за цими гранями використовуйте список граней, щоб знайти вершини навколо них. Зверніть увагу, що крилаті сітки явно зберігають майже всю інформацію, а інші операції завжди переходять спочатку до ребра, щоб отримати додаткову інформацію. Сітки вершин-вершин є єдиним виображенням, яке явно зберігає сусідні вершини даної вершини.
У міру того, як уявлення сітки стають більш складними (зліва направо в представленні сітки), кількість явно збереженої інформації збільшується. Це дає більше абсолютного, сталого часу, доступу до обходу та топології різних елементів, але ціною збільшення накладних витрат та простору для належного ведення індексів.
На малюнку 7 показана інформація про зв’язок для кожного з чотирьох методів, описаних у цій статті. Також існують інші уявлення, такі як напівребра та кутові таблиці. Це всі варіанти того, як вершини, грані та ребра індексують один одного.
Як загальне правило, грані-вершини сітки використовуються всякий раз, коли об'єкт повинен бути відтворений на графічному обладнанні, яке не змінює геометрію (зв'язок), але може деформувати або змінити форму (положення вершин), наприклад, візуалізація в реальному часі статичних або морфінгуючих об'єктів. Візуалізація динамічної сітки або крилате ребро використовуються при зміні геометрії, наприклад, в інтерактивних пакетах моделювання або для обчислення поверхових підрозділів. Вершинно-вершинні сітки ідеально підходять для ефективних, складних змін геометрії або топології, якщо апаратне відображення не викликає занепокоєння.
Формати файлів[ред. | ред. код]
Існує безліч різних форматів файлів для зберігання даних полігональних сіток. Кожен формат є найефективнішим, якщо використовується для цілей, призначених його творцем. Деякі з цих форматів представлені нижче:
| Суфікс файлу | Назва формату | Організація (ї) | Програма (и) | Опис |
|---|---|---|---|---|
| .raw | Raw mesh | Unknown | Various | Відкритий формат, призначений лише для ASCII. Кожен рядок містить 3 вершини, розділені пробілами, щоб утворити трикутник, наприклад: X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3 |
| .blend | Blender File Format | Blender Foundation | Blender 3D | Формат із відкритим кодом, лише у двійковому форматі |
| .fbx | Autodesk FBX Format | Autodesk | Various | Запатентована. Існують двійкові та ASCII специфікації. |
| .3ds | 3ds Max File | Autodesk | 3ds Max | Поширений, але застарілий формат із жорсткими 16-бітовими обмеженнями на кількість вершин та граней. Ні стандартизований, ні добре документований, але раніше був "фактичним стандартом" для обміну даними. |
| .dae | Digital Asset Exchange (COLLADA) | Sony Computer Entertainment, Khronos Group | N/A | Стенди для "COLLAborative Design Activity". Універсальний формат, призначений для запобігання несумісності. |
| .dgn | MicroStation File | Bentley Systems | MicroStation | Існує два формати файлів dgn: попередня версія 8 та версія 8 (V8) |
| .3dm | Rhino File | Robert McNeel & Associates | Rhinoceros 3D | |
| .dxf, .dwg | Drawing Exchange Format | Autodesk | AutoCAD | |
| .obj | Wavefront OBJ | Wavefront Technologies | Various | Формат ASCII, що описує 3D-геометрію. Вершини всіх граней упорядковані проти годинникової стрілки, що робить нормальні аспекти неявними. Плавні нормалі вказані для кожної вершини. |
| .ply | Polygon File Format | Stanford University | Various | Бінарні та ASCII |
| .pmd | Polygon Movie Maker data | Yu Higuchi | MikuMikuDance | Запатентований бінарний формат файлу для зберігання геометрії гуманоїдної моделі з фальсифікацією, матеріалами та фізичною інформацією. |
| .stl | Stereolithography Format | 3D Systems | Many | Бінарний формат та формат ASCII, спочатку розроблений для допомоги в ЧПК. |
| .amf | Additive Manufacturing File Format | ASTM International | N/A | Як і формат STL, але з доданим природним кольором, матеріалом та підтримкою сузір’їв. |
| .wrl | Virtual Reality Modeling Language | Web3D Consortium | Web Browsers | Стандарт ISO 14772-1: 1997 |
| .wrz | VRML Compressed | Web3D Consortium | Web Browsers | |
| .x3d, .x3db, .x3dv | Extensible 3D | Web3D Consortium | Web Browsers | XML на основі відкритого коду, безкорисна, розширюваного та сумісного; також підтримує інформацію про колір, текстуру та епізод. Стандарт ISO 19775/19776/19777 |
| .x3dz, .x3dbz, .x3dvz | X3D Compressed Binary | Web3D Consortium | Web Browsers | |
| .c4d | Cinema 4D File | MAXON | CINEMA 4D | |
| .lwo | LightWave 3D object File | NewTek | LightWave 3D | |
| .smb | SCOREC apf | RPI SCOREC | PUMI | Паралельні адаптивні неструктуровані 3D-сітки з відкритим кодом для робочих процесів моделювання на основі PDE. |
| .msh | Gmsh Mesh | GMsh Developers | GMsh Project | Відкритий код, що надає опис сітки ASCII для лінійних та поліноміально інтерпольованих елементів у 1 - 3 вимірах. |
| .mesh | OGRE XML | OGRE Development Team | OGRE, purebasic | Відкрите джерело. Доступний бінарний (.mesh) та ASCII (.mesh.xml) формат. Включає дані для анімації вершин та Морф цільової анімації (змішана форма). Дані скелетної анімації в окремому файлі (.skeleton). |
| .veg | Vega FEM tetrahedral mesh | Jernej Barbič | Vega FEM | Відкрите джерело. Зберігає тетраедричну сітку та її властивості матеріалу для моделювання FEM. Доступні формати ASCII (.veg) та бінарні (.vegb). |
| .z3d | Z3d | Oleg Melashenko | Zanoza Modeler | - |
| .vtk | VTK mesh | VTK, Kitware | VTK, Paraview | Відкритий формат, ASCII або двійковий формат, який містить безліч різні поля даних , включаючи дані точок, дані комірок та дані полів. |
| .l4d | LAI4D drawing | Laboratory of Artificial Intelligence for Design | LAI4D | Формат даних ASCII, що описує ієрархічне дерево сутностей. |
Див. також[ред. | ред. код]
- Каркасна модель (англ. Wire-frame model)
- Оператор Ейлера
Зноски[ред. | ред. код]
- ↑ Colin Smith, On Vertex-Vertex Meshes and Their Use in Geometric and Biological Modeling, http://algorithmicbotany.org/papers/smithco.dis2006.pdf
- ↑ Bruce Baumgart, Winged-Edge Polyhedron Representation for Computer Vision. National Computer Conference, May 1975. http://www.baumgart.org/winged-edge/winged-edge.html [Архівовано 29 серпня 2005 у Wayback Machine.]
В іншому мовному розділі є повніша стаття Polygon mesh(англ.). Ви можете допомогти, розширивши поточну статтю за допомогою перекладу з англійської.
|
