Розклад невід'ємних матриць
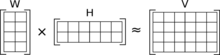
Розклад невід'ємних матриць[1] (NMF(Non-negative matrix factorization)) це група алгоритмів багатовимірного аналізу та лінійної алгебри, де матриця V розкладається в, зазвичай, дві матриці W, H, враховуючи, що жодна з трьох матриць немає від'ємних елементів. Завдяки невід'ємності результуючі матриці легко перевіряються. Крім того, в таких програмах, як обробка аудіо спектрограм даним притаманна ця невід'ємність. Так як проблема немає точних розв'язків, в загальному випадку, зазвичай, знаходять числове наближення.
NMF застосовується в таких областях, як машинне бачення, кластеризація документів, хемометрика, обробка аудіо сигналів і рекомендаційні системи.
Історія[ред. | ред. код]
У хемометриці розклад невід'ємних матриць має довгу історію під назвою «крива самостійного моделювання»[2].У рамках цього фреймворку вектори у правій матриці представляють неперервні криві, а не дискретні вектори. Також ранню роботу з розкладу невід'ємних матриць проводила група фінських вчених в середині 1990-х, під назвою «позитивної матричної факторизації».[3][4] Він став широко відомим як факторизація невід'ємних матриць після того, як Лі і Сунг дослідили властивості алгоритму і опублікували кілька простих і корисних алгоритмів для двох типів факторизацій(множників).[5][6]
Теорія[ред. | ред. код]
Нехай матриця V є добутком матриці W і H
Множення матриць може бути реалізоване як обчислення вектор-стовпчиків матриці V,у вигляді лінійної комбінації вектор-стовпчиків матриці W використовуючи коефіцієнти, що відповідають векторам-рядкам матриці H.Тобто, кожен стовпець V може бути обчислено таким чином:
де vi — і-ий вектор-стовпчик матриці V, a hi — і-ий вектор-стовпчик матриці H.
При множенні матриць, розміри матриць-множників можуть бути значно меншими від розмірів матриці-результата і саме ця властивість формує основну властивість NMF-алгоритму. Тобто, NMF генерує матриці-множники, які набагато менші в порівнянні з вихідною матрицею. Наприклад, коли V розміру m×n, W — m×p, a H — p×n, то p може бути значно меншим від n i m.
Приклад на основі текстового аналізу: •Нехай матриця V має 10000 рядків і 500 стовпчиків, де слова є в рядках, а документи- стовпчиками. Тобто є 500 проіндексованих документів по 100000 слів. •Припустимо, нам потрібно знайти алгоритм, що дає 10 можливостей для того, щоб генерувати матриці W з 10000 рядків і 10 стовпців і коефіцієнти матриці H з 10 рядків і 500 стовпців. •Добуток W на H має розмірність 10000 на 500 і, якщо розклад спрацював правильно, елементи якого приблизно рівні елементам вихідної матриці V. •З цього випливає, що кожен стовпчик з матриці WH є лінійною комбінацією векторів 10 стовпців W і відповідних рядків з матриці H.
Цей останній пункт є основою NMF, тому що ми можемо розглядати кожен вихідний документ у нашому прикладі, який будується з невеликого набору прихованих функцій. NMF генерує ці функції.
Інколи корисно розглядати вектор стовпчик з властивостей матриці W як архетип документа, що містить набір слів, де значення комірки кожного слова визначає ранг даного слова у функції: чим вище значення слова, тим вище ранг слова в функції. Стовпчик в коефіцієнтах матриці H представляє оригінальний документ зі значенням, що визначає значення документа у функції. Це виконується, бо кожен рядок матриці H представляє функцію(властивість). Тепер ми можемо відновити документ (стовпчик вектор) з заданої матриці лінійною комбінацією властивостей (вектори- стовпчики в W ,де кожне значення рівне значенню клітинки із стовпчика документу у H.
Типи[ред. | ред. код]
Наближений розклад невід'ємних матриць[ред. | ред. код]
Зазвичай кількість стовпців у Wі к-сть рядків у H у NMF вибирається так, щоб WH було наближенням до V. Повний розклад V є двома невід'ємними матрицями W і H а також залишкової U, тобто : V = WH + U.Елементи залишкової матриці можуть бути як від'ємними, так і додатними.
Якщо W іHє меншими, ніж V , то їх легше зберігати і ними маніпулювати. Ще одна причина розкладу V на менші матриці W іH, якщо можна представити елементи V набагато меншою кількістю даних, то можна уявити структури, заховані у цих даних з набагато меншими втратами.
Опуклий розклад невід'ємних матриць[ред. | ред. код]
В стандартному NMF, фактор матриця , i.e., W може бути чим завгодно з цього простору. Опуклий NMF[7] обмежує до опуклої комбінації векторів вхідних даних .Це значно підвищує якість представлених даних W. Крім того, результат фактор матриці H стає більш розрідженим і ортогональним.
Невід'ємний ранг розкладу[ред. | ред. код]
Якщо невід'ємний ранг V рівний рангу, V=WH, то він називається невід'ємним рангом розкладу .[8][9][10] Проблемою у відшуканні NRF для V,є те що така проблема є NP-повною.[11]
Різновиди функцій втрат і регуляризації[ред. | ред. код]
Є різні типи розкладу невід'ємних матриць. Різні типи виникають із використанням різних функцій втрат для вимірювання різниці між V іWH і, можливо, із регуляризацією матриці W і/абоH .[12]
Дві прості функції вивчені Лі і Сунгом — це квадрат помилки (або Фробеніусова норма) і розширення відмінності додатних матриць Кулбека-Лейблера. Кожна відмінність призводить до іншого алгоритму NMF, зазвичай мінімузуючого відмінність за допомогою ітеративного процесу.
Проблема факторизації у випадку NMF з квадратом помилки може записуватись так: Дано матрицю знайти невід'ємні матриці W і H, що мінімізують функцію
Ще один тип NMF для зображень базується на нормі повної варіації.[13]
Online NMF[ред. | ред. код]
Багато стандартних алгоритмів NMF аналізують всі дані разом, тобто вся матриця доступна з самого початку. Це може бути незадовільним в додатках, де є занадто багато даних, щоб поміститися в пам'яті або де дані представлені в потоковому вигляді. Прикладом таких може бути колаборативна фільтрація у рекомендаційній системі, де може бути багато користувачів і багато предметів, для рекомендацій, і це було б неефективно перерахувати все, коли один користувач або один елемент буде додано в систему. Функція втрат для оптимізації в таких випадках може або не може бути такою ж, як і для стандартного NMF, але алгоритми повинні бути досить різні.[14][15]
Алгоритми[ред. | ред. код]
Є кілька способів знаходження W and H :правило мультиплікативного оновлення Лі і Сунга,[6] було популярним методом з простою реалізацією. З того часу було розроблено ще кілька інших алгоритмів.
Кілька вдалих алгоритмів базуються на невід'ємних найменших квадратах non-negative least squares: на кожному кроці цього алгоритму, спочатку H є фіксованою, а W знаходиться методом невід'ємних найменших квадратів, тодіW стає фіксованою, а H знаходиться аналогічно. Процедура знаходження W і H може бути такою ж[16] або відмінною, від варіанту регуляризації у NMF одної з W іH.[17] Конкретні підходи включають Метод найшвидшого спуску,[16][18] метод активної множини,[19][20] а також метод повороту головного блоку.[21]
Алгоритми, що доступні зараз є не зовсім оптимальними, бо вони можуть тільки гарантувати знаходження локального мінімуму, порівняно з глобольним мінімумом у функції втрат. Швидше за все оптимальний алгоритм навряд чи буде знайдено в найближчому майбутньому, так як проблема узагальнює проблему K-засобів кластеризації, яка, як відомо єNP-повною.[22] Проте, в багатьох додатках з добування даних, локальний мінімум є корисним.
Точний NMF[ред. | ред. код]
Точний розв'язок для варіантів NMF можна очікувати (за поліноміальний час) коли на матрицю V накладаються додаткові обмеження. Поліноміальний алгоритм для знаходження невід'ємного рангу факторизації, якщо V містить одночлен субматрицю рангу, рівного за рангом даній(Кемпбелл і Пул в 1981 році).[23] Kalofolias and Gallopoulos (2012)[24] вирішити симетричний аналог цієї проблеми, де V симетрична і містить діагональ основної субматриці рангу г. Їх алгоритм виконується зі складністю O(rm²) при високій щільності. Arora, Ge, Halpern, Mimno, Moitra, Sontag, Wu, & Zhu (2013) продемонстрували точний поліноміальний алгоритм NMF, який працює у випадку, де один з факторів W задовольняє умову роздільності.[25]
Посилання[ред. | ред. код]
- ↑ Tandon, Rashish; Suvrit Sra (2010). Sparse nonnegative matrix approximation: new formulations and algorithms (PDF). TR.
- ↑ William H. Lawton; Edward A. Sylvestre (1971). Self modeling curve resolution. Technometrics. 13 (3): 617+. doi:10.2307/1267173.
- ↑ P. Paatero, U. Tapper (1994). Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. Environmetrics. 5 (2): 111—126. doi:10.1002/env.3170050203.
- ↑ Pia Anttila, Pentti Paatero, Unto Tapper, Olli Järvinen (1995). Source identification of bulk wet deposition in Finland by positive matrix factorization. Atmospheric Environment. 29 (14): 1705—1718. doi:10.1016/1352-2310(94)00367-T.
- ↑ Daniel D. Lee and H. Sebastian Seung (1999). Learning the parts of objects by non-negative matrix factorization. Nature. 401 (6755): 788—791. doi:10.1038/44565. PMID 10548103.
- ↑ а б Daniel D. Lee and H. Sebastian Seung (2001). Algorithms for Non-negative Matrix Factorization. Advances in Neural Information Processing Systems 13: Proceedings of the 2000 Conference. MIT Press. с. 556—562.[недоступне посилання з червня 2019]
- ↑ C Ding, T Li, MI Jordan, Convex and semi-nonnegative matrix factorizations, IEEE Transactions on Pattern Analysis and Machine Intelligence, 32, 45-55, 2010
- ↑ Berman, A.; R.J. Plemmons (1974). Inverses of nonnegative matrices. Linear and Multilinear Algebra. 2: 161—172. doi:10.1080/03081087408817055.
- ↑ A. Berman, R.J. Plemmons (1994). Nonnegative matrices in the Mathematical Sciences. Philadelphia: SIAM.
- ↑ Thomas, L.B. (1974). Problem 73-14, Rank factorization of nonnegative matrices. SIAM rev. 16 (3): 393—394. doi:10.1137/1016064.
- ↑ Vavasis, S.A. (2009). On the complexity of nonnegative matrix factorization. SIAM J. Optim. 20: 1364—1377. doi:10.1137/070709967.
- ↑ Inderjit S. Dhillon, Suvrit Sra (2005). Generalized Nonnegative Matrix Approximations with Bregman Divergences (PDF). NIPS. Архів оригіналу (PDF) за 7 серпня 2011. Процитовано 2 червня 2015.
- ↑ DOI:10.1016/j.neucom.2008.01.022
Нема шаблону {{Cite doi/10.1016/j.neucom.2008.01.022}}.заповнити вручну - ↑ Архівована копія (PDF). Архів оригіналу (PDF) за 24 вересня 2015. Процитовано 2 червня 2015.
{{cite web}}: Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання) - ↑ http://portal.acm.org/citation.cfm?id=1339264.1339709
- ↑ а б DOI:10.1162/neco.2007.19.10.2756
Нема шаблону {{Cite doi/10.1162/neco.2007.19.10.2756}}.заповнити вручну - ↑ Hoyer, Patrik O. (2002). Non-negative sparse coding. Proc. IEEE Workshop on Neural Networks for Signal Processing. arXiv:cs/0202009.(англ.) Наведено за англійською вікіпедією.
- ↑ DOI:10.1109/TNN.2007.895831
Нема шаблону {{Cite doi/10.1109/TNN.2007.895831}}.заповнити вручну - ↑ Rainer Gemulla; Erik Nijkamp; Peter J Haas; Yannis Sismanis (2011). Large-scale matrix factorization with distributed stochastic gradient descent. Proc. ACM SIGKDD Int'l Conf. on Knowledge discovery and data mining. с. 69—77.(англ.) Наведено за англійською вікіпедією.
- ↑ Hyunsoo Kim and Haesun Park (2008). Nonnegative Matrix Factorization Based on Alternating Nonnegativity Constrained Least Squares and Active Set Method (PDF). SIAM Journal on Matrix Analysis and Applications. 30 (2): 713—730. doi:10.1137/07069239x. Архів оригіналу (PDF) за 13 жовтня 2015. Процитовано 2 червня 2015.
- ↑ Jingu Kim and Haesun Park (2011). Fast Nonnegative Matrix Factorization: An Active-set-like Method and Comparisons (PDF). SIAM Journal on Scientific Computing. 33 (6): 3261—3281. doi:10.1137/110821172.[недоступне посилання з квітня 2019]
- ↑ Ding, C. and He, X. and Simon, H.D., (2005). On the equivalence of nonnegative matrix factorization and spectral clustering. Proc. SIAM Data Mining Conf. 4: 606—610. doi:10.1137/1.9781611972757.70.
- ↑ Campbell, S.L.; G.D. Poole (1981). Computing nonnegative rank factorizations. Linear Algebra Appl. 35: 175—182. doi:10.1016/0024-3795(81)90272-x.
- ↑ Kalofolias, V.; Gallopoulos, E. (2012). Computing symmetric nonnegative rank factorizations. Linear Algebra Appl. 436: 421—435. doi:10.1016/j.laa.2011.03.016. Архів оригіналу за 24 вересня 2015. Процитовано 2 червня 2015.
- ↑ Arora, Sanjeev; Ge, Rong; Halpern, Yoni; Mimno, David; Moitra, Ankur; Sontag, David; Wu, Yichen; Zhu, Michael (2013). A practical algorithm for topic modeling with provable guarantees. Proceedings of the 30th International Conference on Machine Learning. arXiv:1212.4777. Архів оригіналу за 2 квітня 2015. Процитовано 2 червня 2015.
Додатково[ред. | ред. код]
- J. Shen, G. W. Israël (1989). A receptor model using a specific non-negative transformation technique for ambient aerosol. Atmospheric Environment. 23 (10): 2289—2298. doi:10.1016/0004-6981(89)90190-X.
- Pentti Paatero (1997). Least squares formulation of robust non-negative factor analysis. Chemometrics and Intelligent Laboratory Systems. 37 (1): 23—35. doi:10.1016/S0169-7439(96)00044-5.
- Raul Kompass (2007). A Generalized Divergence Measure for Nonnegative Matrix Factorization. Neural Computation. 19 (3): 780—791. doi:10.1162/neco.2007.19.3.780. PMID 17298233.
- Liu, W.X. and Zheng, N.N. and You, Q.B. (2006). Nonnegative Matrix Factorization and its applications in pattern recognition (PDF). Chinese Science Bulletin. 51 (17–18): 7—18. doi:10.1007/s11434-005-1109-6.[недоступне посилання]
- Ngoc-Diep Ho, Paul Van Dooren and Vincent Blondel (2008). Descent Methods for Nonnegative Matrix Factorization. arXiv:0801.3199 [cs.NA].
- Andrzej Cichocki, Rafal Zdunek and Shun-ichi Amari (2008). Nonnegative Matrix and Tensor Factorization. IEEE Signal Processing Magazine. 25 (1): 142—145. doi:10.1109/MSP.2008.4408452.
- Cédric Févotte, Nancy Bertin, and Jean-Louis Durrieu (2009). Nonnegative Matrix Factorization with the Itakura-Saito Divergence: With Application to Music Analysis. Neural Computation. 21 (3): 793—830. doi:10.1162/neco.2008.04-08-771. PMID 18785855.
- Ali Taylan Cemgil (2009). Bayesian Inference for Nonnegative Matrix Factorisation Models. Computational Intelligence and Neuroscience. 2009 (2): 1. doi:10.1155/2009/785152. PMC 2688815. PMID 19536273.
{{cite journal}}: Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання)[недоступне посилання]







