Оцінка густини
| Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. (вересень 2015) |
Оці́нка густини́ (англ. density estimation) в теорії ймовірностей та статистиці — це побудова оцінки неспостережуваної підлеглої функції густини ймовірності на основі спостережуваних даних. Ця неспостережувана функція густини розглядається як густина, відповідно до якої розподілено велику сукупність, а дані зазвичай розглядаються як випадкова вибірка з тієї сукупності.
Для оцінки густини застосовують ряд підходів, включно з вікном Парцена — Розенблатта та рядом методик кластеризації даних, включно з векторним квантуванням[en]. Найпростішою формою оцінки густини є загрублена гістограма.
Приклад оцінки густини[ред. | ред. код]
Ми розглядатимемо записи про випадки діабету. Наступне є дослівною цитатою з опису набору даних:
| Сукупність жінок віком щонайменше 21 рік з індіанського роду піма, що живуть поблизу Фініксу в Аризоні, перевірялася на цукровий діабет відповідно до критеріїв Всесвітньої організації охорони здоров'я. Дані було зібрано Національним інститутом діабету та дигестивних та ниркових захворювань США[en]. Ми використали 532 повні записи.[1][2] |
В цьому прикладі ми будуємо три оцінки густини для glu (концентрації глюкози в плазмі): одну умовну при наявності діабету, другу умовну при відсутності діабету, та третю безумовну відносно діабету. Умовні оцінки густини потім використовуються для побудови ймовірності діабету в залежності від glu.
Дані glu було отримано з програмного пакету MASS[3] мовою програмування R. В R ?Pima.tr та ?Pima.te дають повний звіт про дані.
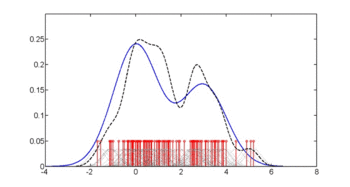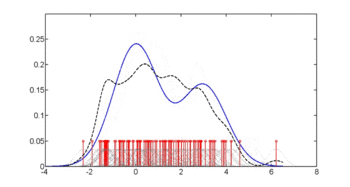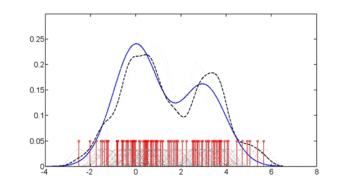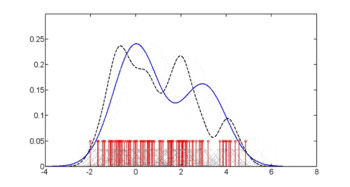
Середнім значенням glu у випадках діабету є 143.1, а стандартним відхиленням — 31.26. Середнім значенням glu у випадках не-діабету є 110.0, а стандартним відхиленням — 24.29. З цього ми бачимо, що в даному наборі даних випадки діабету пов'язано з вищими рівнями glu. Це можна зробити яснішим за допомогою графіків оцінюваних функцій густини.
Перший малюнок показує оцінки густини p(glu | diabetes=1), p(glu | diabetes=0), та p(glu). Ці оцінки густини є ядровими оцінками густини із застосуванням ґаусового ядра. Тобто, в кожній точці даних розташовано ґаусову функцію густини, а потім обчислено суму функцій густини над усім діапазоном даних.
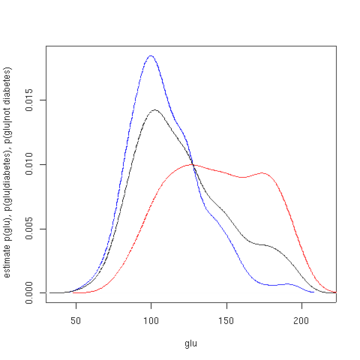
З густини glu в залежності від діабету за допомогою правила Баєса ми можемо отримати ймовірність діабету в залежності від glu. Для стислості «diabetes» у цій формулі скорочено до «db.».
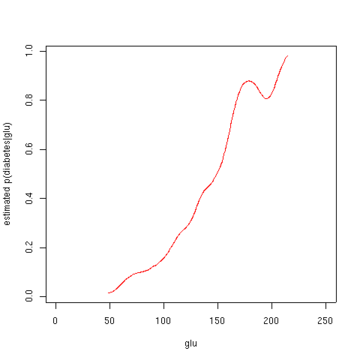
Другий малюнок показує оцінювану апостеріорну ймовірність p(diabetes=1 | glu). З цих даних виявляється, що підвищений рівень glu пов'язаний із діабетом.
Сценарій для прикладу[ред. | ред. код]
Наступні команди R створять наведені вище малюнки. Ці команди можна ввести до командного запрошення застосуванням копіювання та вставлення.
library(MASS)
data(Pima.tr)
data(Pima.te)
Pima <- rbind (Pima.tr, Pima.te)
glu <- Pima[, 'glu']
d0 <- Pima[, 'type'] == 'No'
d1 <- Pima[, 'type'] == 'Yes'
base.rate.d1 <- sum(d1) / (sum(d1) + sum(d0))
glu.density <- density (glu)
glu.d0.density <- density (glu[d0])
glu.d1.density <- density (glu[d1])
glu.d0.f <- approxfun(glu.d0.density$x, glu.d0.density$y)
glu.d1.f <- approxfun(glu.d1.density$x, glu.d1.density$y)
p.d.given.glu <- function(glu, base.rate.d1)
{
p1 <- glu.d1.f(glu) * base.rate.d1
p0 <- glu.d0.f(glu) * (1 - base.rate.d1)
p1 / (p0 + p1)
}
x <- 1:250
y <- p.d.given.glu (x, base.rate.d1)
plot(x, y, type='l', col='red', xlab='glu', ylab='estimated p(diabetes|glu)')
plot(density(glu[d0]), col='blue', xlab='glu', ylab='estimate p(glu),
p(glu|diabetes), p(glu|not diabetes)', main=NA)
lines(density(glu[d1]), col='red')
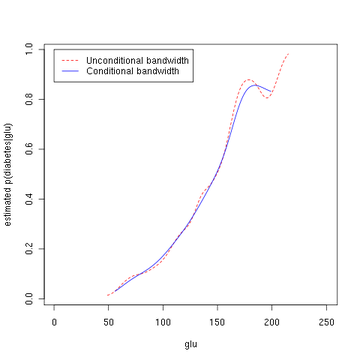
Зауважте, що наведена вище оцінка умовної густини використовує ширини смуг пропускання (англ. bandwidth), що є оптимальними для безумовних густин. Як альтернативу можна застосовувати метод Хола, Расіна та Лі (англ. Hall, Racine and Li, 2004)[4] та пакет R np[5] для автоматичного (керованого даними) вибору ширини смуги пропускання, що є оптимальним для оцінки умовних густин; див. введення до пакету np у начерку про нього.[6] Наступні команди R використовують функцію npcdens() для отримання оптимального згладжування. Зауважте, що реакція "Yes"/"No" є фактором.
library(np)
fy.x <- npcdens(type~glu, nmulti=1, data=Pima)
Pima.eval <- data.frame(type=factor("Yes"),
glu=seq(min(Pima$glu), max(Pima$glu), length=250))
plot(x, y, type='l', lty=2, col='red', xlab='glu',
ylab='estimated p(diabetes|glu)')
lines(Pima.eval$glu, predict(fy.x, newdata=Pima.eval), col="blue")
legend(0, 1, c("Unconditional bandwidth", "Conditional bandwidth"),
col=c("red", "blue"), lty=c(2, 1))
Третій малюнок використовує оптимальне згладжування методом Хола, Расіна та Лі,[4] вказуючи, що ширина смуги пропускання безумовної густини, використана у другому малюнку вище, видає оцінку умовної густини, що може бути дещо недозгладженою.
Див. також[ред. | ред. код]
- Ядрова оцінка густини розподілу
- Середня інтегрована квадратична помилка[en]
- Гістограма
- Багатовимірна ядрова оцінка густини[en]
- Оцінка спектральної густини[en]
- Ядрове включення розподілів[en]
Примітки[ред. | ред. код]
- ↑ Diabetes in Pima Indian Women - R documentation. (англ.)
- ↑ Smith, J. W., Everhart, J. E., Dickson, W. C., Knowler, W. C. and Johannes, R. S. (1988). R. A. Greenes (ред.). Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. Proceedings of the Symposium on Computer Applications in Medical Care (Washington, 1988). Los Alamitos, CA: IEEE Computer Society Press: 261—265. PMC 2245318. (англ.)
- ↑ Support Functions and Datasets for Venables and Ripley's MASS. (англ.)
- ↑ а б Peter Hall; Jeffrey S. Racine; Qi Li (2004). Cross-Validation and the Estimation of Conditional Probability Densities. Journal of The American Statistical Association. 99 (468): 1015—1026. (англ.)
- ↑ Пакет np — Пакет R, що пропонує низку непараметричних та напівпараметричних ядрових методів, що легко обробляють суміш неперервних, невпорядкованих та впорядкованих типів даних факторів.
- ↑ Tristen Hayfield; Jeffrey S. Racine. The np Package (PDF). (англ.)
Джерела[ред. | ред. код]
- Brian D. Ripley (1996). Pattern Recognition and Neural Networks. Cambridge: Cambridge University Press. ISBN 978-0521460866. (англ.)
- Trevor Hastie[en], Robert Tibshirani[en], and Jerome Friedman. The Elements of Statistical Learning. New York: Springer, 2001. ISBN 0-387-95284-5. (See Chapter 6.) (англ.)
- Qi Li and Jeffrey S. Racine. Nonparametric Econometrics: Theory and Practice. Princeton University Press, 2007, ISBN 0-691-12161-3. (See Chapter 1.) (англ.)
- D.W. Scott. Multivariate Density Estimation. Theory, Practice and Visualization. New York: Wiley, 1992. (англ.)
- B.W. Silverman[en]. Density Estimation. London: Chapman and Hall, 1986. ISBN 978-0-412-24620-3 (англ.)
Посилання[ред. | ред. код]
- CREEM: Centre for Research Into Ecological and Environmental Modelling Завантаження вільних програмних пакетів для оцінки густини Distance 4 (від Research Unit for Wildlife Population Assessment "RUWPA") та WiSP.
- UCI Machine Learning Repository Content Summary (Див. оригінальний набір даних з 732 записів у "Pima Indians Diabetes Database" та додаткові примітки.)
- Код MATLAB для одновимірної та двовимірної оцінки густини
- libAGF програма на C++ для мінливої ядрової оцінки густини[en].
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
