Сортування злиттям

Матеріал з Вікіпедії — вільної енциклопедії.

Сортування злиттям — алгоритм сортування, в основі якого лежить принцип Розділяй та володарюй. В основі цього способу сортування лежить злиття двох упорядкованих ділянок масиву в одну впорядковану ділянку іншого масиву. Злиття двох упорядкованих послідовностей можна порівняти з перебудовою двох колон солдатів, вишикуваних за зростом, в одну, де вони також розташовуються за зростом. Якщо цим процесом керує офіцер, то він порівнює зріст солдатів, перших у своїх колонах і вказує, якому з них треба ставати останнім у нову колону, а кому залишатися першим у своїй. Так він вчиняє, поки одна з колон не вичерпається — тоді решта іншої колони додається до нової.

Підчас сортування в дві допоміжні черги з основної поміщаються перші дві відсортовані підпослідовності, які потім зливаються в одну і результат записується в тимчасову чергу. Потім з основної черги беруться наступні дві відсортовані підпослідовності і так до тих пір доки основна черга не стане порожньою. Після цього послідовність з тимчасової черги переміщається в основну чергу. І знову продовжується сортування злиттям двох відсортованих підпослідовностей. Сортування триватиме до тих пір поки довжина відсортованої підпослідовності не стане рівною довжині самої послідовності.

[ред.] Алгоритм сортування

Нехай у масиві Y з елемента Y[m] починається впорядкована ділянка довжиною s, а з елемента Y[m+s] – впорядкована ділянка довжини r. Наприклад,

Результатом злиття повинна бути ділянка довжини r+s у масиві X:

Тепер розглянемо сортування масиву A злиттям. На першому кроці елементи A[1], … , A[n] копіюються в допоміжний масив B[1], … , B[n]. Його елементи розглядаються парами B[1] і B[2], B[3] і B[4] тощо як упорядковані послідовності довжиною lp = 1 і зливаються за допомогою процедури mrg в масив A. Тепер там є впорядковані ділянки довжиною 2. За непарного n останній елемент A[n] залишається без змін як послідовність довжиною 1. На наступному кроці після копіювання в масив B зливаються пари упорядкованих ділянок B[1]B[2] і B[3]B[4], B[5]B[6] і B[7]B[8] тощо. З'являються впорядковані ділянки довжиною 4. Нехай t=nmod4 – довжина залишку масиву після останньої повної четвірки елементів. При t=1 або t=2 останні t елементів утворюють упорядковану ділянку після попереднього кроку. При t=3 зливаються упорядкована пара B[n-1]B[n-2] та ділянка B[n] у ділянку довжиною t. Кроки повторюються з подвоєнням довжин упорядкованих ділянок lp, поки lp < n. Розглянемо сортування злиттям масиву <11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1> довжини n=11. Упорядковані послідовності в ньому вказуються в дужках <>, а пари таких, що зливаються, відокремлені ";": < <11><10> ; <9><8> ; <7><6> ; <5><4> ; <3><2> ; <1> >, lp=1 < <10, 11><8, 9> ; <6, 7><4, 5> ; <2, 3><1> >, lp=2 < <8, 9, 10, 11><4, 5, 6, 7>;<1, 2, 3> >, lp=4 < <4, 5, 6, 7, 8, 9, 10, 11><1, 2, 3> >, lp=8 <1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11>, lp=16, lp³ n. Як бачимо, нам знадобилося 4 кроки злиття для того, щоб одержати впорядований масив. Очевидно, що після k-го кроку впорядковані ділянки мають довжину lp=2k. Якщо 2k=n, то масив упорядковано. Якщо 2k>n, але 2k-1<n, то при виконанні останнього кроку мають місце співвідношення lp = 2k-1 = 2k / 2 > n/2, npp = 0, tl = n > lp, і злиття ділянки довжиною lp та залишку довжиною n-lp дає впорядкований масив. Оцінимо складність наведеного алгоритму. При кожному виконанні тіла циклу while значення всіх елементів масиву копіюються в допоміжний масив і назад по одному разу, тобто виконується O(n) елементарних дій. Після останнього k-го кроку 2k<2n, тобто k<1+logn, і це означає, що тіло циклу while виконується 1+ëlog2nû =O(logn) разів. Отже, складність алгоритму оцінюється як O(nlogn). Запишемо в таблицю значення виразів n, n(n-1)/2, n(1+ë log2nû ) та округлене відношення r двох останніх:

Як бачимо, кожне зростання n у 10 разів веде до зростання n(n-1)/2 та n(1+ë log2nû ) приблизно в 100 й 14 разів відповідно, і за n=10000 сортування злиттям виконується в сотні разів скоріше, ніж бульбашкове! Зауважимо, що в наведеному алгоритмі сортування злиттям копіювання масиву в допоміжний указано лише для того, щоб ідею алгоритму було простіше сприйняти. Цей алгоритм нескладно переробити так, щоб замість копіювання в додатковий масив відбувалося злиття в нього упорядкованих ділянок. Отже, на кроках з номерами 1, 3, 5, … має відбуватися злиття в допоміжний масив, а на кроках 2, 4, 6, … – злиття в протилежному напрямку. Переробка алгоритму залишається вправою. Сортування злиттям можна задати рекурсивно: масив поділяється на дві приблизно рівні частини, які після сортування (тим самим способом – ось рекурсія!) зливаються. Коли ж довжина частини масиву зменшується до 1, відбувається просто повернення з рекурсії. Цей алгоритм уточнюється наступною процедурою Mrgrec. На відміну від процедури Merges, вона має два параметри-масиви (той, що сортується, та допоміжний), а також два числові параметри (початок і кінець частини масиву, яка сортується). Крім того, спочатку відбувається злиття ділянок основного масиву в допоміжний, а потім копіювання в основний: Ця функція набагато коротше нерекурсивної функції, але виконання її довше. Власне сортування починається лише після повернення з викликів, у яких l=r, а це практично "середина дистанції". Завершуючи описання сортування злиттям, скажемо, що цей алгоритм є першим із ефективних алгоритмів сортування. У 1945 році його винайшов Джон фон Нейман, один із піонерів програмування.

[ред.] Псевдокод алгоритму

Процедура здійснює часткове впорядкування масиву , впорядковуючи його елементи з p-го по q-ий здійснить впорядкування всього масиву).

1 if 
2    then return
3   
4 
5 
6 

використовує допоміжну процедуру , що здійснює об'єднання частин масиву A з p-го по c-ий елемент і з c+1-го по q-ий елемент в один впорядкований підмасив. Для цього аикористовується один додатковий масив такої ж довжини як і (В деяких реалізаціях вдвічі коротший за — мінімально можлива його довжина).

1 
2 
3 for  to 
4     do if  або ( і )
5           then 
6                
7           else 
8                
9 for  to 
10    do 

[ред.] Аналіз алгоритму

Час роботи алгоритму по впорядкуванню елементів задовільняє рекурентному співвідношенню:

, де — час на впорядкування половини масиву, — час на злиття цих половинок.

Враховуючи, що , розв'язком співвідношення є .

Крім того, алгоритм потребує для своєї роботи додаткової пам'яті.

Алгоритм не міняє порядок розташування однакових елементів, а отже він є стабільним.

[ред.] Можливі оптимізації

Швидкість алгоритму є асимптотично оптимальною. Але її можна пришвидшити в константну кількість разів.

• Оптимізація впорядкування невеликих частин масиву — невеликі частини масиву (наприклад, при q-p<50) впорядковувати сортуванням вставкою.
• Оптимізація кількості копіювань елементів — при злитті двох впорядкованих масивів в один, кожен елемент копіюється два рази (спочатку у тимчасовий масив, а потім знову у початковий). Кількість копіювань можна зменшити удвічі, якщо по черзі використовувати для об'єднання початковий і тимчасовий масиви. Тоді можна не виконвати зайві операції копіювання (рядки 9-10 процедури Merge).

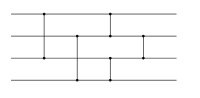
[ред.] Робота алгоритму

Схема алгоритму для конкретного прикладу послідовності

Проілюструємо алгоритм сортування на такій послідовності: 42 5 30 36 25 10 49 0 0 На початку сортування відсортовані підпослідовності містять в собі по одному елементу.

Крок 1: 5 42 | 30 36 | 10 25 | 37 49 | 0 0

Крок 2: 5 30 36 42 | 10 25 37 49 | 0 0

Крок 3: 5 10 25 30 36 37 42 49 | 0 0

Крок 4: 0 0 5 10 25 30 36 37 42 49

[ред.] Тестування алгоритму

Для перевірки правильності сортування звіримо сортування проведене програмою з сортуванням за даним алгоритмом вручну.

Проведемо сортування наступної послідовності: 56 19 3 95 23 17 38 44 69 73 84

На початку сортування послідовність є розбита на відсортовані підпослідовності по одному елементу в кожній.

56 | 19 | 3 | 95 | 23 | 17 | 38 | 44 | 69 | 73 | 84

далі кожні дві підпослідовності зливаються в одну відсортовану підпослідовність : 19 56 | 3 95 | 17 23 | 38 44 | 69 73 | 84

на наступному кроці отримаємо наступний результат злиття: 3 19 56 95 | 17 23 38 44 | 69 73 84 |

потім: 3 17 19 23 38 44 56 95 | 69 73 84 |

на останньому кроці отримаємо відсортовану послідовність: 3 17 19 23 38 44 56 69 73 84 | 95

Послідовність була відсортована за 4 кроки.

[ред.] Реалізація (Паскаль)

<tt>procedure MergeSort( var  ar1, ar2: array  of Integer; min, max: Integer);
 
var
 
middle, int1, int2, int3: Integer;
 
begin
 
if min<max then begin //інакше массив складається 
 
//з одного елемента і є впорядкованим.
 
middle:=min div 2+max div 2;
 
// рекурсивно сортуєму підсписки
 
MergeSort(ar1, ar2, min, middle);
 
MergeSort(ar1, ar2, middle+1, max);
 
 
int1:=min; //вказівник на 1-й массив
 
int2:=middle+1; //вказівник на 2-й массив
 
int3:=min; //вказівник на обєднаний масив
 
 
//обєднання сортованих масивів
while (int1<=middle) and (int2<=max) do begin
 
if ar1[int1] then begin
 
ar2[int3]:=ar1[int1];
 
int1:=int1+1;
 
end
 
else begin
 
ar2[int3]:=ar1[int2];
 
int2:=int2+1;
 
end;
 
inc(int3);
 
end;
 
// очистка не пустого списка
 
while (int1<=middle) do begin
 
ar2[int3]:=ar1[int1];
 
int1:=int1+1;
 
int3:=int3+1;
 
 
end;
 
while (int2<=middle) do begin
 
ar2[int3]:=ar1[int2];
 
int2:=int2+1;
 
int3:=int3+1;
 
end;
end;
//прирівнювання входящих массивів
 
for int1:=min to max do
 
ar1[int1]:=ar2[int1];
 
end;</tt>

Ще один приклад:

uses SysUtils;
const n=10;
type mas=array[1..n] of integer;
var x1,x2:mas;
    i:integer;
procedure mrg(var y,x:mas; m,s,r:integer);
var mr,k,i,j:integer;
begin
 mr:=m+s;
 i:=m;
 j:=mr;
 for k:=m to m+s+r-1 do
  if i>m+s-1 then
  begin
  x[k]:=y[j];
  j:=j+1;
  end
   else
   if j>mr+r-1 then
    begin
    x[k]:=y[i];
    i:=i+1;
    end
    else if y[i]<y[j] then
    begin
    x[k]:=y[i];
    i:=i+1;
    end
    else
     begin
     x[k]:=y[j];
     j:=j+1;
     end;end;
     procedure Mrg_rec(var a,b:mas; l,r:integer);
      var m,k:integer;
     begin
     if l>=r then exit;
     m:=(l+r)div 2;
     Mrg_rec(a,b,l,m);
     Mrg_rec(a,b,m+1,r);
     mrg(a,b,l,m-l+1,r-m);
     for k:=1 to r do
     a[k]:=b[k];
     end;
begin
randomize;
for i:=1 to n do
 x1[i]:=random(10)-5;
for i:=1 to n do
 writeln(x1[i]);
mrg_rec(X1,X2,1,n);
writeln;
 for i:=1 to n do
 writeln(x1[i]);
 readln; writeln('that''s all'); readln;
end.

А це - складний приклад реалізації сортування масивів:

program SortArrays;
{$APPTYPE CONSOLE}
uses SysUtils;
type Massive=array[1..25] of integer;
var A:massive; n:integer;
procedure RndArrInput (var a1:massive; n1:integer);
var i1:integer;
begin
Randomize;
 for i1:=1 to n1 do
 a1[i1]:=20-random(20);
end;
procedure ArrOutPut(a2:massive; n2:integer);
 var i2:integer;
begin
 for i2:=1 to n2 do
 write(a2[i2],' ');
end;
procedure Annihilate(var an:massive; nn:integer);
var i_:integer;
begin
 for i_:=1 to nn do
 an[i_]:=0;
end;
procedure MergeUnion(const a:massive; N_a:integer;
  const b:massive; N_b:integer; var c:massive; {var N_c:integer}start:integer);
  var i_a,i_b,i_c:integer;
  Begin
  i_a:=1; i_b:=1; i_c:={1;}start; 
  while (i_a<=N_a)and(i_b<=N_b) do begin
 
  if a[i_a]<b[i_b] then begin
 
  c[i_c]:=a[i_a];
  inc(i_a);
  inc(i_c);
  end else
  if a[i_a]>b[i_b] then begin
 
  c[i_c]:=b[i_b];
  inc(i_b);
  inc(i_c);
  end else begin (* a[i_a]=b[i_b] *)
 
  c[i_c]:=a[i_a];
 inc(i_a);
  {inc(i_b);} //we shouldn't write the equal value only once
 inc(i_c); c[i_c]:=b[i_b]; inc(i_b); inc(i_c);
 end
 end;
 
 while (i_a<=N_a) do begin
  c[i_c]:=a[i_a];
  inc(i_a);
  inc(i_c);
 end;
 
  while (i_b<=N_b) do begin
   c[i_c]:=b[i_b];
   inc(i_b);
   inc(i_c);
   end;
   End;
procedure MergeSort(var a3:massive; n3:Integer);
var hlp1,hlp2,hlp3:massive; cnt:integer; LineChanged:Boolean;
    cur_1, cur_2:integer; i:integer;
    cur:Integer; pnt:integer; hlp_cur:integer; WtoHlp1,WtoHlp2:Boolean;
begin
 Annihilate(hlp1,n3);
 Annihilate(hlp2,n3);
 Annihilate(hlp3,n3);
 cnt:=1; LineChanged:=true;
 while LineChanged do
 begin
   pnt:=1; lineChanged:=false;
   while pnt<=n3 do
  begin
  cur:=1; WtoHlp1:=false; Wtohlp2:=false; cur_1:=0; cur_2:=0;
  while (cur<=cnt)and(pnt<=n3) do
    begin
     hlp1[cur]:=a3[pnt];
     inc(pnt);
     inc(cur); inc(cur_1);
     WtoHlp1:=true;
    end;
   cur:=1;
  while (cur<=cnt)and(pnt<=n3) do
    begin
     hlp2[cur]:=a3[pnt];
     inc(pnt);
     inc(cur); inc(cur_2);
     WtoHlp2:=true; lineChanged:=true;
    end;
    if WToHlp1 and WToHlp2 then
    MergeUnion(hlp1,cur_1,hlp2,cur_2,hlp3,pnt-{2*cnt}(cur_1+cur_2));
    if WToHlp1 and not(WtoHlp2) then
     for i:=1 to cur_1 do
       begin
      hlp3[pnt-(cur_1+cur_2)]:=hlp1[i];
      inc(pnt);
       end;
//tail-writting. cur_1 is the point, how many elements have we in hlp1.
  end;
  cnt:=cnt*2;
  a3:=hlp3;
 end;{of while LineChanged}
end;{of procedure}
begin
  writeln('enter data:');
  readln(n);
  RndArrInput(a,n);
  ArrOutput(a,n);
  readln;
  MergeSort(a,n);
  readln;
  ArrOutput(a,n);
  readln;
end.

[ред.] Джерела

• Thimas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein. Introduction to Algorithms (2nd ed.) The MIT Press. ISBN 0-07-013151-1

http://www.compdoc.ru/prog/pascal/algorithms_of_sorting_part2/ - Алгоритм