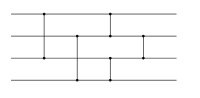
Швидке сортування

Швидке сортування

алгоритм у дії під час сортування списку чисел
Клас	Алгоритм сортування
Структура даних	Різні
Найгірша швидкодія	$O(n^{2})$
Найкраща швидкодія	$O(n\log n)$
Середня швидкодія	$O(n\log n)$
Просторова складність у найгіршому випадку	Залежить від реалізації
Оптимальний	Інколи
Стабільний	Ні

Швидке сортування (англ. Quick Sort) — алгоритм сортування, розроблений Тоні Гоаром, який не потребує додаткової пам'яті і виконує у середньому $\;O(n\log \;n)$ операцій. Однак, у найгіршому випадку робить $O(n^{2})$ порівнянь. Позаяк алгоритм використовує дуже прості цикли і операції, він працює швидше за інші алгоритми, що мають таку ж асимптотичну оцінку складності. Наприклад, зазвичай більш ніж удвічі швидший порівняно з сортуванням злиттям.

Ідея алгоритму полягає в переставлянні елементів масиву таким чином, щоб його можна було розділити на дві частини і кожний елемент з першої частини був не більший за будь-який елемент з другої. Впорядкування кожної з частин відбувається рекурсивно. Алгоритм швидкого сортування може бути реалізований як у масиві, так і в одно або двозв'язному списку.

Швидке сортування є алгоритмом на основі порівнянь і не є стабільним.

Історія

Алгоритм швидкого сортування було розроблено Тоні Гоаром у 1962 під час роботи у маленькій британській компанії Elliott Brothers.

Псевдокод алгоритму

Класичний алгоритм

У класичному варіанті, запропонованому Гоаром, з масиву обирали один елемент, а весь масив розбивали на дві частини за принципом: у першій частині — не більші за даний елемент, в другій — не менші за даний елемент. Процедура $Quicksort(A,p,q)$ здійснює часткове впорядкування масиву $\;A$ з p-го по q-й індекс:

$\;Quicksort(A,p,q)\;$
1 if $p\geq \;q$ return;
2 $r\gets \;A[p]$
3 $i\gets \;p-1$
4 $j\gets \;q+1$
5 while $\;i<j$ do
6       repeat
7             $i\gets \;i+1$
8       until $A[i]\geq \;r$
9       repeat
10            $j\gets \;j-1$
11      until $A[j]\leq \;r$
12      if $\;i<j$
13         then Swap $A[i]\leftrightarrow \;A[j]$
14 $\;Quicksort(A,p,j-1)$
15 $\;Quicksort(A,j+1,q)$

Сучасний алгоритм

Нині в стандартних бібліотеках використовують таку реалізацію алгоритму:

$Partition(A,p,q)\;$
1 $x\gets \;A[q]$
2 $i\gets \;p-1$
3 for $j\gets \;p$ to $\;q-1$
4 do if $A[j]\leq \;x\;$
5     then
6           $i\gets \;i+1$
7           Swap $A[i]\leftrightarrow \;A[j]$
8 Swap $A[i+1]\leftrightarrow \;A[q]$
8 return $\;i+1$

Функція Partition повертає індекс з опорним елементом, що розділяє масив на дві частини; ліву — елементи якої менше опорного елементу, і праву — елементи якої більше опорного елементу. Всередині функції опорним елементом вибирається останній елемент масиву і обхід здійснюється починаючи з першого елементу, прирівнюючи його до опорного.

$Quicksort(A,p,q)\;$
1 if $p\geq \;q$ return;
2 $i\gets \;Partition(A,p,q)$
3 $\;Quicksort(A,p,i-1)$
4 $\;Quicksort(A,i+1,q)$

Аналіз

Час роботи алгоритму сортування залежить від збалансованості, що характеризує розбиття. Збалансованість у свою чергу залежить від того, який елемент обрано як опорний (відносно якого елемента виконується розбиття). Якщо розбиття збалансоване, то асимптотично алгоритм працює так само швидко як і алгоритм сортування злиттям. У найгіршому випадку асимптотична поведінка алгоритму настільки ж погана, як і в алгоритму сортування включенням.

Найгірше розбиття

Найгірша поведінка має місце у тому випадку, коли процедура, що виконує розбиття, породжує одну підзадачу з n-1 елементом, а другу — з 0 елементами. Нехай таке незбалансоване розбиття виникає при кожному рекурсивному виклику. Для самого розбиття потрібен час $\;\Theta (n)$. Тоді рекурентне співвідношення для часу роботи можна записати так:

$\;T(n)=T(n-1)+T(0)+\Theta (n)=T(n-1)+\Theta (n)$

Розв'язком такого співвідношення є $\;T(n)=\Theta (n^{2})$.

Найкраще розбиття

В найкращому випадку процедура Partition ділить задачу на дві підзадачі, розмір кожної не перевищує n/2. Час роботи описується нерівністю:

$T(n)\leq 2T(n/2)+\Theta (n)$

Тоді:

$\;T(n)=O(n\log n)$ — асимптотично найкращий час.

Середній випадок

Математичне очікування часу роботи алгоритму на всіх можливих вхідних масивах є $\;O(n\log n)$, тобто середній випадок ближчий до найкращого.

Модифікації

В середньому алгоритм працює дуже швидко, але на практиці не всі можливі вхідні масиви мають однакову імовірність. Тоді шляхом додання рандомізації вдається отримати середній час роботи в будь-якому випадку.

Рандомізованний алгоритм

В рандомізованному алгоритмі, при кожному розбитті випадковий елемент обирається як опорний:

$Randomized\_Partition(A,p,q)\;$
1 $i\leftarrow Random(p,q)$
2 Поміняти $A[i]\leftrightarrow A[q]$
9 return $\;Partition(A,p,q)$

$Randomized\_Quicksort(A,p,q)\;$
1 if $p\geq \;q$ return;
2 $i\gets \;Randomized\_Partition(A,p,q)$
3 $\;Randomized\_Quicksort(A,p,i-1)$
4 $\;Randomized\_Quicksort(A,i+1,q)$

Реалізація мовою Pascal

Ця процедура, після її оголошення, сортує масив mas, який складається з елементів типу integer.

Procedure QuickSort(first, last :integer);
Var v, x, left, right :integer;
begin
  left := first;
  right := last;
  v := mas[(left + right) div 2];
  while left <= right do
    begin
    while mas[left] < v do
      left := left + 1;
    while mas[right] > v do
      right := right - 1;
    if left <= right then
      begin
        x := mas[left];
        mas[left] := mas[right];
        mas[right] := x;
        left := left + 1;
        right := right - 1;
      end;
    end;
  if first < right then
    QuickSort(first, right);
  if left < last then
    QuickSort(left, last);
end;

Реалізація мовою C++

Ця функція сортує масив array, що містить n елементів, де right = n-1.

right-left+1: +1 для того, аби у виклику QuickSort (array, 0, 1) опорним елементом вибирався правий елемент, що не допустить спробу декрементувати j, коли ця змінна вже рівна 0.

 template <typename T>
 void QuickSort (T array[],
                 size_t const left,
                 size_t const right)
 {

     static T temp;
     size_t i=left, j=right;
     T pivot = array[left + ((right-left+1) >> 1)];

     while (i <= j)
     {
         while (array[i] < pivot) ++i;
         while (array[j] > pivot) --j;

         if (i <= j)
         {
             temp = array[i];
             array[i] = array[j];
             array[j] = temp;
             ++i;
             --j;
         }
     }
     if (j > left)
         QuickSort (array, left, j);
     if (i < right)
         QuickSort (array, i, right);
 }

Реалізація мовою JavaScript

Функція quickSort приймає масив arr як вхідний параметр і повертає відсортований масив.

function quickSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }
  
  const pivot = arr[Math.floor(arr.length / 2)];
  const less = [];
  const greater = [];
  
  for (let i = 0; i < arr.length; i++) {
    if (i === Math.floor(arr.length / 2)) continue
    if (arr[i] < pivot) {
      less.push(arr[i]);
    } else {
      greater.push(arr[i]);
    }
  }
  
  return [...quickSort(less), pivot, ...quickSort(greater)];
}

// Приклад використання:
const array = [5, 3, 1, 6, 2, 4];
const sortedArray = quickSort(array);
console.log(sortedArray);

// Результат
// [1, 2, 3, 4, 5, 6]

Реалізація мовою Ruby

Метод quick_sort приймає масив arr як вхідний параметр і повертає відсортований масив.

def quick_sort(arr)
  return arr if arr.length <= 1

  pivot = arr[arr.length / 2]
  less = []
  greater = []

  arr.each do |element|
    if element < pivot
      less << element
    elsif element > pivot
      greater << element
    end
  end

  return [*quick_sort(less), pivot, *quick_sort(greater)]
end

# Приклад використання:
array = [5, 3, 1, 6, 2, 4]
sorted_array = quick_sort(array)
puts sorted_array

# Результат
# [1, 2, 3, 4, 5, 6]

Література

• Т. Кормен; Ч. Лейзерсон; Р. Рівест; К. Стайн (2009) [1990]. 7 Швидке сортування. Вступ до алгоритмів (вид. 3rd). MIT Press і McGraw-Hill. ISBN 0-262-03384-4.

Посилання

• Реалізація алгоритму швидкого сортування різними мовами програмування [Архівовано 7 лютого 2015 у Wayback Machine.]
• Реалізації алгоритму швидкого сортування різними мовами програмування в стилі грамотного програмування [Архівовано 9 травня 2008 у Wayback Machine.]
• Animated Sorting Algorithms: Quick Sort — графічна демонстрація роботи алгоритму
• Animated Sorting Algorithms: 3-Way Partition Quick Sort — графічна демонстрація алгоритму швидкого сортування з розбиттям масиву на три частини.
• Наочна демонстрація швидкого сортування угорськими танцюристами. [Архівовано 7 червня 2014 у Wayback Machine.]
• Interactive Tutorial for Quicksort [Архівовано 3 лютого 2009 у Wayback Machine.]
• Analyze Quicksort in an online Javascript IDE
• Javascript Quicksort and Bubblesort
• Quicksort applet
• Multidimensional quicksort in Java
• Quicksort tutorial with illustrated examples