Timsort

Матеріал з Вікіпедії — вільної енциклопедії.
Версія від 18:35, 13 лютого 2022, створена TohaomgBot (обговорення | внесок) (Перекладено дати в примітках з англійської на українську)
Перейти до навігації Перейти до пошуку
Timsort
КласАлгоритм сортування
Структура данихМасив
Найгірша швидкодія[1][2]
Найкраща швидкодія[3]
Середня швидкодія
Просторова складність у найгіршому випадку

Timsort — гібридний стабільний алгоритм сортування, який поєднує в собі сортування злиттям та сортування включенням, призначений для ефективної роботи з багатьма видами реальних даних. Він був втілений в життя Тімом Пітерсом у 2002 році для використання у мові програмування Python. Алгоритм знаходить підпослідовності даних, які вже впорядковані, і використовує їх для більш ефективного сортування залишків. Це робиться шляхом об'єднання впорядкованих частин до виконання певних критеріїв. Timsort був стандартним алгоритмом сортування Python з версії 2.3. Він також використовується для сортування масивів не примітивного типу в Java SE 7,[4] на платформі Android[5], у GNU Octave[6], Swift[7], та Rust[8].

Він використовує прийоми з статті Пітера Макілроя 1993 року «Оптимістичне сортування та теоретична складність інформації»[9].

Алгоритм

Timsort був розроблений, щоб скористатися перевагами наборів упорядкованих елементів, які вже існують в більшості реальних даних. Він перебирає елементи, збираючи впорядковані частини і одночасно поміщає ці частини в стек. Щоразу, коли частини зверху стека відповідають критеріям об'єднання, вони об'єднуються. Це триває поки всі дані не будуть пройдені; потім усі впорядковані частини об'єднуються по дві одночасно, і залишається лише один відсортований набір. Перевага об'єднання впорядкованих частин замість об'єднання підмасивів фіксованого розміру (як це робиться традиційним об'єднанням)-це зменшує загальну кількість порівнянь, необхідних для сортування всього масиву.

Кожен набір має мінімальний розмір, який ґрунтується на розмірі вхідних даних і визначається на початку алгоритму. Якщо набір менший за цей мінімальний розмір, використовується сортування включенням для додавання до набору додаткових елементів до досягнення мінімального розміру набору.

Критерії об'єднання

Набори вставляються у стек. Якщо , тоді X і Y об'єднуються і замінюються у стеку. Таким чином, злиття продовжується до тих пір, поки всі набори не задовольнять і. та іі.

Timsort — це стабільний алгоритм сортування (порядок елементів з однаковими значеннями зберігається) і прагне виконувати збалансоване злиття (таким чином злиття об'єднує набори подібного розміру).

Для досягнення стабільності сортування об'єднуються лише послідовні набори. Між двома послідовними наборами всередині набору може бути елемент з однаковим значенням. Об'єднання цих двох наборів змінило б порядок однакових значень. Приклад цієї ситуації ([]- це впорядковані набори): [1 2 2] 1 4 2 [0 1 2]

У гонитві за збалансованим злиттям, Timsort розглядає три набори на вершині стека, X, Y, Z і підтримує інваріанти: і.

іі.

Якщо будь-який з цих інваріантів порушується, Y зливається з меншим з X або Z, і інваріанти перевіряються знову. Після того, як інваріанти задовільнили умову, можна починати пошук нового впорядкованого набору в даних.[10] Ці інваріанти підтримують злиття як приблизно збалансовані.

Злиття додатково необхідної пам'яті

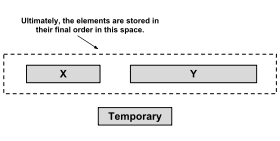
Щоб об'єднати набори, Timsort копіює елементи меншого масиву (X на цій ілюстрації) у тимчасову пам'ять, потім сортує та заповнює елементи в остаточному порядку в об'єднаний простір X та Y.

Початкова реалізація сортування злиттям не виконується без використання додаткового простору, тобто використовує N (розмір даних). Реалізації сортування об'єднаннями без використання додаткової пам'яті існують, але мають великі витрати часу. Timsort натомість виконує сортування з меншими витратами часу, використовуючи невеликий додатковий простір(<N)(щоб досягти середнього значення).

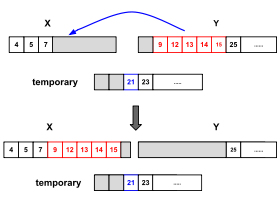
По-перше, Timsort виконує двійковий пошук, щоб знайти місце, куди перший елемент другого набору буде вставлений у першому впорядкованому наборі, зберігаючи його впорядкованим. Потім він виконує той самий алгоритм, щоб знайти місце, куди буде вставлено останній елемент першого набору у другому впорядкованому наборі, зберігаючи його впорядкованим. Елементи до та після цих розташувань уже на своїх правильних місцях і їх не потрібно об'єднувати. Потім менший із решти елементів двох наборів копіюється у тимчасову пам'ять, а елементи об'єднуються з більшим набором, звільняючи простір. Якщо перший набір менший, злиття починається з початку; якщо другий менший, злиття починається в кінці. Ця оптимізація зменшує кількість необхідних переміщень елементів, час роботи та тимчасові накладні витрати пам'яті в загальному випадку.

Приклад: два набори [1, 2, 3, 6, 10] та [4, 5, 7, 9, 12, 14, 17] повинні бути об'єднані. Зауважте, що вони вже відсортовані окремо. Найменший елемент другого набору - 4, і його слід додати на четвертій позиції першого набору, щоб зберегти його порядок (припускаючи, що перша позиція набору дорівнює 1). Найбільший елемент першого набору - 10, і його слід додати на п'ятій позиції другого набору, щоб зберегти його порядок. Тому [1, 2, 3] та [12, 14, 17] вже знаходяться у своїх остаточних положеннях, а набори, в яких потрібні переміщення елементів, - [6, 10] та [4, 5, 7, 9]. Маючи ці знання, нам потрібно лише виділити тимчасовий буфер розміром 2 замість 5.

Напрямок об'єднання

Об'єднання можна здійснювати в обох напрямках: зліва направо, як у традиційному сортуванні, або справа наліво.

Режим галопування під час злиття

Елементи (на які вказує синя стрілка) порівнюють, а менший елемент переміщують у кінцеве положення (на яке вказує червона стрілка).

Індивідуальне злиття наборів R1 та R2 зберігає кількість послідовних елементів, вибраних із циклу. Коли це число досягає мінімального порогу галопу (min_gallop), Timsort вважає, що ймовірно, що багато послідовних елементів все ще можуть бути вибрані з цього запуску, і перемикається в режим галопу. Припустимо, що R1 відповідає за його запуск. У цьому режимі алгоритм виконує експоненціальний пошук, також відомий як галопуючий пошук, для наступного елемента x циклу R2 у прогоні R1. Це робиться у два етапи: перший знаходить діапазон (2 k — 1, 2 k+1 — 1) де x. Другий етап виконує двійковий пошук елемента x у діапазоні, знайденому на першому етапі. Режим галопу — це спроба адаптувати алгоритм злиття до шаблону інтервалів між елементами в наборів.

Усі червоні елементи менші за сині (тут, 21). Таким чином, вони можуть бути переміщені фрагментом до остаточного масиву.

Галоп не завжди ефективний. У деяких випадках режим галопу вимагає більше порівнянь, ніж простий лінійний пошук . Відповідно до орієнтирів, розроблених розробником, галоп вигідний лише тоді, коли початковий елемент одного пробігу не є одним із перших семи елементів іншого прогону. Це передбачає початковий поріг 7. Щоб уникнути недоліків режиму галопування, виконуються дві дії: (1) Якщо галопування виявляється менш ефективним, ніж бінарний пошук, режим галопу виходить. (2) Успіх або невдача галопу використовується для коригування min_gallop . Якщо вибраний елемент з того самого масиву, який повертав елемент раніше, min_gallop зменшується на одиницю, таким чином заохочуючи повернення до режиму галопу. В іншому випадку значення збільшується на одиницю, тим самим перешкоджаючи поверненню в режим галопу. У разі випадкових даних значення min_gallop стає настільки великим, що режим галопу ніколи не повторюється.[11]

Низхідні набори

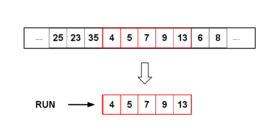
Для того, щоб також скористатися даними, відсортованими в порядку спадання, Timsort обертає строго низхідні набори, коли їх знаходить, і додає до стеку наборів. Оскільки низхідні набори пізніше сліпо змінюються, виключення наборів з рівними елементами підтримує стабільність алгоритму; тобто рівні елементи не буде змінено.

Мінімальний розмір набору

Алгоритм Timsort шукає впорядковані послідовності мінімального розміру(minruns), для виконання їх сортування.

Оскільки злиття є найбільш ефективним, коли кількість наборів дорівнює або трохи менша за потужність двох, і особливо менш ефективним, коли кількість наборів трохи більше, ніж потужність двох, Timsort вибирає minrun, щоб спробувати забезпечити колишній стан.

Minrun вибирається з діапазону від 32 до 64 включно, таким чином, що розмір даних, поділений на minrun, дорівнює або трохи менший за потужність двох. Остаточний алгоритм бере шість найбільш значущих бітів розміру масиву, додає один, якщо будь -який з решти бітів встановлено, і використовує цей результат як minrun. Цей алгоритм працює для всіх масивів, включаючи ті, що менші за 64; для масивів розміром 63 або менше це встановлює minrun рівним розміру масиву, а Timsort зменшує до сортування вставки.

Аналіз

У гіршому випадку, Timsort бере порівняння для сортування масиву з n елементів. У кращому випадку, що відбувається, коли вхідні дані вже відсортовані, він працює за лінійний час, що означає, що це адаптивний алгоритм сортування. [3]

Це переваги перед Quicksort для сортування посилань на об'єкти або покажчиків, оскільки вони вимагають дорогої непрямої пам'яті для доступу до даних та виконання порівнянь, а переваги когерентності кешу Quicksort значно зменшуються.

Офіційна перевірка

У 2015 році нідерландські та німецькі дослідники в рамках проекту FP7 ENVISAGE ЄС виявили помилку у стандартній реалізації Timsort.[12]

Зокрема, інваріанти розмірів набору, що складаються між собою, забезпечують чітку верхню межу максимального розміру необхідного стека. Реалізація заздалегідь виділила стек, достатній для сортування 2 64 байт введення, і уникнула подальших перевірок переповнення.

Однак гарантія вимагає, щоб інваріанти застосовувалися до кожної групи з трьох послідовних наборів, але реалізація перевірила це лише на трійку найкращих.[12] Використовуючи інструмент KeY для офіційної перевірки програмного забезпечення Java, дослідники виявили, що цієї перевірки недостатньо, і їм вдалося знайти довжини виконання (і вхідні дані, які генерували ці довжини виконання), що призведе до порушення інваріантів глибше в стеку після злиття вершини стека.[13]

Як наслідок, для певних входів виділеного розміру недостатньо для утримання всіх об'єднаних наборів. У Java це генерує для цих входів виняток, що виходять за межі масиву. Найменший вхід, який викликає цей виняток у Java та Android v7, має розмір 67108864 (2 26). (Старіші версії Android вже викликали цей виняток для певних вхідних даних розміром 65536 (2 16))

Реалізацію Java було виправлено шляхом збільшення розміру попередньо виділеного стека на основі оновленого аналізу найгіршого випадку. Стаття також формальними методами показала, як встановити передбачуваний інваріант, перевіривши, чи чотири верхніх прогону в стеку відповідають двом вищезазначеним правилам. Цей підхід був прийнятий Python[14] та Android.

Примітки

  1. ↑ Peters, Tim. [Python-Dev] Sorting. Python Developers Mailinglist. Процитовано 24 лютого 2011. [Timsort] also has good aspects: It's stable (items that compare equal retain their relative order, so, e.g., if you sort first on zip code, and a second time on name, people with the same name still appear in order of increasing zip code; this is important in apps that, e.g., refine the results of queries based on user input). ... It has no bad cases (O(N log N) is worst case; N−1 compares is best).
  2. ↑ [DROPS]. Процитовано 1 вересня 2018. TimSort is an intriguing sorting algorithm designed in 2002 for Python, whose worst-case complexity was announced, but not proved until our recent preprint.
  3. ↑ а б Chandramouli, Badrish; Goldstein, Jonathan (2014). Patience is a Virtue: Revisiting Merge and Sort on Modern Processors. SIGMOD/PODS.
  4. ↑ [#JDK-6804124] (coll) Replace "modified mergesort" in java.util.Arrays.sort with timsort. JDK Bug System. Процитовано 11 червня 2014.
  5. ↑ Class: java.util.TimSort<T>. Android Gingerbread Documentation. Архів оригіналу за 16 July 2015. Процитовано 24 February 2011.
  6. ↑ liboctave/util/oct-sort.cc. Mercurial repository of Octave source code. Lines 23-25 of the initial comment block. Процитовано 18 February 2013. Code stolen in large part from Python's, listobject.c, which itself had no license header. However, thanks to Tim Peters for the parts of the code I ripped-off.
  7. ↑ Is sort() stable in Swift 5?. Swift Forums (амер.). 4 липня 2019. Процитовано 4 липня 2019.
  8. ↑ slice - Rust. doc.rust-lang.org. Процитовано 17 вересня 2020. The current algorithm is an adaptive, iterative merge sort inspired by timsort. It is designed to be very fast in cases where the slice is nearly sorted, or consists of two or more sorted sequences concatenated one after another.
  9. ↑ McIlroy, Peter (January 1993). Optimistic Sorting and Information Theoretic Complexity. Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms. с. 467—474. ISBN 0-89871-313-7.
  10. ↑ MacIver, David R. (11 січня 2010). Understanding timsort, Part 1: Adaptive Mergesort. Процитовано 5 грудня 2015.
  11. ↑ Peters, Tim. listsort.txt. CPython git repository. Процитовано 5 грудня 2019.
  12. ↑ а б de Gouw, Stijn; Rot, Jurriaan; de Boer, Frank S.; Bubel, Richard; Hähnle, Reiner (July 2015). OpenJDK's Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst Case (PDF). Computer Aided Verification: 273—289. doi:10.1007/978-3-319-21690-4_16.
  13. ↑ de Gouw, Stijn (24 лютого 2015). Proving that Android’s, Java’s and Python’s sorting algorithm is broken (and showing how to fix it). Процитовано 6 травня 2017.
  14. ↑ Python Issue Tracker — Issue 23515: Bad logic in timsort's merge_collapse

Рекомендована література

Посилання

  • timsort.txt — оригінальне пояснення Тіма Пітерса
Отримано з https://uk.wikipedia.org/w/index.php?title=Timsort&oldid=34595282