Перетворення Бокса-Мюллера

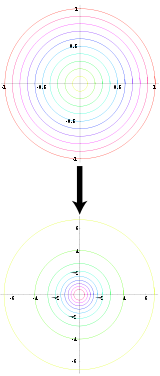
Перетвóрення Боксу — Мюллера — метод моделювання стандартних нормально розподілених випадкових величин. Має два варіанти. Метод є точним, на відміну, наприклад, від методів що ґрунтуються на центральній граничній теоремі.

Метод був опублікований в 1958 році Джорджем Боксом і Мервіном Мюллером.

Перший варіант

Нехай $r$ і $\phi$  — незалежні випадкові величини, рівномірно розподілені на інтервалі $(0,1]$. Обчислимо $z_{0}$ і $z_{1}$ за формулами:

$z_{0}=\cos(2\pi \phi ){\sqrt {-2\ln r}},$

$z_{1}=\sin(2\pi \phi ){\sqrt {-2\ln r}}.$

Тоді $z_{0}$ і $z_{1}$ будуть незалежні і розподілені нормально з математичним сподіванням 0 і дисперсією 1. При реалізації на комп'ютері зазвичай швидше не обчислювати обидві тригонометричні функції — $\cos(\cdot )$ і $\sin(\cdot )$ — а розрахувати одну з них через іншу. Ще краще скористатися натомість другим варіантом перетворення Боксу — Мюллера.

Другий варіант

Нехай $x$ і $y$  — незалежні випадкові величини, рівномірно розподілені на відрізку $[-1,1]$. Обчислимо $R=x^{2}+y^{2}$. Якщо виявиться, що $R>1$ чи $R=0$, то значення $x$ і $y$ слід «викинути» і згенерувати наново. Як тільки виконається умова $0<R\leq 1$ за формулами

$z_{0}=x\cdot {\sqrt {-2\ln R \over R}}$

і

$z_{1}=y\cdot {\sqrt {-2\ln R \over R}}$

слід розрахувати $z_{0}$ и $z_{1}$, які, як і в першому випадку, будуть незалежними величинами, що задовольняють стандартному нормальному розподілу.

Коефіцієнт використовування базових випадкових величин для першого варіанту, очевидно, дорівнює одиниці. Для другого варіанту це відношення площі кола одиничного радіусу до площі квадрата із стороною два, тобто $\pi /4\approx 0,785$. Проте, на практиці другий варіант зазвичай виявляється швидшим, за рахунок того, що в ньому використовується тільки одна трансцендентна функція $\ln(\cdot )$. Ця перевага для більшості реалізацій переважує необхідність генерації більшого числа рівномірно розподілених випадкових величин.

Перехід до загального нормального розподілу

Після отримання стандартної нормальної випадкової величини $z$, можна легко перейти до величини $\xi \sim N(\mu ,\sigma ^{2})$, що є нормально розподіленою з математичним очікуванням $\mu$ і стандартним відхиленням $\sigma$ за формулою:

$\xi =\mu +\sigma z.$

Це вже не є частиною перетворення Боксу — Мюллера, але дозволяє завершити генерацію нормальної випадкової величини.

Реалізація

Приклад реалізації на мові C# генерації нормально розподілених випадкових величин за допомогою другого варіанту перетворення.

//Об'єкт для генерації рівномірно-розподіленої величини
Random RND = new Random();
//Ця змінна зберігає друге прогенероване ще не використане значення, для прискорення послідовної генерації багатьох значень
double LastFreeValue = double.NaN;

/// <summary>
/// Нормально розподілена випадкова величина
/// </summary>
double RNDGauss_BoxMuller()
    {
        if(double.IsNaN(LastFreeValue))
        {
            //якщо невикористаного значення немає - генерується наступна пара
            double x = 0, y = 0, R = 2;
            while (R > 1)
            {
                //генеруються випадкові x та y, поки не буде виконана умова R <= 1
                x = RND.NextDouble() * 2 - 1;
                y = RND.NextDouble() * 2 - 1;
                R = x * x + y * y;
            }
            double t = Math.Sqrt(-2 * Math.Log(R) / R);
            //друге випадкове значення зберігається для подальшого використання
            LastFreeValue = y * t;
            //повертається перше прогенероване випадкове значення
            return x * t;
        }
        else
        {
            //якщо є невикористане значення - воно повертається і обнуляється
            double Z1 = LastFreeValue;
            LastFreeValue = double.NaN;
            return Z1;
        }
    }