Нормальний розподіл

Нормальний розподіл
	Щільність розподілу; ; Червона лінія — стандартний нормальний розподіл.
	Функція розподілу ймовірностей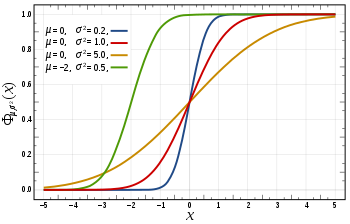; ; Кольори такі ж як і на попередньому малюнку.
Параметри	μ параметр знаходження (дійсне); σ2 > 0 квадрат параметру масштабу (дійсне)
Сапорт
Розподіл ймовірностей
Функція розподілу ймовірностей (cdf)
Середнє	μ
Медіана	μ
Мода	μ
Дисперсія	σ2
Коефіцієнт асиметрії	0
Коефіцієнт ексцесу	0
Ентропія
Твірна функція моментів (mgf)
Характеристична функція

Матеріал з Вікіпедії — вільної енциклопедії.

Перейти до: навігація, пошук

Нормальний розподіл

Нормальний розподіл (розподіл Ґаусса) — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності

$f(x;\mu;\sigma) = \frac{1}{\sigma\sqrt{2\pi}} \, \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right)$

де $μ$ — математичне сподівання, $σ 2$ — дисперсія випадкової величини.

Нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль. Наприклад, відстань від влучення снаряду гармати до цілі при великій кількості пострілів характеризується саме нормальним розподілом.

[ред.] Дивіться також

У Вікіпедії є портал

«Математика»

Це незавершена стаття з математики.
Ви можете допомогти проекту, виправивши або дописавши її.

Нормальний розподіл

Матеріал з Вікіпедії — вільної енциклопедії.

[ред.] Дивіться також

Перегляди

Особисті інструменти

Навігація

Участь

Пошук

Панель інструментів

Іншими мовами

Щільність розподілу Червона лінія — стандартний нормальний розподіл.
Функція розподілу ймовірностей Кольори такі ж як і на попередньому малюнку.
Параметри	$μ$ параметр знаходження (дійсне) $σ 2 > 0$ квадрат параметру масштабу (дійсне)
Сапорт	$x \in\mathbb{R}\!$
Розподіл ймовірностей	$\frac{1}{\sigma \sqrt{2\pi} } \exp \left(-\frac{(x-\mu)^2}{2\sigma ^2} \right)$
Функція розподілу ймовірностей (cdf)	$\frac12 \left(1+\mathrm{erf}\left( \frac{x-\mu}{\sigma\sqrt2}\right) \right)$
Середнє	$μ$
Медіана	$μ$
Мода	$μ$
Дисперсія	$σ 2$
Коефіцієнт асиметрії	0
Коефіцієнт ексцесу	0
Ентропія	$\ln\left(\sigma\sqrt{2\,\pi\,e}\right)\!$
Твірна функція моментів (mgf)	$M_X(t)= \exp\left(\mu\,t+\frac{\sigma^2 t^2}{2}\right)$
Характеристична функція	$\chi_X(t)=\exp\left(\mu\,i\,t-\frac{\sigma^2 t^2}{2}\right)$