Гіперболічні функції

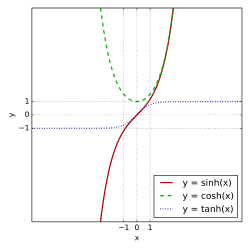
sinh, cosh та tanh

Гіперболі́чні фу́нкції — сімейство елементарних функцій, які виражаються через експоненту і тісно пов'язанні з тригонометричними функціями.

Визначення

Визначення гіперболічних функцій через гіперболу

Один із способів визначення тригономітричних функцій через одиничне коло

Гіперболічні функції задаються такими формулами:

• гіперболічний синус:

$\mathop{\mathrm{sh}}\,x=\frac{e^x-e^{-x}}{2}$ (в іноземній літературі позначається $\sinh x$)

Існує сленгова назва: «шинус», «шимус»(?).

• гіперболічний косинус:

$\mathop{\mathrm{ch}}\,x=\frac{e^x+e^{-x}}{2}$ (в іноземній літературі позначається $\cosh x$)

Існує сленгова назва: «чосинус», «кошинус». Лінію гіперболічного косинусу називають ланцюговою, бо саме таку форму приймає ланцюг або мотузка, що підвисили за обидва кінці в однорідному гравітаційному полі.

• гіперболічний тангенс:

$\mathop{\mathrm{th}}\,x=\frac{\mathop{\mathrm{sh}}\,x}{\mathop{\mathrm{ch}}\,x}$ (в іноземній літературі позначається $\tanh x$).

Існує сленгова назва: «щангенс».

Іноді також визначається

• гіперболічний котангенс:

$\mathop{\mathrm{cth}}\,x=\frac{1}{\mathop{\mathrm{th}}\,x}$,

• гіперболічні секанс і косеканс:

$\mathop{\mathrm{sch}}\,x=\frac{1}{\mathop{\mathrm{ch}}\,x}$,

$\mathop{\mathrm{csch}}\,x=\frac{1}{\mathop{\mathrm{sh}}\,x}$.

Властивості

Зв'язок з тригонометричними функціями

Гіперболічні функції виражаються через тригонометричні функції від уявного аргументу.

$\operatorname{sh}x=-i\sin(ix),\quad \operatorname{ch}x=\cos(ix),\quad \operatorname{th}x=-i\operatorname{tg}(ix)$.

$\operatorname{sh}(ix) = i\operatorname{sin}x,\quad \operatorname{ch}(ix) = \cos x,\quad \operatorname{th}(ix)= i\operatorname{tg}x$.

Функція Гудермана зв'язує тригонометричні функції і гіперболічні функції без залучення комплексних чисел.

Важлива тотожність

1. $\operatorname{ch}^2x-\operatorname{sh}^2x=1$
2. Парність:
   1. $\operatorname{sh}(-x)=-\operatorname{sh} x$
   2. $\operatorname{ch}(-x)=\operatorname{ch} x$
   3. $\operatorname{th}(-x)=-\operatorname{th} x$
3. Формули додавання:
   1. $\operatorname{sh}(x \pm y)=\operatorname{sh}x\,\operatorname{ch}y \pm \operatorname{sh}y\,\operatorname{ch}x$
   2. $\operatorname{ch}(x \pm y)=\operatorname{ch}x\,\operatorname{ch}y \pm \operatorname{sh}y\,\operatorname{sh}x$
   3. $\operatorname{th}(x \pm y)=\frac{\operatorname{th}x \pm \operatorname{th}y}{1 \pm \operatorname{th}x\operatorname{th}y}$
4. Формули подвоєного кута:
   1. $\operatorname{sh}2x=2\operatorname{ch}x\,\operatorname{sh}x=\frac{2\,\operatorname{th}x}{1-\operatorname{th}^2x}$
   2. $\operatorname{ch}2x=\operatorname{ch}^2x+\operatorname{sh}^2x=2\operatorname{ch}^2x-1=1+2\operatorname{sh}^2x=\frac{1+\operatorname{th}^2x}{1-\operatorname{th}^2x}$
   3. $\operatorname{th}2x=\frac{2\operatorname{th}x}{1+\operatorname{th}^2x}$
   4. $\operatorname{cth}2x=\frac{1}{2} (\operatorname{th}x+\operatorname{cth}x)$
   5. $\operatorname{th}x=\frac{\operatorname{ch}2x-1}{\operatorname{sh}2x}=\frac{\operatorname{sh}2x}{1+\operatorname{ch}2x}$
   6. $\operatorname{ch}2x \pm \operatorname{sh}2x=(\operatorname{sh}x\pm\operatorname{ch}x)^2$
5. Формули кратних кутів:
   1. $\operatorname{sh}3x=4\operatorname{sh}^3x+3\operatorname{sh}x$
   2. $\operatorname{ch}3x=4\operatorname{ch}^3x-3\operatorname{ch}x$
   3. $\operatorname{th}3x=\operatorname{th}x\frac{3+\operatorname{th}^2x}{1+3\operatorname{th}^2x}$
   4. $\operatorname{sh}5x=16\operatorname{sh}^5x+20\operatorname{sh}^3x+5\operatorname{sh}x$
   5. $\operatorname{ch}5x=16\operatorname{ch}^5x-20\operatorname{ch}^3x+5\operatorname{ch}x$
   6. $\operatorname{th}5x=\operatorname{th}x\frac{\operatorname{th}^4x+10\operatorname{th}^2x+5}{5\operatorname{th}^4x+10\operatorname{th}^2x+1}$
6. Добуток
   1. $\operatorname{sh}x\operatorname{sh}y=\frac{\operatorname{ch}(x+y)-\operatorname{ch}(x-y)}{2}$
   2. $\operatorname{sh}x\operatorname{ch}y=\frac{\operatorname{sh}(x+y)+\operatorname{sh}(x-y)}{2}$
   3. $\operatorname{ch}x\operatorname{ch}y=\frac{\operatorname{ch}(x+y)+\operatorname{ch}(x-y)}{2}$
   4. $\operatorname{th}x\operatorname{th}y=\frac{\operatorname{ch}(x+y)-\operatorname{ch}(x-y)}{\operatorname{ch}(x+y)+\operatorname{ch}(x-y)}$
7. Суми
   1. $\operatorname{sh}x \pm \operatorname{sh}y=2\operatorname{sh}\frac{x \pm y}{2}\operatorname{ch}\frac{x \mp y}{2}$
   2. $\operatorname{ch}x + \operatorname{ch}y=2\operatorname{ch}\frac{x+y}{2}\operatorname{ch}\frac{x -y}{2}$
   3. $\operatorname{ch}x - \operatorname{ch}y=2\operatorname{sh}\frac{x+y}{2}\operatorname{sh}\frac{x -y}{2}$
   4. $\operatorname{th}x \pm \operatorname{th}y=\frac{\operatorname{sh}x \pm y}{\operatorname{ch}x\operatorname{ch}y}$
8. Формули пониження степеня
   1. $\operatorname{ch}^2\frac{x}{2} = \frac{\operatorname{ch} x + 1}{2}$
   2. $\operatorname{sh}^2\frac{x}{2} = \frac{\operatorname{ch} x - 1}{2}$
9. Похідні:
   1. $(\operatorname{sh}x)^\prime=\operatorname{ch}x$
   2. $(\operatorname{ch}x)^\prime=\operatorname{sh}x$
   3. $(\operatorname{th}x)^\prime=\frac{1}{\operatorname{ch}^2x}$
   4. $\operatorname{sh}x=\int\limits^x_0\operatorname{ch}tdt$
   5. $\operatorname{ch}x=1+\int\limits^x_0\operatorname{sh}tdt$
   6. $\operatorname{th}x=\int\limits^x_0\frac{dt}{\operatorname{ch}^2t}$
10. Інтеграли:
    1. $\int\operatorname{sh}x\,dx=\operatorname{ch}x+C$
    2. $\int\operatorname{ch}x\,dx=\operatorname{sh}x+C$
    3. $\int\operatorname{th}x\,dx=\ln\operatorname{ch}x+C$
    4. $\int\frac{1}{\operatorname{ch}^2x}\,dx=\operatorname{th}x+C$
    5. $\int\frac{1}{\operatorname{sh}^2x}\,dx=-\operatorname{cth}x+C$

Дивись також: Таблиця інтегралів гіперболічних функцій, Таблиця інтегралів обернених гіперболічних функцій

Нерівності

При всіх $x\in\mathbb{R}$ виконується:

1. $0 \le \operatorname{ch}x-1 \le |\operatorname{sh} x| < \operatorname{ch}x$
2. $| \operatorname{th}x | <1$

Розкладання в степенні ряди

$\operatorname{sh}x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\frac{x^7}{7!}+\ldots=\sum_{n=0}^\infty\frac{x^{2n+1}}{(2n+1)!}$

$\operatorname{ch}x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\ldots=\sum_{n=0}^\infty\frac{x^{2n}}{(2n)!}$

$\operatorname{th}x=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\ldots=\sum_{n=1}^\infty\frac{(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!},\quad|x|<\frac{\pi}{2}$

$\operatorname{cth}x=\frac{1}{x}+\frac{x}{3}-\frac{x^3}{45}+\frac{2x^5}{945}+\ldots=\frac{1}{x}+\sum_{n=1}^\infty\frac{(-1)^{n-1}2^{2n}B_{2n}x^{2n-1}}{(2n)!},\quad0<|x|<\pi$ (Ряд Лорана)

Тут $B_{2n}$ — числа Бернуллі.

Графіки

sh(x), ch(x), th(x), cth(x)

Аналітичні властивості

Гіперболічний синус і гіперболічний косинус аналітичний у всій комплексній площині, за винятком істотно особливої точки на нескінченності. Гіперболічний тангенс аналітичний скрізь, окрім полюсів в точках $z=i\pi(n+1/2)$, де $n$ — ціле. Вирахування у всіх цих полюсах рівні одиниці. Гіперболічний котангенс аналітичний скрізь, окрім точок $z=i\pi n$, вирахування його в цих полюсах також рівні одиниці.

Див. також

• Обернені гіперболічні функції