Ланцюгова лінія
| Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. (лютий 2020) |

Ланцюгова лінія, чи катена́рія (лат. catenaria, від catēna — «ланцюг») — лінія, форму якої набуває гнучка однорідна нерозтяжна важка нитка або ланцюг (звідси назва) із закріпленими кінцями в однорідному гравітаційному полі. Вона є плоскою трансцендентною кривою. Рівняння в прямокутних координатах:
Властивості[ред. | ред. код]
- Крива є симетричною відносно осі ординат.
- Довжина дуги , де , дорівнюєде — гіперболічний синус.
- Проєкція ординати довільної точки ланцюгової лінії на нормаль у цій точці є сталою величиною і дорівнює .
- Радіус кривини ланцюгової лінії в будь-якій її точці можна обчислити за формулою: .
- Площа фігури, обмеженої ланцюговою лінією, заданою на проміжку і віссю абсцис, дорівнює .
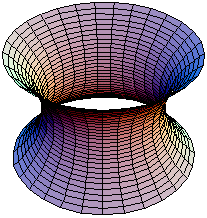
- Якщо дугу ланцюгової лінії обертати навколо осі , то утвориться поверхня обертання, яка називається катеноїдом.
Історичні відомості[ред. | ред. код]
Протягом сторіч відомі вчені досліджували ланцюгову лінію, знаходили певні закономірності, досліджували їх властивості. На сьогодні нам вже відомо безліч можливостей її застосування.
У книзі Галілея «Бесіди і математичні докази …» (1638 р) було запропоновано наступний спосіб побудови параболи:
"Заб'ємо в стіну два цвяха на однаковій висоті над горизонтом і на такій відстані один від одного, щоб вона дорівнювала подвійній ширині прямокутника, на якому можна побудувати одну гілку параболи; між цвяхами підвісимо тонкий ланцюжок, який звішувався б вниз і був такої довжини, щоб найнижча його точка знаходилася від рівня цвяха на відстані, рівному висоті прямокутника. Цей ланцюжок, звисаючи, розташується у вигляді параболи, так що, відзначивши її слід на стіні пунктиром, ми отримаємо параболу, яку навпіл розсікає перпендикуляр, проведений через середину лінії, що з'єднує обидва цвяха".
Спосіб цей простий і наочний, але не точний. Це розумів і сам Галілей. Насправді, якщо параболу побудувати за всіма правилами, то між нею і ланцюжком виявляться щілини. Тільки через півстоліття після виходу книги Галілея старший з двох братів-математиків Бернуллі Якоб знайшов теоретичним шляхом точну формулу провисаючого ланцюжка. Не поспішаючи повідомляти своє рішення задачі, він кинув виклик іншим математикам. Правильне рішення вже в наступному 1691 р. опублікували Християн Гюйгенс, Ґотфрід Ляйбніц і молодший брат Якоба Йоганн Бернуллі. Всі вони користувалися для вирішення завдання, по-перше, законами механіки, а по-друге, могутніми засобами нещодавно розробленого тоді математичного аналізу — диференціюванням та інтегруванням. Саме Гюйгенс запропонував термін Ланцюгова лінія (catenary) (1690) (лат. catenary — ланцюг; англ. chain).
Отримання формули[ред. | ред. код]

Розглянемо сили, які діють на ланцюг. Нехай
- — це нижня точка ланцюга.
- — деяка довільна точка ланцюга.
- — довжина дуги кривої.
- — лінійна густина ланцюга.
Дуга знаходиться у рівновазі. На неї діють три сили:
- — напруження в точці ;
- — напруження в точці ;
- — вага ділянки .
Сила напруження діє по дотичній в точках та . Можемо записати наступні рівняння:
та
- .
Поділемо ці рівняння і отримаємо:
де . Але дорівнює похідній в точці . Отже,
Продиференціюємо це рівняння по .
Застосуємо відому формулу диференціала дуги: і отримаємо диференціальне рівняння другого порядку:
Зробимо заміну: Тоді
і проінтегруємо
Ліворуч:
Праворуч:
Отже,
Для ми маємо , отже і
- ,
звідки
Далі
- .
Отже,
і
- .
Візьмемо . А також замінемо на . Остаточно маємо:
і нижня точка має координати
Застосування ланцюгової лінії[ред. | ред. код]

Застосування в техніці[ред. | ред. код]
В області техніки ланцюгова лінія використовується в розрахунках, пов'язаних з провисанням ниток — проводів, тросів і т. д.
При виведенні рівняння ланцюгової лінії зазначається, що , де — натяг нитки в вершині, а — питома щільність матеріалу, з якого зроблена нитка. Далі, горизонтальна складова сили натягу в довільній точці ланцюгової лінії визначалася виразом , і з огляду на те, що нитка знаходилась в рівновазі, була отримана рівність . Виключаємо параметр з цієї рівності та попередньої, отримуємо
Говорячи про застосування ланцюгової лінії в техніці, варто згадати про так звані лінії склепінь, що має рівняння

Цю криву можна отримати афінним перетворенням звичайної ланцюгової лінії. Вона знаходить застосування в будівельній техніці при проектуванні склепінь.
Проектування арок та будівництво мостів[ред. | ред. код]
Ланцюгова лінія використовується в будівництві арок (оскільки форма арки у вигляді перевернутої ланцюгової лінії найбільш вдало розподіляє навантаження), при будуванні мостів, при розрахунках, пов'язаних із провисанням проводів, канатів (однорідний канат або ланцюг вільно підвішений за свої кінці, набуває форми графіка гіперболічного косинуса, який ще називають ланцюговою лінією).
Перевернута ланцюгова лінія — ідеальна форма для арок. Однорідна арка у формі перевернутої ланцюгової лінії відчуває тільки деформації стиску, але не зламу.
Форма ланцюгової лінії постійно змінюється під впливом різних випадкових і невипадкових факторів, тому теоретично складно виявити закономірність цієї зміни. Для відносно коротких робочих ланцюгів та невеликих провисань ланцюгову лінію можна замінити параболою.
На арці Саарінена в Сент-Луїсі написана її формула в футах :

У метрах це
«Горбатий» міст має форму, близьку до ланцюгової лінії.
Варто зауважити, що ланцюг підвісного моста має форму параболи, а не ланцюгової лінії. Це пов'язано з тим, що проліт мосту набагато важче ланцюга. Прикладом є знаменитий міст «Золота Брама» в Сан-Франциско.
Ланцюгові арки часто використовуються в будівництві печей. Щоб створити бажану криву, форму висячого ланцюга бажаних розмірів переносять на шаблон, який потім використовується як керівництво для розміщення цеглини або інших будівельних матеріалів.
Література[ред. | ред. код]
- Атанасян Л. С., Базылев В. Т. Геометрия. — учебное пособие для студентов физ. — мат. факультетов пед. институтов. — М.: Просвещение, 1987.
- Гильберт Д., Кон-Фостен С. Наглядная геометрия. — М.: Наука, 1981.
- Люстерник Л. А. Кратчайшие линии. Вариационные задачи. Серия «Популярные лекции по математике», выпуск 19, § 19. М.-Л.: Гостехиздат, 1955.
- Математическая энциклопедия. В пяти томах. Том 5./ Под ред. И. М. Виноградова. М.: Советская энциклопедия, 1984.
- Моденов П. С. Аналитическая геометрия М.: Наука, 1969.
- Працьовитий М. В., Гончаренко Я. В. Лінії на евклідовій площині. — К.: НПУ імені М. П. Драгоманова, 2005. — 44 с.
- Савелов А. А. Плоские кривые. М., 1960—293с.
| Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


























































