Ортогональні поліноми
Чебишова
Відкриті
Пафнутієм Чебишовим у 1854 році
Формула
T
n
(
x
)
=
(
x
+
x
2
−
1
)
n
+
(
x
−
x
2
−
1
)
n
2
{\displaystyle T_{n}(x)={\frac {(x+{\sqrt {x^{2}-1}})^{n}+(x-{\sqrt {x^{2}-1}})^{n}}{2}}}
U
n
(
x
)
=
(
x
+
x
2
−
1
)
n
+
1
−
(
x
−
x
2
−
1
)
n
+
1
2
x
2
−
1
{\displaystyle U_{n}(x)={\frac {(x+{\sqrt {x^{2}-1}})^{n+1}-(x-{\sqrt {x^{2}-1}})^{n+1}}{2{\sqrt {x^{2}-1}}}}}
Диференціальне рівняння
(
1
−
x
2
)
y
″
−
x
y
′
+
n
2
y
=
0
{\displaystyle (1-x^{2})\,y''-x\,y'+n^{2}\,y=0\,\!}
i
(
1
−
x
2
)
y
″
−
3
x
y
′
+
n
(
n
+
2
)
y
=
0
{\displaystyle (1-x^{2})\,y''-3x\,y'+n(n+2)\,y=0\,\!}
Визначені на
[
−
1
,
1
]
{\displaystyle \ [-1,1]}
Вага
1
1
−
x
2
{\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}}
1
−
x
2
{\displaystyle {\sqrt {1-x^{2}}}}
Норма
{
π
:
n
=
0
π
/
2
:
n
≠
0
{\displaystyle {\begin{cases}\pi &:n=0\\\pi /2&:n\neq 0\end{cases}}}
π
/
2
{\displaystyle \pi /2\;}
Примітки
Нулі поліномів Чебишова першого роду є оптимальними вузлами інтерполяційних схем .
Поліноми Чебишева — дві послідовності поліномів
{
T
n
(
x
)
}
n
=
0
∞
{\displaystyle \{T_{n}(x)\}_{n=0}^{\infty }}
{
U
n
(
x
)
}
n
=
0
∞
{\displaystyle \{U_{n}(x)\}_{n=0}^{\infty }}
Пафнутія Чебишова .
Поліном Чебишова першого роду визначається як
T
0
=
1
,
T
n
(
x
)
=
cos
(
n
arccos
x
)
,
{\displaystyle T_{0}=1,\quad \quad T_{n}(x)=\cos(n\arccos x),}
де
n
=
1
,
2
,
3
,
.
.
.
{\displaystyle n=1,2,3,...}
T
n
(
x
)
{\displaystyle T_{n}(x)}
n
{\displaystyle n}
2
n
−
1
{\displaystyle 2^{n-1}}
[
−
1
,
1
]
{\displaystyle [-1,1]}
w
(
x
)
=
1
/
(
1
−
x
2
)
1
/
2
{\displaystyle w(x)=1/(1-x^{2})^{1/2}}
[
−
1
,
1
]
{\displaystyle [-1,1]}
θ
=
arccos
x
{\displaystyle \theta =\arccos x}
∫
−
1
+
1
T
n
(
x
)
T
m
(
x
)
d
x
(
1
−
x
2
)
1
/
2
=
∫
0
π
cos
n
θ
cos
m
θ
d
θ
=
0
(
m
≠
n
)
.
{\displaystyle \int _{-1}^{+1}T_{n}(x)T_{m}(x){\frac {dx}{(1-x^{2})^{1/2}}}=\int _{0}^{\pi }\cos n\theta \cos m\theta \,d\theta =0\quad \quad (m\neq n).}
Поліноми Чебишова другого роду визначаються як
U
0
=
1
,
U
n
(
x
)
=
sin
(
n
arccos
x
)
,
{\displaystyle U_{0}=1,\quad \quad U_{n}(x)=\sin(n\arccos x),}
де
n
=
1
,
2
,
3
,
.
.
.
{\displaystyle n=1,2,3,...}
U
n
(
x
)
{\displaystyle U_{n}(x)}
n
{\displaystyle n}
2
n
{\displaystyle 2^{n}}
інтеграл від абсолютної величини якого на проміжку
[
−
1
,
1
]
{\displaystyle [-1,1]}
Поліноми Чебишова можна записати у вигляді
T
n
(
x
)
=
1
/
2
[
(
x
+
i
1
−
x
2
)
n
+
(
x
−
i
1
−
x
2
)
n
]
,
{\displaystyle T_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}+(x-i{\sqrt {1-x^{2}}})^{n}],}
U
n
(
x
)
=
1
/
2
[
(
x
+
i
1
−
x
2
)
n
−
(
x
−
i
1
−
x
2
)
n
]
.
{\displaystyle U_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}-(x-i{\sqrt {1-x^{2}}})^{n}].}
Ці формули можна отримати, якщо вважати
x
=
cos
θ
,
{\displaystyle x=\cos \theta ,}
тригонометричні функції у експониненційній формі й застосовуючи теорему Муавра та замінюючи після цього
cos
θ
{\displaystyle \cos \theta }
x
,
{\displaystyle x,}
sin
θ
{\displaystyle \sin \theta }
(
1
−
x
2
)
1
/
2
.
{\displaystyle (1-x^{2})^{1/2}.}
Бінономіальний розклад рівнянь
T
n
(
x
)
=
1
/
2
[
(
x
+
i
1
−
x
2
)
n
+
(
x
−
i
1
−
x
2
)
n
]
,
{\displaystyle T_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}+(x-i{\sqrt {1-x^{2}}})^{n}],}
U
n
(
x
)
=
1
/
2
[
(
x
+
i
1
−
x
2
)
n
−
(
x
−
i
1
−
x
2
)
n
]
{\displaystyle U_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}-(x-i{\sqrt {1-x^{2}}})^{n}]}
приводить до рівнянь, які можна використати для обчислення декількох поліномів Чебишева. Ці рівняння мають наступний вигляд
T
n
(
x
)
=
∑
r
=
0
n
/
2
(
−
1
)
r
n
!
(
2
r
)
!
(
n
−
2
r
)
!
(
1
−
x
2
)
r
x
n
−
2
r
,
{\displaystyle T_{n}(x)=\sum _{r=0}^{n/2}(-1)^{r}{\frac {n!}{(2r)!(n-2r)!}}(1-x^{2})^{r}x^{n-2r},}
U
n
(
x
)
=
∑
r
=
0
(
n
−
1
)
/
2
(
−
1
)
r
n
!
(
2
r
+
1
)
!
(
n
−
2
r
−
1
)
!
(
1
−
x
2
)
r
+
1
/
2
x
n
−
2
r
+
1
.
{\displaystyle U_{n}(x)=\sum _{r=0}^{(n-1)/2}(-1)^{r}{\frac {n!}{(2r+1)!(n-2r-1)!}}(1-x^{2})^{r+1/2}x^{n-2r+1}.}
Поліноми Чебишова першого роду
T
n
(
x
)
{\displaystyle T_{n}(x)}
T
0
(
x
)
=
1
{\displaystyle T_{0}(x)=1\,}
T
1
(
x
)
=
x
{\displaystyle T_{1}(x)=x\,}
T
2
(
x
)
=
2
x
2
−
1
,
{\displaystyle T_{2}(x)=2x^{2}-1,}
T
3
(
x
)
=
4
x
3
−
3
x
,
{\displaystyle T_{3}(x)=4x^{3}-3x,}
T
4
(
x
)
=
8
x
4
−
8
x
2
+
1
,
{\displaystyle T_{4}(x)=8x^{4}-8x^{2}+1,}
T
5
(
x
)
=
16
x
5
−
20
x
3
+
5
x
;
{\displaystyle T_{5}(x)=16x^{5}-20x^{3}+5x;}
T
n
+
1
(
x
)
=
2
x
T
n
(
x
)
−
T
n
−
1
(
x
)
.
{\displaystyle T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x).\,}
Поліноми Чебишова другого роду
U
n
(
x
)
{\displaystyle U_{n}(x)}
U
0
(
x
)
=
1
,
{\displaystyle U_{0}(x)=1,}
U
1
(
x
)
=
2
x
,
{\displaystyle U_{1}(x)=2x,}
U
2
(
x
)
=
(
1
−
x
2
)
1
/
2
,
{\displaystyle U_{2}(x)=(1-x^{2})^{1/2},}
U
2
(
x
)
=
(
1
−
x
2
)
1
/
2
2
x
,
{\displaystyle U_{2}(x)=(1-x^{2})^{1/2}2x,}
U
3
(
x
)
=
(
1
−
x
2
)
1
/
2
(
4
x
2
−
1
)
,
{\displaystyle U_{3}(x)=(1-x^{2})^{1/2}(4x^{2}-1),}
U
4
(
x
)
=
(
1
−
x
2
)
1
/
2
(
8
x
3
−
4
x
)
,
{\displaystyle U_{4}(x)=(1-x^{2})^{1/2}(8x^{3}-4x),}
U
5
(
x
)
=
(
1
−
x
2
)
1
/
2
(
16
x
4
−
12
x
2
+
1
)
.
{\displaystyle U_{5}(x)=(1-x^{2})^{1/2}(16x^{4}-12x^{2}+1).}
U
n
+
1
(
x
)
=
2
x
U
n
(
x
)
−
U
n
−
1
(
x
)
.
{\displaystyle U_{n+1}(x)=2xU_{n}(x)-U_{n-1}(x).\,}
Генератриса поліномів першого роду має вигляд:
∑
n
=
0
∞
T
n
(
x
)
t
n
=
1
−
t
x
1
−
2
t
x
+
t
2
.
{\displaystyle \sum _{n=0}^{\infty }T_{n}(x)t^{n}={\frac {1-tx}{1-2tx+t^{2}}}.\,\!}
Генератриса поліномів другого роду має вигляд:
∑
n
=
0
∞
U
n
(
x
)
t
n
=
1
1
−
2
t
x
+
t
2
.
{\displaystyle \sum _{n=0}^{\infty }U_{n}(x)t^{n}={\frac {1}{1-2tx+t^{2}}}.\,\!}
Поліноми Чебишова є розв'язками рівняння Пелля в кільці поліномів із дійсними коефіцієнтами:
T
n
(
x
)
2
−
(
x
2
−
1
)
U
n
−
1
(
x
)
2
=
1
{\displaystyle T_{n}(x)^{2}-(x^{2}-1)U_{n-1}(x)^{2}=1}
Вони задовольняють рівність:
T
n
(
x
)
+
U
n
−
1
(
x
)
x
2
−
1
=
(
x
+
x
2
−
1
)
n
.
{\displaystyle T_{n}(x)+U_{n-1}(x){\sqrt {x^{2}-1}}=(x+{\sqrt {x^{2}-1}})^{n}.}
З останньої рівності також випливають формули:
T
n
(
x
)
=
(
x
+
x
2
−
1
)
n
+
(
x
−
x
2
−
1
)
n
2
=
∑
k
=
0
⌊
n
/
2
⌋
(
n
2
k
)
(
x
2
−
1
)
k
x
n
−
2
k
;
{\displaystyle T_{n}(x)={\frac {(x+{\sqrt {x^{2}-1}})^{n}+(x-{\sqrt {x^{2}-1}})^{n}}{2}}=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n}{2k}}(x^{2}-1)^{k}x^{n-2k};}
U
n
(
x
)
=
(
x
+
x
2
−
1
)
n
+
1
−
(
x
−
x
2
−
1
)
n
+
1
2
x
2
−
1
=
∑
k
=
0
⌊
n
/
2
⌋
(
n
+
1
2
k
+
1
)
(
x
2
−
1
)
k
x
n
−
2
k
.
{\displaystyle U_{n}(x)={\frac {(x+{\sqrt {x^{2}-1}})^{n+1}-(x-{\sqrt {x^{2}-1}})^{n+1}}{2{\sqrt {x^{2}-1}}}}=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n+1}{2k+1}}(x^{2}-1)^{k}x^{n-2k}.}
Поліноми Чебишова першого роду
T
n
(
x
)
{\displaystyle T_{n}(x)}
T
n
(
cos
(
θ
)
)
=
cos
(
n
θ
)
.
{\displaystyle T_{n}(\cos(\theta ))=\cos(n\theta ).\,}
або,
T
n
(
x
)
=
cos
(
n
arccos
x
)
=
cosh
(
n
a
r
c
c
o
s
h
x
)
{\displaystyle T_{n}(x)=\cos(n\arccos x)=\cosh(n\,\mathrm {arccosh} \,x)\,\!}
Поліноми Чебишова другого роду
U
n
(
x
)
{\displaystyle U_{n}(x)}
U
n
(
cos
(
θ
)
)
=
sin
(
(
n
+
1
)
θ
)
sin
θ
.
{\displaystyle U_{n}(\cos(\theta ))={\frac {\sin((n+1)\theta )}{\sin \theta }}.}
Можна також виразити через гіперболічні функції
T
n
(
x
)
=
c
h
(
n
A
r
c
h
x
)
{\displaystyle T_{n}(x)=\mathrm {ch} (n\,\mathrm {Arch} \,x)}
та
U
n
(
x
)
=
s
h
(
n
A
r
c
h
x
)
.
{\displaystyle U_{n}(x)=\mathrm {sh} (n\,\mathrm {Arch} \,x).}
Із цих рівнянь випливають рівняння
T
n
(
x
)
=
1
/
2
[
(
x
+
i
1
−
x
2
)
n
+
(
x
−
i
1
−
x
2
)
n
]
,
{\displaystyle T_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}+(x-i{\sqrt {1-x^{2}}})^{n}],}
U
n
(
x
)
=
1
/
2
[
(
x
+
i
1
−
x
2
)
n
−
(
x
−
i
1
−
x
2
)
n
]
{\displaystyle U_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}-(x-i{\sqrt {1-x^{2}}})^{n}]}
якщо вважати
x
=
c
h
φ
{\displaystyle x=\mathrm {ch} \,\varphi }
гіперболічні функції у експониненційному вигляді, відзначивши, що
c
h
φ
+
s
h
φ
=
e
φ
{\displaystyle \mathrm {ch} \,\varphi +\mathrm {sh} \,\varphi =e^{\varphi }}
c
h
φ
−
s
h
φ
=
e
−
φ
.
{\displaystyle \mathrm {ch} \,\varphi -\mathrm {sh} \,\varphi =e^{-\varphi }.}
c
h
φ
{\displaystyle \mathrm {ch} \,\varphi }
x
,
{\displaystyle x,}
s
h
φ
{\displaystyle \mathrm {sh} \,\varphi }
(
x
2
−
1
)
1
/
2
.
{\displaystyle (x^{2}-1)^{1/2}.}
Поліноми Чебишова є розв'язками диференціальних рівнянь :
(
1
−
x
2
)
y
″
−
x
y
′
+
n
2
y
=
0
{\displaystyle (1-x^{2})\,y''-x\,y'+n^{2}\,y=0\,\!}
і
(
1
−
x
2
)
y
″
−
3
x
y
′
+
n
(
n
+
2
)
y
=
0
{\displaystyle (1-x^{2})\,y''-3x\,y'+n(n+2)\,y=0\,\!}
відповідно для поліномів першого і другого роду.
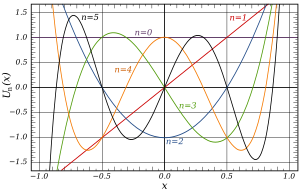
Поліноми Чебишева першого роду на відрізку−1 < x < 1 : T 0 T 1 T 2 T 3 T 4 T 5
T
0
(
x
)
=
1
{\displaystyle T_{0}(x)=1\,}
T
1
(
x
)
=
x
{\displaystyle T_{1}(x)=x\,}
T
2
(
x
)
=
2
x
2
−
1
{\displaystyle T_{2}(x)=2x^{2}-1\,}
T
3
(
x
)
=
4
x
3
−
3
x
{\displaystyle T_{3}(x)=4x^{3}-3x\,}
T
4
(
x
)
=
8
x
4
−
8
x
2
+
1
{\displaystyle T_{4}(x)=8x^{4}-8x^{2}+1\,}
T
5
(
x
)
=
16
x
5
−
20
x
3
+
5
x
{\displaystyle T_{5}(x)=16x^{5}-20x^{3}+5x\,}
T
6
(
x
)
=
32
x
6
−
48
x
4
+
18
x
2
−
1
{\displaystyle T_{6}(x)=32x^{6}-48x^{4}+18x^{2}-1\,}
T
7
(
x
)
=
64
x
7
−
112
x
5
+
56
x
3
−
7
x
{\displaystyle T_{7}(x)=64x^{7}-112x^{5}+56x^{3}-7x\,}
T
8
(
x
)
=
128
x
8
−
256
x
6
+
160
x
4
−
32
x
2
+
1
{\displaystyle T_{8}(x)=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1\,}
T
9
(
x
)
=
256
x
9
−
576
x
7
+
432
x
5
−
120
x
3
+
9
x
.
{\displaystyle T_{9}(x)=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x.\,}
Поліноми Чебишова другого роду на відрізку −1 < x < 1: U 0 U 1 U 2 U 3 U 4 U 5
U
0
(
x
)
=
1
{\displaystyle U_{0}(x)=1\,}
U
1
(
x
)
=
2
x
{\displaystyle U_{1}(x)=2x\,}
U
2
(
x
)
=
4
x
2
−
1
{\displaystyle U_{2}(x)=4x^{2}-1\,}
U
3
(
x
)
=
8
x
3
−
4
x
{\displaystyle U_{3}(x)=8x^{3}-4x\,}
U
4
(
x
)
=
16
x
4
−
12
x
2
+
1
{\displaystyle U_{4}(x)=16x^{4}-12x^{2}+1\,}
U
5
(
x
)
=
32
x
5
−
32
x
3
+
6
x
{\displaystyle U_{5}(x)=32x^{5}-32x^{3}+6x\,}
U
6
(
x
)
=
64
x
6
−
80
x
4
+
24
x
2
−
1
{\displaystyle U_{6}(x)=64x^{6}-80x^{4}+24x^{2}-1\,}
U
7
(
x
)
=
128
x
7
−
192
x
5
+
80
x
3
−
8
x
{\displaystyle U_{7}(x)=128x^{7}-192x^{5}+80x^{3}-8x\,}
U
8
(
x
)
=
256
x
8
−
448
x
6
+
240
x
4
−
40
x
2
+
1
{\displaystyle U_{8}(x)=256x^{8}-448x^{6}+240x^{4}-40x^{2}+1\,}
U
9
(
x
)
=
512
x
9
−
1024
x
7
+
672
x
5
−
160
x
3
+
10
x
.
{\displaystyle U_{9}(x)=512x^{9}-1024x^{7}+672x^{5}-160x^{3}+10x.\,}
Поліноми Чебишова мають такі властивості:
Ортогональність відносно скалярного добутку (з вагою
1
1
−
x
2
{\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}}
1
−
x
2
{\displaystyle {\sqrt {1-x^{2}}}}
∫
−
1
1
T
n
(
x
)
T
m
(
x
)
d
x
1
−
x
2
=
{
0
:
n
≠
m
π
:
n
=
m
=
0
π
/
2
:
n
=
m
≠
0
{\displaystyle \int _{-1}^{1}T_{n}(x)T_{m}(x)\,{\frac {dx}{\sqrt {1-x^{2}}}}={\begin{cases}0&:n\neq m\\\pi &:n=m=0\\\pi /2&:n=m\neq 0\end{cases}}}
∫
−
1
1
U
n
(
x
)
U
m
(
x
)
1
−
x
2
d
x
=
{
0
:
n
≠
m
,
π
/
2
:
n
=
m
.
{\displaystyle \int _{-1}^{1}U_{n}(x)U_{m}(x){\sqrt {1-x^{2}}}\,dx={\begin{cases}0&:n\neq m,\\\pi /2&:n=m.\end{cases}}}
Серед усіх поліномів, значення яких на відрізку
[
−
1
,
1
]
{\displaystyle [-1,1]}
найбільший старший коефіцієнт;
найбільше значення у довільній точці
a
≥
1
{\displaystyle a\geq 1}
Нулі полінома Чебишова є оптимальними вузлами інтерполяційних схем .
![{\displaystyle \ [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3175907f761b9e16bc6c405d2b521caa35e8062d)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
![{\displaystyle T_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}+(x-i{\sqrt {1-x^{2}}})^{n}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1f80e97a8a97d4c1653c87e660bc2919e4510ca)
![{\displaystyle U_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}-(x-i{\sqrt {1-x^{2}}})^{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/412ed460909a14484964cefc2b8723da32ae9fd1)
![{\displaystyle U_{n}(x)=1/2[(x+i{\sqrt {1-x^{2}}})^{n}-(x-i{\sqrt {1-x^{2}}})^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0747d3405d98e6bfcf54423329d46271f0dfc9b)
).svg)
).svg)
