Циркулянтний граф

Граф Пелі 13-о порядку як приклад циркулянтного графа.

Корона з шістьма, вісьмома, і десятьма вершинами.

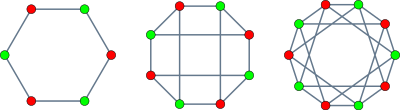
В теорії графів циркулянтним графом називається неорієнтований граф, який має циклічну групу симетрій, яка включає симетрію, при якій граф переводить вершину в будь-яку іншу вершину.

Еквівалентні визначення

Циркулянтні графи можуть бути визначені кількома еквівалентними способами:

• Автоморфізм групи графа містить циклічну підгрупу, яка діє транзитивно на вершини графа.
• Граф має матрицю суміжності, що є циркулянтною матрицею.
• $n$ вершин графа можна пронумерувати числами від 0 до n− 1 таким чином, що якщо дві вершини з номерами $x$ та $y$ суміжні, то будь-які дві вершини з номерами $z$ і (z−x+y) modn теж суміжні.
• Граф можна намалювати (з можливими перетинами ребер) так, що його вершини лежать в кутах правильного багатокутника та будь-який поворот багатокутника в себе є симетрією малюнка (отримуємо той же малюнок).

Приклади

Будь-який цикл є циркулянтним графом, як і будь-яка корона.

Графи Пелі порядку $n$ (де $n$ — просте число, порівнянне з 1 по модулю 4) — це графи, в яких вершини є числами від 0 до n− 1 і дві вершини суміжні, якщо різниця відповідних чисел є квадратичним відрахуванням по модулю $n$. Внаслідок того, що присутність або відсутність ребра залежить лише від різниці номерів вершин по модулю $n$, будь-який граф Пелі є циркулянтним графом.

Будь-які драбини Мебіуса є циркулянтним графом, як і будь-який повний граф. Повний двочастковий граф є циркулянтним, якщо обидві його частини мають однакову кількість вершин.

Якщо два числа $m$ та $n$ взаємно прості, то m×n туровий граф (граф, що має вершину в кожній клітині шахової дошки m×n та ребра між будь-якими двома клітинами, якщо тура може перейти з однієї клітини на іншу за один хід) є циркулянтним графом. Це є наслідком того, що його симетрії містять як підгрупу циклічну групу . Як узагальнення цього випадку, декартів добуток графів між будь-якими циркулянтними графами з $m$ та $n$ вершинами дає внаслідок циркулянтний граф.

Багато з відомих нижніх меж чисел Ремзі з'являються з прикладів циркулянтних графів, що мають маленькі максимальні кліки та маленькі максимальні незалежні множини.

Конкретний приклад

Циркулянтний граф $C_{n}^{s_{1},\ldots ,s_{k}}$ з межами $s_{1},\ldots ,s_{k}$ визначається як граф з $n$ вузлами, пронумерованими числами $0,1,\ldots ,n-1$ та кожний вузел $i$ суміжний з 2k вузлами $i\pm s_{1},\ldots ,i\pm s_{k}$ по модулю $n$.

• Граф $C_{n}^{s_{1},\ldots ,s_{k}}$ пов'язаний тоді і лише тоді, коли НСД$(n,s_{1},\ldots ,s_{k})=1$.

• Якщо $1\leq s_{1}<\cdots <s_{k}$ фіксовані цілі, то число остовних дерев $t(C_{n}^{s_{1},\ldots ,s_{k}})=na_{n}^{2}$, де $a_{n}$ задовольняє рекурентне співвідношення порядку $2^{s_{k}-1}$.
• Зокрема, $t(C_{n}^{1,2})=nF_{n}^{2}$, де $F_{n}$ — n-е число Фібоначчі.

Самодоповняльні циркулянти

Самодоповняльний граф — це граф, в якому видалення наявних ребер та додавання відсутніх дає граф, ізоморфний вихідному. Наприклад, циклічний граф з п'ятьма вершинами самодоповняльний і є також циркулянтним. У більш загальному вигляді, будь-який граф Пелі є самодоповняльним циркулянтним графом. Хорст Сакс показав, що якщо число $n$ має властивість, що будь-який простий дільник $n$ порівнюваний з 1 по модулю 4, то існує самодоповняльний циркулянтний граф з $n$ вершинами. Він висловив гіпотезу, що ця умова необхідна, тобто при інших значеннях $n$ самодоповняльні циркулянтні графи не існують. Гіпотезу через 40 років довів Вілфред (Vilfred).

Гіпотеза Адамса

Визначимо циркулянтну нумерацію циркулянтних графів як маркування вершин графа числами від 0 до n− 1 таким чином, що якщо дві вершини $x$ та $y$ суміжні, то будь-які дві вершини з номерами $z$ і (z−x+y) modn теж суміжні. Еквівалентно, циркулянтна нумерація — це нумерація вершин, при якій матриця суміжності графа є циркулянтною матрицею.

Нехай $a$ — ціле, взаємно просте з $n$, і нехай $b$ — будь-яке ціле число. Тоді лінійна функція ax+b перетворить циркулянтну нумерацію в іншу циркулянтну нумерацію. Андраш Адам (András Ádám) висловив гіпотезу, що лінійне відображення — єдиний спосіб перенумерації вершин графа, що зберігає властивість циркулянтності. Тобто, якщо $G$ та $H$ — два ізоморфних циркулянтних графи з різною нумерацією, то існує лінійне перетворення, що переводить нумерацію для $G$ в нумерацію для $H$. Однак, як з'ясувалося, гіпотеза Адама не вірна. Контрприкладом служать графи $G$ та $H$ з 16-тьма вершинами в кожному; вершина $x$ в $G$ з'єднана з шістьма сусідами x± 1, x± 2, і x± 7 (по модулю 16), в той час як в $H$ шість сусідів — це x± 2, x± 3, і x ± 5 (по модулю 16). Ці два графи ізоморфні, але їх ізоморфізм не можна отримати за допомогою лінійного перетворення.

Посилання

• Weisstein, Eric W. Circulant Graph(англ.) на сайті Wolfram MathWorld.