Граф без клешень

Матеріал з Вікіпедії — вільної енциклопедії.
Перейти до навігації Перейти до пошуку

У теорії графів графом без клешень називається граф, який не містить клешень, як породжених підграфів.

Клешня

Клешнею називається повний двочастковий граф K1,3 (тобто, зірка з трьома ребрами, трьома листками і однією центральною вершиною). Граф без клешень — це граф, в якому кожен породжений підграф не є клешнею. Тобто будь-яка підмножина з чотирьох вершин не є зіркою з трьома ребрами, що виходять з центральної вершини. Також можливо визначити граф без клешень, як граф, в якому окіл будь-якої вершини утворює доповнення графу без трикутників.

Графи без клешень спочатку вивчалися як узагальнення реберних графів і викликали додатковий інтерес лише тоді, коли було зроблено три ключових відкриття про графи без клешень:

  1. усі зв'язні графи без клешень парного порядку мають досконалі парування;
  2. відкриття поліноміального за часом алгоритму пошуку максимальних незалежних множин у графах без клешень;
  3. опис досконалих графів без клешень[1];

Графам без клешень присвячені сотні статей і кілька оглядів[2].

Приклади

[ред. | ред. код]
Правильний ікосаедр, багатогранник, вершини і ребра якого формують граф без клешень.
  • Реберний граф L(G) будь-якого графу G не має клешень. L(G) містить вершину для кожної дуги G , і вершини є суміжними в L(G) коли відповідні ребра мають спільну вершину в G. Реберний граф L(G) не може мати клешень, оскільки, якщо кожне з трьох ребер e1, e2, і e3 графу G має загальну вершину з четвертим ребром e4, то згідно з принципом Діріхле щонайменше 2 ребра з e1, e2, і e3 мають спільну вершину. Реберні графи можуть бути описані дев'ятьма забороненими підграфами[3], і клешня є найпростішим з цих дев'яти графів. Це дає мотив для вивчення графів без клешень[1].
  • Граф де Брейна[en] (графи, вершини яких відповідають n-бітовим двійковим рядкам для деякого n, а дуги відповідають (n−1)-бітним збігам двох рядків) не мають клешень. Один із способів показати це — побудувати граф де Бройна для n-бітових рядків як реберний граф від графу де Брейна для (n−1)-бітних рядків.
  • Доповнення будь-якого графу без трикутників не має клешень[4]. Ці графи включають будь-який повний граф як особливий випадок.
  • Належні інтервальні графи[en] (інтервальні графи, утворені як графи перетинів сімейств інтервалів, де жоден інтервал не містить інший інтервал сімейства) не мають клешень, оскільки чотири таких інтервали не можуть перетинатися за схемою клешні.[4]
  • Веретено Мозера (граф, що має сім вершин та використовується для доведення нижньої межі хроматичного числа площини) не має клешень.
  • Графи деяких багатогранників і політопів не мають клешень. Сюди входять граф тетраедра і взагалі будь-який симплекс (повний граф), граф октаедра і, в загальному випадку, будь-який крос-політоп (ізоморфний граф-ізоморфен, який утворюється завдяки видаленню досконалого парування з повного графу), граф правильного ікосаедра[5], і граф гексадекахорона.
  • Граф Шлефлі, сильно регулярний граф, що має 27 вершин, не має клешень[5].

Розпізнавання

[ред. | ред. код]

Можна перевірити безпосередньо, що заданий граф з n вершинами і m ребрами не має клешень за час O(n4)) шляхом перевірки кожної четвірки вершин — чи не породжують вони клешню[6]. Трохи ефективніше, але складніше, можна перевірити, чи не має граф клешень шляхом перевірки для кожної вершини графу, що доповнення графу сусідів вершини не містить трикутника. Граф містить трикутник в тому і тільки в тому випадку, якщо куб матриці інциндентності містить ненульовий діагональний елемент, так що пошук трикутника може бути здійснений за той же асимптотичний час, що і множення матриць n × n.[7] Таким чином, при використанні алгоритму Копперсміта—Винограда, загальний час визначення, чи є у графу клешні, становить O(n3.376).

Клокс, Крач і Мюллер[8] звернули увагу на те, що в графі без клешень кожна вершина має максимум сусідів, в іншому випадку згідно з теоремою Турана околиця вершини не матиме достатнє число ребер, щоб сформувати додаток графу без трикутників. Це спостереження дозволяє перевірити сусідів з використанням згаданого раніше алгоритму швидкого добутку матриць за той же асимптотичний час . Найгірший випадок цього алгоритму виникає, коли Ω(√m) вершин мають по Ω(√m) сусідів кожна, а решта вершин мають мало сусідів, у цьому випадку загальний час дорівнює (m3.376/2) = O(m1.688).

Перерахування

[ред. | ред. код]

Оскільки графи без клешень мають усі доповнення графів без трикутників, число графів без клешень з n вершинами росте як мінімум з тією ж швидкістю, що і число графів без трикутників, тобто, по експоненті від кореня з n. Число зв'язкових графів без клешень з n ребрами для n = 1, 2, … складає:

1, 1, 2, 5, 14, 50, 191, 881, 4494, 26389, 184749, … послідовність A022562 з Онлайн енциклопедії послідовностей цілих чисел, OEIS.

Якщо графи незв'язні, їх число збільшується:

1, 2, 4, 10, 26, 85, 302, 1285, 6170, … послідовність A086991 з Онлайн енциклопедії послідовностей цілих чисел, OEIS.

Техніка Палмера, Ріда і Робінсона[9] дозволяє порахувати число кубічних графів без клешень дуже ефективно, що є незвичним для задач на перерахування графів.

Парування

[ред. | ред. код]
Доведення Самнера, що зв'язні графи без клешень парного порядку мають досконале парування: видалення двох суміжних вершин v і w, найбільш віддалених від u, залишає підграф зв'язковим, що дозволяє продовжити процес.

Самнер[10] і, незалежно, Лас Вергнас[11] довели, що будь-який зв'язний граф без клешень з парним числом вершин має досконале парування[12]. Тобто існує безліч ребер в графі так, що кожна вершина є кінцевою вершиною в точності одного ребра з парування. З цього випливає, що для реберних графів, що мають парне число ребер, можна розбити всі ребра на шляхи довжиною два. Досконалі парування можуть бути використані для ще однієї характеристики графів без клешень — це точно ті графи, в яких будь-який зв'язний породжений підграф парного порядку має досконале парування[12].

Доведення Самнера показує, що в будь-якому зв'язковому графі без клешень можна знайти пару сполучених вершин, видалення яких залишає граф зв'язковим. Для доведення цього Самнер знаходить пару вершин u і v, які як можна більше віддалені один від одного, і вибирає w серед сусідів вершини v, віддалену від u наскільки можливо. Як він показав, ні v, ні w не можуть лежати на найкоротшому шляху від будь-якої іншої вершини до u, так що видалення вершин v і w залишає граф зв'язковим. Послідовне видалення таких пар утворює досконале парування в графі без клешень.

Та ж сама ідея доведення працює і в загальнішому випадку: якщо u — будь-яка вершина, v — будь-яка вершина, максимально віддалена від u, і w — будь-яка сусідня вершина для v, максимально віддалена від u. Тепер видалення v і w з графу не змінює відстаней до u. Таким чином, процес формування парування шляхом знаходження та видалення пар vw, максимально віддалених від u, може бути здійснений за лінійний час простим обходом дерева пошуку вшир, розпочатого з вершини u. Хробак, Наор і Новик[13] дали інший лінійний за часом алгоритм, заснований на пошуку вглиб, а також ефективні паралельні алгоритми для тієї ж задачі. Фаудрі, Фландрін и Ріяче[2] отримали кілька схожих результатів, зокрема:

  1. (r − 1)-зв'язний граф, що не містить K1,r підграфів непарного порядку, має досконалі парування для будь-якого r ≥ 2;
  2. графи непарного порядку без клешень з максимум однією вершиною степені один можуть бути поділені на один непарний цикл і парування;
  3. для будь-якого k, не меншого за половину мінімальної степені графу без клешень, у якому або k, або число вершин парно, граф має k-фактор;
  4. якщо граф без клешень є (2k + 1)-зв'язним, то будь-які k-реберні парування можуть бути розширені до досконалого парування.

Незалежні множини

[ред. | ред. код]
Немаксимальна незалежна множина (дві фіолетові вершини) і доповнюючий шлях.

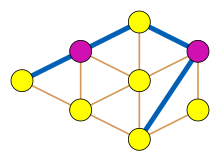
Незалежна множина в реберному графі відповідає паруванню у вихідному графі, тобто набору ребер, в якому ніякі два ребра не мають спільних точок. Як показав Едмондс[14], максимальне парування в будь-якому графі можна знайти за поліноміальний час; Сбіхі[15] розширив цей алгоритм так, що новий алгоритм знаходить максимальну незалежну множину в будь-якому графі без клешень[16]. Мінті[17], виправлений Накамурою і Тамурою,[18] дав інше розширення алгоритмів Едмонда для графів без клешень, перетворюючого задачу на пошук парування у допоміжному графі, отриманого із вихідного графу без клешень . Підхід Мінті може бути використаний для вирішення за поліноміальний час більш загальної задачі знаходження незалежної множини максимальної ваги. Існує узагальнення цих результатів на широкий клас графів.[16]

Як зауважив Сбіхі, якщо  — незалежна множина в графі без клешень, то будь-яка вершина графу може мати максимум дві сусідні вершини з  — три сусідні вершини утворили б вже саму клешню. Сбіхі називає вершину насиченою, якщо вона має дві сусідні вершини з , і ненасиченою, якщо вона не належить, і, в той же час, має менше двох сусідів з . Зі спостереження Сбіхі випливає, що, якщо і є незалежні множини, то граф, породжений , повинен мати ступінь не вище другого. Таким чином, він є об'єднанням шляхів і циклів. Зокрема, якщо  — не максимальна незалежна множина, вона відрізняється від будь-якої максимальної незалежної множини циклами і поповнюючими шляхами, тобто шляхами, в яких вершини з і не з чергуються, і у яких обидві кінцеві вершини не насичені. Симетрична різниця графів і поповнюючого шляха є максимальна незалежна множина (симетрична різниця графів H і G, що мають один і той же набір вершин V — це граф з тим же набором вершин V, що містить ребра G і H, але не містить загальних ребер, що належать як G, так і H). Алгоритм Сбіхі послідовно збільшує розмір незалежної множини шляхом знаходження поповнюючих шляхів, доки такі можна знайти.

Знаходження поповнюючого шляху є складним завданням, оскільки поширення шляху може і не існувати, якщо він містить ребро між двома вершинами, що не належать . На щастя, це може статися тільки в двох випадках: дві суміжні вершини можуть бути кінцевими вершинами шляху, або між ними лежить одна вершина, суміжна обом. Будь-яка інша суміжна вершина призведе до клешні. Суміжних кінцевих вершин можна позбутися, тимчасово видаляючи всі суміжні v вершини перед пошуком поповнюючого шляху, початківця в v. Якщо знайдений шлях не буде входити у вершину v, можна видалити його з графу до кінця алгоритму. Після такої редукції графу завдання може бути описано в термінах графу-перемикача[en], хоча Сбіхі і не користувався цією термінологією. Граф-перемикач — це ненаправлений граф, в якому дуги будь-якої вершини розділені на дві групи, і будь-який шлях, що проходить через вершину, зобов'язаний містити ребра з обох груп. Можна побудувати граф-перемикач на множині насичених і ненасичених вершин графу без клешень, ребра якого з'єднують вершини, якщо вони не є суміжними у вихідному графі, і існує шлях довжини 2 між ними, що проходить через вершину з I. Дві множини ребер в кожній вершині утворюються двома вершинами I, через які ці шляхи, довжиною 2, проходять. Шлях у графі-перемикачі між двома ненасиченими вершинами відповідає поповнюючому шляху у вихідному графі. Граф-перемикач має квадратичну складність, і шлях у ньому може бути знайдений за лінійний час, а за весь час роботи алгоритму можуть знадобитися O(n) поповнюючих шляхів, які необхідно знайти. Таким чином, алгоритм Сбіхі вимагає O(n3) часу роботи.

Розфарбовування, кліки, і домінування

[ред. | ред. код]

Досконалий граф — це граф, в якому хроматичне число дорівнює розміру максимальної кліки, і в якому ця рівність зберігається у всіх породжених підграфах. Відомо (зі сильної теореми про досконалі графи), що досконалі графи можуть бути охарактеризовані як графи, що не мають непарних циклів чи доповнень непарним циклам (так звані непарні діри) як індукованих підграфів[5]. Проте багато років цей факт залишався гіпотезою, доведеною тільки для спеціальних підкласів графів. Одним з таких підкласів було сімейство графів без клешень — кілька авторів виявили, що графи без клешень і без непарних циклів і дірок досконалі. Досконалість графу без клешень може бути перевірена за поліноміальний час. У досконалому графі без клешень околиця будь-якої вершини утворює доповнення двочасткового графу. Можна розфарбувати досконалий граф без клешень або знайти в ньому максимальну кліку за поліноміальний час[19].

Якщо граф без клешень не досконалий, завдання пошуку максимальної кліки стає NP-задачею[6]. Задача знаходження оптимального розфарбування такого графу також є NP-задачею, оскільки (через реберний граф) ця задача узагальнює NP-завдання обчислення хроматичного числа графу[6]. З тієї ж причини NP-завданням є пошук алгоритму розфарбовування, гарантована ефективність якого краще, ніж 4/3. Однак гарантовану ефективність, рівну двом, можна отримати в алгоритмі жадібного розфарбовування, оскільки хроматичне число графу без клешень більше, ніж половина його максимального ступеня.

Хоча не всі графи без клешень досконалі, графи без клешень задовільняють іншій властивості, пов'язаній з досконалістю. Граф називається досконалим графом домінування, якщо він має мінімальну домінуючу множину, що є незалежною множиною вершин, і якщо тією ж властивістю володіють всі породжені підграфи. Графи без клешень володіють цією властивістю. Щоб показати це, уявимо, що D — домінуюча множина в графі без клешень, і нехай v і w — дві сполучені вершини D. Тоді безліч вершин, домінованих вершиною v, але не w, повинно бути кліком (в іншому випадку v виявиться центром клешні). Якщо кожна вершина цієї кліка вже домінується принаймні одним членом множини D, то v може бути видалена з породженням меншої незалежної домінуючої множини. В іншому ж випадку v можна замінити однією з недомінуючих вершин з кліка, породжуючи домінуючу множину з меншим числом суміжних вершин. Повторюючи ці заміни, ми досягнемо домінуючої множини, що не перевершує D, так що, якщо початкове D — мінімальна домінуюча множина, процес закінчиться створенням рівної за розміром незалежної домінуючої множини[20].

Незважаючи на властивість досконалого домінування, визначення розміру мінімальної домінуючої множини в графі без клешень є NP-завданням[6]. Однак в контраст з більш загальними класами графів, пошук мінімальної домінуючої множини в графі без клешень володіє параметичною складністю з фіксованими параметрами[en] — завдання може бути вирішено за час, поліноміально залежний від розміру графу і експоненціально від розміру домінуючої множини[21][22].


Структура

[ред. | ред. код]

У серії статей Чудновська і Сеймур[23] довели структурну теорію графів без клешень, аналогічну для сімейств мінорно-замкнутих графів, доведену Робертсоном і Сеймуром, і структурній теорії для досконалих графів, яку Чудновська, Сеймур та їх співавтори використовували для доведення теореми про строго досконалий граф[5]. Теорія занадто складна, але можливо описати декілька її наслідків. По-перше, для спеціального підкласу графів без клешень, який вони назвали квазіреберні графи (або локально квазідвудольні графи), вони стверджують, що кожен такий граф має одну з двох форм:

  1. Нечіткий коловий інтервальний граф — клас графів, які геометрично можна представити як точки і дуги на колі.
  2. Граф, який можна побудувати з мультиграфу шляхом заміни кожного ребра нечітким лінійним інтервальним графом. Це узагальнює конструкцію реберних графів, в яких кожне ребро мультиграфу замінюється вершиною. Нечіткі лінійні інтервальні графи будуються так само, як і нечіткі колові інтервальні графи, тільки на відрізку, а не на колі.

Чудновська і Сеймур класифікували довільні зв'язні графи без клешень наступним чином:

  1. Шість специфічних графів без клешень. Три з них є реберними графами, деякі — графи дуг кола і останні — породжені підграфи ікосаедра. Решта три вимагають додаткових визначень.
  2. Графи, утворені чотирма простими способами з менших графів без клешень.
  3. Антипризматичні графи — клас щільних графів, визначаються як графи без клешень, в яких будь-які чотири вершини породжують підграф з мінімум двома ребрами.

Більша частина їх роботи з класифікації присвячена аналізу антипризматичних графів. Граф Шлефлі, сильно регулярний граф без клешень з параметрами srg (27,16,10,8), відіграє важливу роль у цій частині аналізу. Ця структурна теорія призвела до нового просування в комбінаториці багатогранників і нових кордонів хроматичних чисел графів без клешень[5], а також до нових алгоритмів параметричної складності з фіксованими параметрами для домінуючих множин в графах без клешень[22].

Посилання

[ред. | ред. код]
  • Claw-free graphs, інформаційна система на Graph Class Inclusions
  • Mugan, Jonathan William; Weisstein, Eric W. Claw-Free Graph(англ.) на сайті Wolfram MathWorld.

Джерела

[ред. | ред. код]
  1. ↑ а б Faudree, Flandrin, Ryjáček, 1997, с. 88.
  2. ↑ а б Faudree, Flandrin, Ryjáček, 1997.
  3. ↑ L. W. Beineke. Beiträge zur Graphentheorie. — Teubner, 1968. — С. 17—33.
  4. ↑ а б Faudree, Flandrin, Ryjáček, 1997, с. 89.
  5. ↑ а б в г д Maria Chudnovsky, Neil Robertson, Paul Seymour, Robin Thomas. Архівована копія // Annals of Mathematics. — 2006. — Т. 164, вип. 1. — DOI:10.4007/annals.2006.164.51. Архівовано з джерела 11 жовтня 2015. Процитовано 30 жовтня 2015. (англ.)
  6. ↑ а б в г Faudree, Flandrin, Ryjáček, 1997, с. 132.
  7. ↑ Alon Itai, Michael Rodeh. Finding a minimum circuit in a graph // SIAM Journal on Computing. — 1978. — Т. 7, вип. 4. — С. 413—423. — DOI:10.1137/0207033.
  8. ↑ Ton Kloks, Dieter Kratsch, Haiko Müller.  // Information Processing Letters. — 2000. — Т. 74, вип. 3—4. — С. 115—121. — DOI:10.1016/S0020-0190(00)00047-8.
  9. ↑ Edgar M. Palmer, Ronald C. Read, Robert W. Robinson. Counting claw-free cubic graphs // SIAM Journal on Discrete Mathematics. — 2002. — Т. 16, вип. 1. — С. 65—73. — DOI:10.1137/S0895480194274777.
  10. ↑ David P. Sumner. Graphs with 1-factors // Proceedings of the American Mathematical Society. — American Mathematical Society, 1974. — Т. 42, вип. 1. — С. 8—12. — DOI:10.2307/2039666.
  11. ↑ M. Las Vergnas. A note on matchings in graphs // Cahiers du Centre d'Études de Recherche Opérationnelle. — 1975. — Т. 17, вип. 2—3—4. — С. 257—260.
  12. ↑ а б Faudree, Flandrin, Ryjáček, 1997, с. 120—124.
  13. ↑ Marek Chrobak, Joseph Naor, Mark B. Novick. Algorithms and Data Structures: Workshop WADS '89, Ottawa, Canada, August 1989, Proceedings[en]. — Springer, 1989. — Т. 382. — С. 147—162. — DOI:10.1007/3-540-51542-9_13.
  14. ↑ Jack Edmonds. Paths, Trees and Flowers // Canadian J. Math. — 1965. — Т. 17, вип. 0. — С. 449—467. — DOI:10.4153/CJM-1965-045-4.
  15. ↑ Najiba Sbihi. Algorithme de recherche d'un stable de cardinalité maximum dans un graphe sans étoile // Discrete Mathematics. — 1980. — Т. 29, вип. 1. — С. 53—76. — DOI:10.1016/0012-365X(90)90287-R. (фр.)
  16. ↑ а б Faudree, Flandrin, Ryjáček, 1997, с. 133—134.
  17. ↑ George J. Minty. On maximal independent sets of vertices in claw-free graphs // Journal of Combinatorial Theory. Series B. — 1980. — Т. 28, вип. 3. — С. 284—304. — DOI:10.1016/0095-8956(80)90074-X. (англ.)
  18. ↑ Daishin Nakamura, Akihisa Tamura. A revision of Minty's algorithm for finding a maximum weighted stable set of a claw-free graph // Journal of the Operations Research Society of Japan. — 2001. — Т. 44, вип. 2. — С. 194—204. Архівовано з джерела 3 березня 2016. Процитовано 30 жовтня 2015. (англ.)
  19. ↑ Faudree, Flandrin, Ryjáček, 1997, с. 135—136.
  20. ↑ Faudree, Flandrin, Ryjáček, 1997, с. 124—125.
  21. ↑ Marek Cygan, Geevarghese Philip, Marcin Pilipczuk, Michał Pilipczuk, Jakub Onufry Wojtaszczyk. Dominating set is fixed parameter tractable in claw-free graphs. — 2010.
  22. ↑ а б Danny Hermelin, Matthias Mnich, Erik Jan van Leeuwen, Gerhard Woeginger. Domination when the stars are out. — 2010.
  23. ↑ Maria Chudnovsky, Paul Seymour. Surveys in combinatorics 2005 год. — Cambridge Univ. Press, 2005. — Т. 327. — С. 153—171.

Література

[ред. | ред. код]
  • Ralph Faudree, Evelyne Flandrin, Zdeněk Ryjáček.  // Discrete Mathematics. — 1997. — Т. 164, вип. 1—3. — С. 87—147. — DOI:10.1016/S0012-365X(96)00045-3.
Отримано з https://uk.wikipedia.org/wiki/Граф_без_клешень