Фізичний маятник

Фізичний маятник.
$O$ — вісь підвісу;
$N$ — реакція осі підвісу;
$G$ — центр ваги;
$O'$ — центр гойдання;
$\lambda$ — зведена довжина;
$\theta$ — кут відхилення маятника від рівноваги;
$\alpha$ — початковий кут відхилення маятника;
$m$ — маса маятника;
$h$ — відстань від точки підвісу до центру ваги маятника;
$g$ — прискорення вільного падіння.

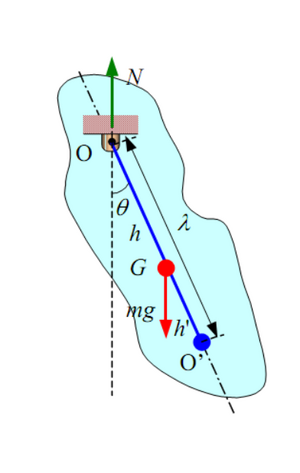
Фізи́чний ма́ятник — тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить через центр маси тіла.

Основні характеристики

Період коливань фізичного маятника визначається формулою:

$T={\frac {2\pi }{\omega }}=2\pi {\sqrt {\frac {I}{mgd}}}$,

де I — момент інерції, m — маса, d — віддаль від центра маси тіла до осі, g — прискорення вільного падіння.

Зведена довжина фізичного маятника — довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника. Вона дорівнює

$l_{r}={\frac {I}{md}}$.

Диференціальне рівняння руху фізичного маятника

Момент інерції відносно осі, що проходить через точку підвісу за теоремою Штейнера:

$I=I_{0}+mh^{2}=m\left(r^{2}+h^{2}\right),$

де $I_{0}$ — момент інерції відносно осі проходить через центр ваги;

$r$ — ефективний радіус інерції відносно осі, що проходить через центр ваги.

Динамічне рівняння довільного обертання твердого тіла:

$I{\frac {d^{2}\theta }{dt^{2}}}=-M_{s},$

де $M_{s}$ — сумарний момент сил, що діють на тіло відносно осі обертання.

$M_{s}=M+M_{f},$

де $M$ — момент сил, викликаний силою тяжіння;

$M_{f}$ — момент сил, викликаний силами тертя середовища.

Момент викликаний силою тяжіння залежить від кута відхилення тіла від положення рівноваги:

$M=mgh\sin \theta$

Якщо знехтувати опором середовища, диференціальне рівняння коливань фізичного маятника в полі сили тяжіння:

$I{\frac {d^{2}\theta }{dt^{2}}}=-mgh\sin \theta$.

Якщо розділити обидві частини рівняння на $h$ і покласти $\lambda ={\frac {r^{2}+h^{2}}{h}}={\frac {r^{2}}{h}}+h,$ то рівняння буде:

$\lambda {\frac {d^{2}\theta }{dt^{2}}}=-g\sin \theta .$

Таке рівняння аналогічне рівнянню коливань математичного маятника довжини $\lambda$. Величину $\lambda$ називають зведеною довжиною фізичного маятника.

Центр гойдання фізичного маятника

Центр гойдання — точка, в якій треба зосередити всю масу фізичного маятника, щоб його період коливань не змінився.

Помістимо на промені, що проходить від точки підвісу через центр ваги, точку на відстані $\lambda$ від точки підвісу. Ця точка і буде центром гойдання маятника.

Дійсно, якщо всю масу зосередити в центрі гойдання, то центр гойдання буде збігатися з центром ваги. Тоді момент інерції відносно осі підвісу дорівнюватиме $I=m\lambda ^{2}$, а момент сили тяжіння відносно тієї ж осі $-mg\lambda \sin \theta$. При цьому рівняння руху не зміниться.

Теорема Гюйгенса

Формулювання

Якщо фізичний маятник підвісити за центр гойдання, то його період коливань не зміниться, а колишня точка підвісу зробиться новим центром гойдання.

Доведення

Обчислимо зведену довжину нового маятника:

$\lambda _{1}={\frac {r^{2}}{r^{2}/h}}+{\frac {r^{2}}{h}}=h+{\frac {r^{2}}{h}}=\lambda$.

Збіг зведених довжин для двох випадків і доводить твердження теореми.

Період коливань фізичного маятника

Для того, щоб знайти період коливань фізичного маятника, необхідно розв'язати рівняння гойдання.

Для цього помножимо ліву $\lambda {\frac {d^{2}\theta }{dt^{2}}}=\lambda {\frac {d}{dt}}\left({\frac {d\theta }{dt}}\right)$ і праву частини цього рівняння на $d\theta$. Тоді:

$\lambda {\frac {d\theta }{dt}}d\left({\frac {d\theta }{dt}}\right)=-g\sin \theta \,d\theta$.

Інтегруючи це рівняння, отримуємо:

$\lambda \left({\frac {d\theta }{dt}}\right)^{2}=2g\cos \theta +C$,

де $C$ — довільна стала.

Її можна знайти з граничної умови, що в моменти $\theta =\pm \alpha \,\,\,,{\frac {d\theta }{dt}}=0$. Маємо:

$C=-2g\cos \alpha .$

Підставляємо і перетворюємо отримане рівняння:

${\frac {d\theta }{dt}}=2{\sqrt {\frac {g}{\lambda }}}{\sqrt {\sin ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\theta }{2}}}}.$

Відокремлюємо змінні й інтегруємо це рівняння:

${\sqrt {\frac {g}{\lambda }}}t=\int \limits _{0}^{\frac {\theta }{2}}{\frac {d\left({\frac {\theta }{2}}\right)}{\sqrt {\sin ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\theta }{2}}}}}.$

Зручно зробити заміну змінної $\sin {\frac {\theta }{2}}=\sin {\frac {\alpha }{2}}\sin \varphi$. Тоді шукане рівняння набуде вигляду:

$t={\sqrt {\frac {\lambda }{g}}}\int \limits _{0}^{\varphi }{\frac {d\varphi }{\sqrt {1-\sin ^{2}{\frac {\alpha }{2}}\sin ^{2}\varphi }}}={\sqrt {\frac {\lambda }{g}}}F\left(\varphi \setminus \alpha /2\right).$

Тут $F\left(\varphi \setminus \alpha \right)$ — нормальний еліптичний інтеграл Лежандра 1-го роду. Для періоду коливань отримуємо формулу:

$T=4{\sqrt {\frac {\lambda }{g}}}\,\int \limits _{0}^{\pi /2}{\frac {d\varphi }{\sqrt {1-\sin ^{2}{\frac {\alpha }{2}}\sin ^{2}\varphi }}}=4{\sqrt {\frac {\lambda }{g}}}\,K\left(\sin {\frac {\alpha }{2}}\right).$

Тут $K\left(\sin {\frac {\alpha }{2}}\right)$ — повний нормальний еліптичний інтеграл Лежандра 1-го роду. Розкладаючи його в ряд, можна отримати зручну для практичних обчислень формулу:

$T=2\pi {\sqrt {\frac {\lambda }{g}}}\left\{1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}\left({\frac {\alpha }{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}\left({\frac {\alpha }{2}}\right)+\dots +\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}\sin ^{2n}\left({\frac {\alpha }{2}}\right)+\dots \right\}.$

Період малих коливань фізичного маятника

Якщо $\alpha \ll 1,$ — випадок малих максимальних кутових відхилень від рівноваги, $\theta <\alpha ,$ то $\sin \theta \approx \theta$ оскільки розклад синуса в ряд Маклорена $\sin \theta \approx \theta -\theta ^{3}/3\dots$ і рівняння руху переходить у рівняння гармонійного осцилятора без тертя:

$\lambda {\frac {d^{2}\theta }{dt^{2}}}=-g\theta .$

Період коливань маятника в цьому випадку:

$T=2\pi {\sqrt {\frac {\lambda }{g}}}.$

В іншому формулюванні: якщо амплітуда коливань $\alpha$ мала, то корінь у знаменнику еліптичного інтеграла наближено дорівнює одиниці. Такий інтеграл легко береться, і виходить добре відома формула малих коливань:

$T=2\pi {\sqrt {\frac {\lambda }{g}}}=2\pi {\sqrt {\frac {I}{mgh}}}.$

Ця формула дає результати прийнятної точності (помилка менш 1 %) при кутах, що не перевищують 4°.

Наступний порядок наближення можна використовувати з прийнятною точністю (помилка менше 1 %) при кутах відхилення до 1 радіана (≈57°):

$T\approx 2\pi {\sqrt {\frac {\lambda }{g}}}\left(1+{\frac {1}{4}}\sin ^{2}\left({\frac {\alpha }{2}}\right)\right)={\frac {\pi }{4}}{\sqrt {\frac {\lambda }{g}}}\left(9-\cos {\alpha }\right).$

Див. також

• Маятник
• Математичний маятник
• Крутильний маятник
• Пружинний маятник

Посилання

• Маятник // Большая советская энциклопедия : в 30 т. / главн. ред. А. М. Прохоров. — 3-е изд. — М. : «Советская энциклопедия», 1969—1978. (рос.)
• Физический маятник // Большая советская энциклопедия : в 30 т. / главн. ред. А. М. Прохоров. — 3-е изд. — М. : «Советская энциклопедия», 1969—1978. (рос.)