Кирпатий двадцятичотирьохкомірник

Кирпатий двадцятичотирьохкомірник
Тип	однорідний 4-політоп
Символ Шлефлі	s{3,4,3} sr{3,3,4} s{31,1,1}
Діаграми Коксетера — Динкіна	або або
Комірок	144	96 3.3.3 (неправильний)  24 3.3.3 24 3.3.3.3.3
Граней	480 {3}
Ребер	432
Вершин	96
Вершинна фігура	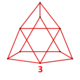(Тричі відсічений ікосаедр)
Групи симетрії	[3+,4,3], 12F4, порядок 576 [(3,3)+,4], 12B4, порядок 192 [31,1,1]+, 12D4, порядок 96
Двоїстий	Двоїстий кирпатий 24-комірник
Властивості	опуклий
Показник однорідності [уточнити]	30 31 32

Кирпа́тий двадцятичотирьохкомі́рник — чотиривимірний многогранник, один із 47 непризматичних опуклих однорідних багатокомірників і один із 3 напівправильних багатокомірників (бо складається з платонових тіл двох різних видів).

Вперше описав у статті 1900 року Торольд Госсет, який назвав багатокомірник тетрікосаедриком (tetricosahedric), оскільки його комірки - тетраедри та ікосаедри. Також відомий як кирпатий ікосітетрахор, напівкирпатий поліоктаедр (англ. semi-snub polyoctahedron).

Опис

Розгортка

Обмежений 144 тривимірними комірками - 120 правильними тетраедрами і 24 правильними ікосаедрами. Кожну ікосаедричну комірку оточують вісім ікосаедричних та дванадцять тетраедричних. Тетраедричні комірки поділяються на дві групи: 24 з них оточені чотирма тетраедричними, решта 96 — трьома ікосаедричними та тетраедричною.

480 двовимірних граней - однакові правильні трикутники. 96 граней розділяють дві ікосаедричні комірки, 96 граней — дві тетраедричні, інші 288 — ікосаедричну й тетраедричну.

Має 432 ребра рівної довжини. На 288 ребрах сходяться по три грані й по три комірки (дві ікосаедричні й тетраедрична), на решті 144 - по чотири грані й по чотири комірки (ікосаедрична та три тетраедричні).

Має 96 вершин. У кожній вершині сходяться по 9 ребер, по 15 граней і по 8 комірок (три ікосаедричні та п'ять тетраедричних).

Кирпатий двадцятичотирьохкомірник можна отримати з шестисоткомірника, відсікши від того 24 ікосаедричні піраміди — так, щоб замість них залишилися тільки їхні основи. Вершини отриманого багатокомірника - 96 зі 120 вершин шестисоткомірника (а видалені 24 вершини утворюють вершини звичайного двадцятичотирьохкомірника); ребра - 432 зі 720 ребер шестисоткомірника; грані - 480 із 1200 граней шестисоткомірника. Звідси ясно, що в кирпатого двадцятичотирьохкомірника теж існують описана і обидві напіввписані тривимірні гіперсфери, причому вони збігаються з описаною і напіввписаними гіперсферами початкового шестисоткомірника.

У координатах

Кирпатий двадцятичотирьохкомірник із довжиною ребра $2$ можна розмістити в декартовій системі координат так, щоб координати його вершин були різними парними перестановками наборів чисел $\left(0;\;\pm 1;\;\pm \Phi ;\;\pm \Phi ^{2}\right),$ де $\Phi ={\frac {1+{\sqrt {5}}}{2}}$ - відношення золотого перетину.

Початок координат $\left(0;\;0;\;0;\;0\right)$ буде при цьому центром симетрії багатокомірника, а також центром його описаної та напіввписаних гіперсфер.

Ортогональні проєкції на площину

Метричні характеристики

Якщо кирпатий двадцятичотирьохкомірник має ребро довжини $a,$ то його чотиривимірний гіпероб'єм і тривимірна гіперплоща поверхні виражаються відповідно як

$V_{4}=5\left({\frac {9}{4}}+{\sqrt {5}}\right)a^{4}\approx 22{,}4303399a^{4},$

$S_{3}=10\left(3+{\sqrt {2}}+{\sqrt {5}}\right)a^{3}\approx 66{,}5028154a^{3}.$

Радіус описаної гіперсфери (що проходить через усі вершини багатокомірника) при цьому дорівнює

$R=\Phi a={\frac {1}{2}}\left(1+{\sqrt {5}}\right)a\approx 1{,}6180340a,$

радіус зовнішньої напіввписаної гіперсфери (що дотикається до всіх ребер у їхніх серединах) -

$\rho _{1}={\frac {1}{2}}{\sqrt {5+2{\sqrt {5}}}}\;a\approx 1{,}5388418a,$

радіус внутрішньої напіввписаної гіперсфери (що дотикається до всіх граней у їхніх центрах)

$\rho _{2}={\frac {1}{6}}\left({\sqrt {15}}+3{\sqrt {3}}\right)a\approx 1{,}5115226a.$

Вписати в кирпатий двадцятичотирьохкомірник гіперсферу — так, щоб вона дотикалася до всіх комірок, — неможливо. Радіус найбільшої гіперсфери, яку можна помістити всередині кирпатого двадцятичотирьохкомірника з ребром $a$ (вона дотикатиметься лише до всіх ікосаедричних комірок у їхніх центрах), дорівнює

$r_{I}={\frac {1}{4}}\left(3+{\sqrt {5}}\right)a\approx 1{,}3090170a.$

Відстань від центру багатокомірника до будь-якої тетраедричної комірки перевищує $r_{I}$ і становить

$r_{T}={\frac {1}{4}}\left({\sqrt {10}}+2{\sqrt {2}}\right)a\approx 1{,}4976762a.$

Заповнення простору

За допомогою кирпатих двадцятичотирьохкомірників, шістнадцятикомірників і п'ятикоміриків можна без проміжків і накладень замостити чотиривимірний простір (див. Стільник з кирпатих 24-комірників). Це заповнення також знайшов Торольд Госсет.

Посилання

• Джордж Ольшевський. Print #11: Snub icositetrachoron net (англ.)