Границя

Границя — одне з основних понять функціонального аналізу (а також математичного аналізу, який є скінченновимірним випадком функціонального), яке означає, що деякий об'єкт, змінюючись, нескінченно наближається до певного сталого значення. Точний зміст отримує лише при наявності коректного визначення поняття близькості між елементами (точками) множини, в якій вказана величина набуває значення. Основні поняття математичного аналізу — неперервність, похідна, інтеграл — визначають через границю.

Границя послідовності

Стале число $a$ називають границею послідовності (варіанти) $x=x_{n}$, якщо для кожного додатного числа $\varepsilon$, скільки б малим воно не було, існує такий номер $N$, що всі значення $x_{n}$, в яких номер $n>N$, задовольняють нерівність

$|x_{n}-a|<\varepsilon$

Той факт, що $a$ є границею варіанти, позначають так: $\lim _{n\rightarrow \infty }x_{n}=a$ або просто $\lim x=a$ чи $x_{n}\rightarrow a,n\rightarrow \infty$. Номер $N$ залежить від вибору числа $\epsilon$. При зменшенні $\varepsilon$ число $N$ буде збільшуватись. Тобто, чим більш близьких значень $x_{n}$ до $a$ вимагати, тим ймовірніше більш далеких значення ряду доведеться розглядати.

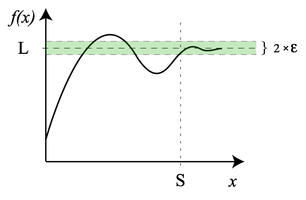
Границя функції

Точка x знаходиться в межах δ одиниць c, f(x) — в межах ε одиниць L.		Для всіх x > S, f(x) перебуває в межах ε із L.

Означення за Коші

Нехай $A\subset \mathbf {R} ,\quad f:A\to \mathbf {R}$, $x_{0}$ — гранична точка множини A. Число a називають границею функції $f$ у точці $x_{0}$, якщо

$\forall \varepsilon >0\quad \exists \delta =\delta (\varepsilon )>0\quad \forall x\in A\cap B(x_{0},\delta )\setminus \{x_{0}\}:|f(x)-a|<\varepsilon$

Позначення:

$a=\lim _{x\to x_{0}}{f(x)}$

або

$f(x)\to a$ при $x\to x_{0}$

Означення за Гейне

Число $A$ називають границею функції $f(x)$ в точці $x_{0}$, якщо для довільної послідовності $\left\{x_{n}\right\}_{n=1}^{\infty }$, що збігається до числа $x_{0}$, відповідна послідовність значеннь функції $\left\{f\left(x_{n}\right)\right\}_{n=1}^{\infty }$ збіжна і має границею одне і теж саме число $A$.

Див. також

• Границя функції в точці
• Верхня і нижня границі
• Границя інтегральних сум
• Границя послідовності множин
• Границя індуктивна
• Границя проективна
• Межа (значення)