Конгруентність (геометрія)

В геометрії, дві фігури конгруентні, якщо вони мають однакову форму та розмір. Більш формально, два набори точок називаються конгруентними тоді і тільки тоді, якщо один набір можна сумістити з іншим за допомогою ізометрії, тобто комбінації паралельного перенесення, обертання і відбиття.
В елементарній геометрії слово конгруентність часто використовують наведеним чином.[1] Слово рівність часто використовують замість конгруентності для простих об'єктів.
- Два відрізки будуть конгруентними, якщо вони мають однакову довжину.
- Два кути будуть конгруентними, якщо вони мають однакову величину.
- Два кола будуть конгруентними якщо вони мають однаковий діаметр.
В даному випадку сенс, що дві пласкі фігури є конгруентними передбачає, що їх відповідні характеристики є «конгруентними» або «рівними», включаючи не лише їх відповідні кути і сторони, але ще і відповідні діагоналі, периметри і площі.
Споріднене поняття подібності передбачає, що об'єкти мають однакову форму, але не обов'язково матимуть однаковий розмір.
Визначення конгруентності в аналітичній геометрії[ред. | ред. код]
В евклідовій системі, конгруентність — наріжне поняття; це відповідник рівності для чисел. В аналітичній геометрії, конгруентність може бути визначена інтуїтивно у такий спосіб: два відображення фігури на декартовій системі координат конгруентні тоді і тільки тоді, коли для будь-яких двох точок в першому відображенні евклідова відстань між ними дорівнює евклідовій відстані між двома відповідними точками в другому відображенні.
Більш формальне визначення: дві підмножини A та B евклідового простору Rn називаються конгруентними, якщо існує ізометрія f : Rn → Rn (елемент евклідової групи E(n)) з f(A) = B. Конгруентність є відношенням еквівалентності.
Конгруентність трикутників[ред. | ред. код]
Два трикутники конгруентні, якщо їхні відповідні сторони і кути рівні між собою.
Якщо трикутник ABC конгруентний трикутнику DEF, математично це може бути записано так:
В багатьох випадках цього достатньо, щоб встановити рівність трьох відповідних частин і використати один з наступних результатів для виведення конгруентності двох трикутників.
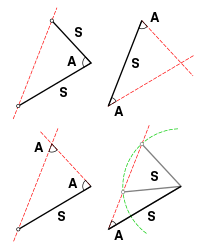
Визначення конгруентності[ред. | ред. код]
Достатньою ознакою конгруентності між двома трикутниками в евклідовому просторі може бути одна з наступних рівностей:
- ССС (Сторона-Сторона-Сторона): Якщо три пари сторін двох трикутників рівні за довжинами, тоді трикутники конгруентні.
- СКС (Сторона-Кут-Сторона): Якщо дві пари сторін двох трикутників рівні і кути між ними теж рівні, тоді трикутники конгруентні.
- КСК (Кут-Сторона-Кут): Якщо пара кутів двох трикутників рівна і сторони, що лежать між цими кутами у двох трикутниках, також рівні, тоді трикутники конгруентні
Постулат КСК був введений Фалесом Мілетським. В більшості систем аксіом, три критерії — СКС, ССС і КСК —впроваджені як теореми. - ККС (Кут-Кут-Сторона): Якщо дві пари кутів і відповідні сторони, що не лежать між ними в двох трикутниках, рівні, то трикутники конгруентні.
- ПГК (Прямий-кут-Гіпотенуза-Катет): Якщо два прямокутних трикутники мають рівні гіпотенузи і пару рівних катетів, вони конгруентні.
Сторона-Сторона-Кут[ред. | ред. код]
Умова ССК, яка визначається через дві сторони і кут, відмінний від утвореного ними (також відома як КСС або Кут-Сторона-Сторона), не доводить конгруентність. Для доведення конгруентності потрібна додаткова інформація, наприклад, величина відповідних кутів і, в деяких випадках, довжини двох пар відповідних сторін. Тут можливі чотири випадки: Якщо два трикутники задовольняють умові ССК і відповідні кути є тупими або прямими, тоді трикутники конгруентні. В цьому випадку, довжина сторони, протилежної куту, буде більшою, ніж довжина прилеглої сторони. Якщо кут прямий, тоді приходимо до постулату ПГК, також третя сторона може бути обчислена через теорему Піфагора, і можна використати ССС постулат.
Якщо два трикутники задовольняють умові ССК і відповідні кути гострі, а довжина сторони, протилежної до кута, більша або дорівнює прилеглій стороні, тоді два трикутники конгруентні.
Якщо два трикутники задовольняють умові ССК і відповідні кути гострі, а довжина протилежної сторони дорівнює довжині прилеглої сторони, помноженій на синус відомого кута, тоді два трикутники конгруентні.
Якщо два трикутники задовольняють умові ССК і відповідні кути гострі, а довжина протилежної сторони більша за довжину прилеглої сторони, помноженої на синус відповідного кута, але менша за довжину прилеглої сторони, тоді два трикутники необов'язково конгруентні. Виникає двозначність, два різних трикутника можуть задовольняти цим умовам.
Кут-Кут-Кут[ред. | ред. код]
ККК (Кут-Кут-Кут) не надає інформації про розмір трикутників, тож доводить лише подібність, а не конгруентність в евклідовому просторі. Однак в сферичній геометрії та гіперболічній геометрії (де кут є функцією розміру) цього достатньо для конгруентності у викривленому просторі.[2]
Конгруентність багатокутників[ред. | ред. код]

Аби два багатокутники вважалися конгруентними, вони повинні мати однакову кількість сторін (і таким чином однакову кількість вершин). Два багатокутники із n сторонами будуть конгруентними тоді і тільки тоді, коли вони мають чисельно ідентичні послідовності (навіть якщо для одного багатокутника по годинниковій стрілці, і проти годинникової стрілки для іншого) сторона-кут-сторона-кут-… для всіх n сторін і n кутів.
Конгруентність багатокутників можна установити графічним способом наступним чином:
- По-перше, зіставте і позначте відповідні вершини двох фігур.
- По-друге, намалюйте вектор від вершин однієї фігури до відповідних вершин іншої фігури. Перемістіть першу фігуру за допомогою цього вектор таким чином, що ці дві вершини будуть збігатися.
- По-третє, поверніть переміщену фігуру довкола зіставленої вершини допоки пара відповідних сторін не буде збігатися.
- Четверте, зробіть відображення обернутої фігури відносно зіставленої сторони доки фігури не будуть збігатися.
Якщо у будь-який момент часу описані кроки не можливо виконати, дані багатокутники не є конгруентними.
Примітки[ред. | ред. код]
- ↑ Congruence. Math Open Reference. 2009. Архів оригіналу за 5 жовтня 2017. Процитовано 2 червня 2017.
- ↑ Cornel, Antonio (2002). Geometry for Secondary Schools. Mathematics Textbooks Second Edition. Bookmark Inc. ISBN 971-569-441-1.
Посилання[ред. | ред. код]
- ССС(англ.)
- ССК [Архівовано 1 грудня 2008 у Wayback Machine.](англ.)
- Інтерактивна анімація демонструє Конгруентні кути [Архівовано 8 липня 2008 у Wayback Machine.], Конгруентні відрізки [Архівовано 20 липня 2008 у Wayback Machine.], Конгруентні трикутники [Архівовано 4 липня 2008 у Wayback Machine.], Конгруентні багатокутники [Архівовано 20 липня 2008 у Wayback Machine.](англ.)
