Теорема Піфагора


Теоре́ма Піфаго́ра (Пітаго́ра[1]) — одна із засадничих теорем евклідової геометрії, яка встановлює співвідношення між сторонами прямокутного трикутника. Уважається, що її довів грецький математик Піфагор, на чию честь її й названо (є й інші версії, зокрема думка, що цю теорему в загальному вигляді було сформульовано математиком-піфагорійцем Гіппасом).
Теорема[ред. | ред. код]
Теорема звучить так:
|
Позначивши довжину гіпотенузи трикутника як , а довжини катетів як та , отримаємо такі формули:
- ,
- .
Отже, теорема Піфагора встановлює співвідношення, яке дає змогу визначити довжину сторони прямокутного трикутника, знаючи довжини двох інших. Відповідно, в алгебраїчній інтерпретації теорему можна сформулювати так:
|
Теорема Піфагора є окремим випадком теореми косинусів, яка визначає співвідношення між сторонами довільного трикутника.
Доведено також зворотне твердження (називають також зворотною до теореми Піфагора):
|
Історія[ред. | ред. код]

Історію теореми можна розділити на чотири частини: знання про Піфагорові числа, знання про відношення сторін у прямокутному трикутнику, знання про відношення суміжних кутів і доведення теореми.
Мегалітичні споруди близько 2500 до н. е. в Єгипті та Північній Європі містять прямокутні трикутники зі сторонами з цілих чисел.[2] Бартель ван дер Варден висловив гіпотезу, що в ті часи Піфагорові числа були знайдені алгебраїчно.[3]
Написаний між 2000 та 1876 до н. е. папірус часів Середнього Єгипетського царства Berlin 6619 містить задачу, розв'язком якої є числа Піфагора.
Написана під час правління Хамурапі Великого (між 1790 і 1750 до н.е) вавилонська табличка Plimpton 322 містить багато записів, тісно пов'язаних з числами Піфагора.
У сутрах Будхаяни[en], які датуються за різними версіями 8-им чи 2-им століттям до н. е. в Індії, містяться Піфагорові числа, виведені алгебраїчно, формулювання теореми Піфагора та геометричне доведення для рівнобедреного прямокутного трикутника.
У сутрах Апастамби (близько 600 до н. е.) міститься числове доведення теореми Піфагора з використанням обчислення площі. Ван дер Варден уважає, що воно було засноване на традиціях попередників. Згідно з Альбертом Бурком, це оригінальне доведення теореми, і він припускає, що Піфагор відвідав Араконам і скопіював його.
Піфагор, роки життя якого зазвичай приймають за 569 — 475 до н. е., використовує алгебраїчні методи розрахунку піфагорових трійок, згідно з Прокловими коментарями до Евкліда. Прокл, однак, жив між 410 і 485 роками н. е. Згідно з Томасом Гізом, немає ніяких вказівок на авторство теореми протягом п'яти століть після Піфагора. Однак такі автори, як Плутарх або Цицерон, приписали теорему Піфагору у такий спосіб, ніби авторство було широко відоме і безсумнівне.[4]
Близько 400 до н. е. згідно з Проклом, Платон дав метод розрахунку піфагорових трійок, що поєднував алгебру та геометрію. Близько 300 до н. е., в «Началах» Евкліда маємо найдавніше аксіоматичне доведення, яке збереглося до наших днів.
Написана десь між 500 до н. е. і 200 до н. е., китайська математична книга «Чу Пей» (кит. 周髀算经) дає візуальне доведення теореми Піфагора, яка в Китаї називається теорема Гугу (кит. 勾股定理), для трикутника із сторонами (3, 4, 5). Під час правління династії Хань, з 202 до н. е. до 220 н. е. Піфагорові трійки з'являються в книзі «Математика в дев'яти книгах» разом із згадкою про прямокутні трикутники.[5]
Вперше зафіксовано використання теореми в Китаї, де вона відома як теорема Гугу (кит. 勾股定理), та в Індії, де вона відома як теорема Баскара.
Багато дискутується, чи була теорема Піфагора відкрита один раз чи багато разів. Боєр (1991 р.) уважає, що знання, виявлені в Шульба Сутрах, можуть бути месопотамського походження.[6]
Доведення[ред. | ред. код]
Алгебраїчне доведення[ред. | ред. код]

Відомо понад сто доведень теореми Піфагора.
Тут представлено доведення, засноване на теоремі існування площі фігури:
- Розташуємо чотири однакові прямокутні трикутники так, як це зображено на рисунку.
- Чотирикутник зі сторонами є квадратом, оскільки сума двох гострих кутів , а розгорнутий кут — .
- Площа всієї фігури рівна, з одної сторони, площі квадрата зі стороною , а з іншої — сумі площ чотирьох трикутників і внутрішнього квадрата.
- ;
- ;
- ;
За подібністю трикутників[ред. | ред. код]

Нехай — прямокутний трикутник, в якому кут прямий, як показано на рисунку. Проведемо висоту з точки і назвемо точку перетину зі стороною . Утворений трикутник подібний до трикутника , оскільки вони обидва прямокутні (за визначенням висоти) і в них спільний кут , очевидно, третій кут буде в цих трикутників також однаковий. Аналогічно, трикутник також подібний до трикутника . З подібності трикутників: Якщо
- ,
тоді
- та .
Це можна записати у вигляді
- та .
Якщо додати ці дві рівності, отримаємо
- .
Іншими словами, теорема Піфагора:
- .
Доведення Евкліда[ред. | ред. код]

В Евклідових «Началах» теорема Піфагора доведена методом паралелограмів. Нехай , , — вершини прямокутного трикутника з прямим кутом . Опустимо перпендикуляр з точки на сторону, протилежну до гіпотенузи в квадраті, побудованому на ній. Лінія ділить квадрат на два прямокутники, кожен з яких має таку саму площу, що й квадрати, побудовані на катетах. Головна ідея при доведенні полягає в тому, що верхні квадрати перетворюються на паралелограми такої самої площі, а тоді повертаються і перетворюються на прямокутники в нижньому квадраті і знову при незмінній площі.
Для формального доведення нам необхідні чотири елементарні леми:
- Якщо дві сторони одного трикутника і кут між ними дорівнюють відповідно двом сторонам та куту між ним іншого трикутника, то такі трикутники рівні (сторона-кут-сторона).
- Площа трикутника дорівнює половині площі паралелограма, що має таку саму основу і таку саму висоту.
- Площа прямокутника дорівнює добутку двох суміжних сторін.
- Площа квадрата дорівнює добутку двох його сторін (випливає з третьої леми).
Тоді кожен верхній квадрат пов'язаний з трикутником, конгруентним з іншим трикутником, який пов'язаний поворотом з одним із двох прямокутників, що утворюють нижній квадрат.[7]
Перейдемо до доведення:
- Нехай — прямокутний трикутник з прямим кутом .
- На кожній стороні , , і побудуємо квадрати , та в такому ж порядку. Побудова квадратів тут же вимагає попередньої теореми Евкліда і залежить від постулату паралельності.[8]
- З точки проводимо пряму, паралельну до і . Вона перпендикулярно перетне відрізки та в точках та , відповідно.
- Проведемо відрізки і , отримаємо трикутники і .
- Кути і — прямі; відповідно точки , і — колінеарні. Так само , і .
- Кути і — обидва прямі; тоді кут дорівнює куту , оскільки обидва є сумою прямого кута та кута .
- Трикутники та рівні за двома сторонами та кутом між ними.
- Оскільки точки , і — колінеарні, площа прямокутника дорівнює двом площам трикутника ().
- Аналогічно міркуючи, отримаємо .
- З одного боку, площа дорівнює сумі площ прямокутників та , а з іншого боку, це площа квадрата , або .
«Піфагорові штани» — жартівлива назва цього доказу.[джерело?]
Використовуючи диференціали[ред. | ред. код]

До теореми Піфагора можна прийти розглядом залежності величини гіпотенузи від приросту сторони (див. малюнок праворуч), застосувавши невелике обчислення.
У результаті приросту сторони з подібних трикутників для нескінченно малих приростів:
- .
Застосуємо розділення змінних.
Інтегруючи, отримаємо:
- .
Якщо тоді , тож «константа» — . Тоді
- .
Як можна побачити, квадрати отримано завдяки пропорції між приростами та сторонами, тоді як сума є результатом незалежного внеску приростів сторін, що не очевидно з геометричних доведень. У цих рівняннях і , відповідно, — нескінченно малі прирости сторін і . Але замість них ми використовуємо і , тоді границя їхнього відношення, якщо вони прямують до нуля, дорівнює (похідній) і також дорівнює (відношенню довжин сторін трикутників), в результаті чого отримуємо диференціальне рівняння.
Застосування і наслідки теореми[ред. | ред. код]
Піфагорові трійки[ред. | ред. код]
Піфагорові трійки — це три натуральні числа , та такі, що виконується рівність . Іншими словами, Піфагорові трійки — це сторони прямокутного трикутника, якщо всі вони є цілими. На мегалітичних спорудах в північній Європі є свідчення, що відомості про такі трійки були відомі до винайдення писемності. Такі трійки зазвичай записують у вигляді Деякі найвідоміші приклади: (3, 4, 5) та (5, 12, 13).
Примітивними Піфагоровими числами називають такі , та , які є взаємно простими (найбільший спільний дільник , та дорівнює 1)
Нижче наведено перелік примітивних Піфагорових чисел менших від 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97).
- Найкраще запам'ятовуються такі Піфагорові числа (менші від 100):
- (3, 4, 5), (6, 8, 10), (9, 12, 15), (12, 16, 20), (15, 20, 25), (18, 24, 30), (21, 28, 35), (24, 32, 40), (27, 36, 45), (30, 40, 50), (33, 44, 55), (36, 48, 60), (39, 52, 65), (42, 56, 70), (45, 60, 75), (48, 64, 80), (51, 68, 85), (54, 72, 90), (57, 76, 95), (60, 80, 100).
- Ці трійки утворюються множенням першої трійки чисел (3, 4, 5) на числа 2, 3, 4, 5 тощо.
Неспівмірні довжини[ред. | ред. код]

Одним з наслідків теореми Піфагора є те, що відрізки на лінії, довжина яких є неспівмірною (тобто, співвідношення між якими дає ірраціональне число), можуть бути побудовані за допомогою лінійки та циркуля. Теорема Піфагора дає змогу побудувати неспівмірні довжини через те, що гіпотенуза трикутника пов'язана з його сторонам через корінь квадратний.
Малюнок справа демонструє, як побудувати відрізки, довжина яких у співвідношенні дає корінь квадратний будь-якого цілого числа. Кожен трикутник має сторону (позначену «1»), довжина якої є вибрана одиниця вимірювання. На кожному прямокутному трикутнику завдяки теоремі Піфагора отримуємо довжину гіпотенузи, виражену у вибраних одиницях. Якщо гіпотенуза пов'язана з одиницею вимірювання через квадратний корінь з додатним цілим числом, що не є піднесенням до квадрата, тоді ми отримуємо реалізацію неспівмірності для цієї одиниці. Наприклад, , , .
Неспівмірні величини конфліктують з концепцією школи Піфагора про те, що всі числа є цілими. Школа Піфагора давала собі раду з дробами, порівнюючи кратні числа, які мали спільний дільник.[9] Згідно з однією легендою, Гіппаса з Метапонту (близько 470 до н. е.) втопили в морі через те, що він розказував про існування ірраціональних чи неспівмірних величин.[10][11]
Евклідова відстань у різних координатних системах[ред. | ред. код]

Формулу відстані між точками в декартовій системі координат отримуємо з теореми Піфагора.[12] Якщо маємо точки на площині і , то відстань між ними, яка також називається Евклідова відстань, можна обчислити так:
- .
Або, узагальнюючи для n-вимірного Евклідового простору, для відстані між двома точками та можна сформулювати загальніший випадок теореми Піфагора:
Якщо не можна використати Декартові координати, наприклад, у випадку полярних координат, або в загальнішому випадку, якщо треба використати криволінійні координати, формули для розрахунку Евклідової відстані складніші, ніж теорема Піфагора, але можуть бути виведені з її допомогою. Типовий приклад, коли формула відстані між двома точками приведена до криволінійних координат, можна побачити при застосуванні полінома Лежандра у фізиці. Ці формули можна знайти, використовуючи Теорему Піфагора разом із формулами зв'язку криволінійних координат з декартовими. Наприклад, полярні координати можна записати так:
- .
Тоді відстань між двома точками та дорівнює
- .
Якщо піднести до степеня й об'єднати змінні, отримаємо формулу для визначення відстані між точками у полярних координатах:
- ,
використовуючи формули перетворення добутків функцій. Цю формулу, що є теоремою косинусів, іноді називають узагальненою теоремою Піфагора.[13]
Якщо результатну формулу використати для випадку, коли радіуси знаходяться під прямим кутом, кут між ними дорівнює , тоді знову отримаємо теорему Піфагора: . Теорема Піфагора справедлива для прямокутних трикутників, проте є частковим випадком загальнішої теореми косинусів, яка справедлива для будь-якого трикутника.
Тригонометрична тотожність Піфагора[ред. | ред. код]
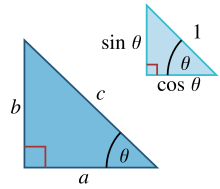
Для прямокутного трикутника із сторонами a, b та гіпотенузою c, запишемо тригонометричні визначення синуса і косинуса кута між стороною та гіпотенузою:
- ,
звідси випливає, що
- ,
де в останньому кроці доведення застосовуємо теорему Піфагора. Цю залежність між синусом і косинусом іноді називають фундаментальною тригонометричною тотожністю Піфагора.[14] У подібних трикутників, співвідношення між сторонами рівне незалежно від розмірів трикутника, а залежить тільки від кутів. Відповідно, на рисунку зображено трикутник з гіпотенузою, яка дорівнює одиниці, сторона протилежна до кута дорівнює і прилегла сторона — в одиницях гіпотенузи.
Узагальнення[ред. | ред. код]
Подібні геометричні фігури на трьох сторонах[ред. | ред. код]

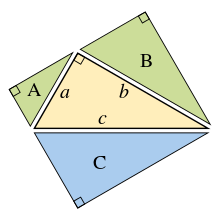
Узагальнення теореми Піфагора робив Евклід у своїй праці «Начала», розширивши площі квадратів на сторонах до площ подібних геометричних фігур:[15]
Якщо побудувати подібні геометричні фігури (див. Евклідова геометрія) на сторонах прямокутного трикутника, тоді сума двох менших фігур буде дорівнювати площі більшої фігури.
Головна ідея цього узагальнення полягає в тому, що площа подібної геометричної фігури пропорційна до квадрата будь-якого свого лінійного розміру і зокрема до квадрата довжини будь-якої сторони. Отже, для подібних фігур з площами A, B і C, що побудовані на сторонах з довжиною , і , маємо
- ,
- .
Але, за теоремою Піфагора, , тоді A + B = C.
І навпаки, якщо ми зможемо довести, що для трьох подібних геометричних фігур без використання теореми Піфагора, тоді ми зможемо довести саму теорему, рухаючись у зворотному напрямку. Наприклад, стартовий центральний трикутник може бути повторно використаний як трикутник на гіпотенузі, і два подібні прямокутні трикутники ( і ), побудовані на двох інших сторонах, які утворюються в результаті поділу центрального трикутника його висотою. Сума площ двох менших трикутників тоді очевидно дорівнює площі третього, отже, і, виконуючи попереднє доведення в зворотному порядку, отримаємо теорему Піфагора .
Теорема косинусів[ред. | ред. код]
Теорема Піфагора — це окремий випадок загальнішої теореми косинусів, яка пов'язує довжини сторін в довільному трикутнику:[16]
- ,
де — кут між сторонами і .
Якщо дорівнює , то і формула спрощується до звичайної теореми Піфагора.
Довільний трикутник[ред. | ред. код]

Для вибраного кута довільного трикутника із сторонами , , впишемо рівнобедрений трикутник так, щоб рівні кути при його основі дорівнювали вибраному куту. Припустимо, що вибраний кут протилежний до сторони позначеної . Унаслідок ми отримали трикутник ABD з кутом , що протилежний стороні та стороною . Другий трикутник утворюється кутом , що протилежний до сторони та стороною з довжиною , як показано на рисунку. Сабіт ібн Курра[18] стверджував, що сторони в цих трьох трикутниках пов'язані так:[19][20]
- .
Коли кут наближається до , основа рівнобедреного трикутника зменшується і дві сторони і перекривають одна одну все менше і менше. Коли , ADB перетворюється в прямокутний трикутник, , і отримуємо початкову теорему Піфагора.
Розглянемо одне з доведень. Трикутник має такі самі кути, як і трикутник , але в зворотному порядку. Два трикутники мають спільний кут у вершині , обидва мають кут і також мають однаковий третій кут, за сумою кутів трикутника. Відповідно, — подібний до відображення трикутника , як зображено на нижньому рисунку. Запишемо співвідношення між сторонами протилежними і прилеглими до кута ,
- .
Так само відображення іншого трикутника,
- .
Перемножимо дроби та додамо ці два співвідношення:
- ,
що і треба було довести.
Довільні трикутники через паралелограми[ред. | ред. код]
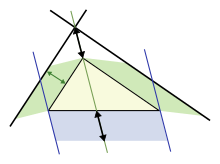
зелена площа дорівнює синій площі

Зробимо подальше узагальнення для не прямокутних трикутників, використовуючи паралелограми на трьох сторонах замість квадратів.[21] (а квадрати — це звичайно частковий випадок.) Верхній рисунок демонструє, що для гострокутного трикутника, площа паралелограма на довшій стороні дорівнює сумі паралелограмів на двох інших сторонах, за умови що паралелограм на довгій стороні побудовано як зображено на рисунку(розміри відзначені стрілками однакові і визначають сторони нижнього паралелограма). Ця заміна квадратів паралелограмами несе чітку схожість з початковою теоремою Піфагора, вважається, що це сформулював Папп з Александрії в 4 р. н. е.[21]
Нижній рисунок показує хід доведення. Подивимось на ліву сторону трикутника. Лівий зелений паралелограм має таку саму площу, як ліва частина синього паралелограма, тому що вони мають таку саму основу і висоту . Крім того, лівий зелений паралелограм має таку саму площу, як лівий зелений паралелограм на верхньому рисунку, тому що вони мають таку саму основу (верхня ліва сторона трикутника) і таку саму висоту перпендикулярну до цієї сторони трикутника. Аналогічно розмірковуючи для правої сторони трикутника, доведемо, що нижній паралелограм має таку саму площу, як два зелені паралелограми.
Комплексні числа[ред. | ред. код]
Формулу Піфагора використовують, щоб знайти відстань між двома точками в декартовій координатній системі і ця формула справедлива для всіх дійсних координат: відстань між двома точками і дорівнює
- .
Не виникає проблем з формулою, якщо до комплексних чисел ставитись як до векторів з дійсними компонентами . Відстань між комплексними числами та представляється у формі теореми Піфагора[22]:
- .
Наприклад, відстань s між та розраховуємо як модуль вектора , або
- .
Однак, для операцій з векторами з комплексними координатами необхідно провести певне вдосконалення формули Піфагора. Відстань між точками з комплексними координатами і , , і всі комплексні, сформулюємо використовуючи абсолютні величини. Відстань заснована на векторній різниці в такому вигляді:[23] нехай різниця , де — дійсна частина різниці, — уявна частина, де . Аналогічно, нехай . Тоді:
- ,
де — це комплексне спряжене число для . Наприклад, відстань між точками та , розрахуємо різницю і в результаті ми б отримали , якби не були використані комплексні спряжені. Отже, використовуючи вдосконалену формулу, отримаємо
- .
Модуль визначений так:
- ,
це є Ермітів скалярний добуток.[22]
Стереометрія[ред. | ред. код]
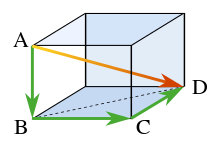
Теорема Піфагора може бути застосована для стереометрії в такому вигляді. Розглянемо прямокутний паралелепіпед, як показано на рисунку. Знайдемо довжину діагоналі за теоремою Піфагора:
де три сторони утворюють прямокутний трикутник. Використаємо горизонтальну діагональ і вертикальне ребро , щоб знайти довжину діагоналі , для цього знову використаємо теорему Піфагора:
або, якщо все записати одним рівнянням:
Цей результат — це тривимірний вираз для визначення величини вектора (діагональ ) виражений через його перпендикулярні складові (три взаємно перпендикулярні сторони):
- .
Це рівняння можна розглядати як узагальнення теореми Піфагора для багатовимірного простору. Проте, результат насправді просто кількаразове застосування теореми Піфагора до послідовності прямокутних трикутників у послідовно перпендикулярних площинах.
Значним узагальненням теореми Піфагора для тривимірного простору є теорема де Гуа, названа на честь Жана Поля де Гуа: якщо тетраедр має прямий кут (як у куба), тоді квадрат площі грані протилежної до прямого кута дорівнює сумі квадратів площ інших трьох граней. Цей висновок може бути узагальнений для «n-вимірної теореми Піфагора»:[24]
Векторний простір[ред. | ред. код]
У випадку ортогональної системи векторів має місце рівність, яку теж називають теоремою Піфагора:
- .
Якщо — це проєкції вектора на координатні осі, то ця формула збігається з відстанню Евкліда — і означає, що довжина вектора рівна кореню квадратному суми квадратів його компонентів.
Аналог цієї рівності у випадку нескінченної системи векторів має назву рівності Парсеваля.
Неевклідова геометрія[ред. | ред. код]
Теорема Піфагора виводиться з аксіом евклідової геометрії і, фактично, не справджується для неевклідової геометрії, в тому вигляді, в якому записана вище.[25] (Тобто теорема Піфагора виявляється своєрідним еквівалентом до аксіоми паралельності Евкліда).[26][27] Іншими словами, в неевклідовій геометрії співвідношення між сторонами трикутника обов'язково буде у формі відмінній від Піфагора. Наприклад, в сферичній геометрії всі три сторони прямокутного трикутника (скажімо , і ), що обмежує собою октант (восьму частину) одиничної сфери мають довжину , що суперечить теоремі Піфагора, тому що .
Розглянемо тут два випадки неевклідової геометрії — сферична і гіперболічна геометрії; в обох випадках, як і для евклідового простору, для не прямокутних трикутників, результат, що замінює теорему Піфагора, випливає з теореми косинусів.
Проте, теорема Піфагора залишається справедливою для гіперболічної та еліптичної геометрії, якщо вимогу про прямокутність трикутника замінити умовою, що сума двох кутів трикутника має дорівнювати третьому, скажімо . Тоді співвідношення між сторонами виглядає так: сума площ кіл з діаметрами і дорівнює площі кола з діаметром .[28]
Сферична геометрія[ред. | ред. код]

Для будь-якого прямокутного трикутника на сфері радіусом (наприклад, якщо кут γ в трикутнику прямий) із сторонами , , співвідношення між сторонами буде мати такий вигляд:[29]
- .
Ця рівність може бути виведена як особливий випадок сферичної теореми косинусів, яка справедлива для всіх сферичних трикутників:
- .
Застосуємо ряд Тейлора до функції косинуса , можна показати, що якщо радіус наближається до нескінченості, а аргументи , і наближаються до нуля, сферичне співвідношення між сторонами в прямокутному трикутнику наближається до теореми Піфагора. Підставимо наближені значення для кожного косинуса:
- ,
де — доданки вищого порядку, якими можна знехтувати при великих значеннях .
Перемножимо вирази в дужках, отримаємо теорему Піфагора для великих радіусів :
- .
Гіперболічна геометрія[ред. | ред. код]

Для прямокутного трикутника в гіперболічній геометрії із сторонами , , , якщо сторона протилежна до прямого кута, співвідношення між сторонами буде таке:[30]
- ,
де — це гіперболічний косинус. Ця формула є частковим випадком гіперболічної теореми косинусів, яка справедлива для всіх трикутників:[31]
- ,
де — це кут, вершина якого протилежна до сторони .
Використаємо ряди Тейлора для гіперболічного косинуса , можна довести що, якщо гіперболічний трикутник зменшується (тобто, коли , і наближаються до нуля), то гіперболічні співвідношення в прямокутному трикутнику наближаються до теореми Піфагора.
Диференціальна геометрія[ред. | ред. код]

У тривимірному просторі для двох точок, що віддалені одна від одної на нескінченно малу віддаль запишемо теорему Піфагора:
- ,
де — це відстань між точками, а (, , ) — компоненти вектора, що з'єднує ці дві точки. Такий простір називається евклідовим. Проте, узагальнення цього виразу придатне для загальних координат (не тільки Декартових) і загальних просторів (не тільки Евклідових) має вигляд:[32]
- ,
де gij називається метричним тензором. Це може бути функція позиції. Такі криволінійні простори включають Ріманову геометрію як загальний приклад. Це формулювання також підходить для Евклідового простору при застосуванні криволінійних координат. Наприклад, для полярних координат:
- .
Векторний добуток[ред. | ред. код]

Теорема Піфагора пов'язує два вирази величини векторного добутку.
Один з підходів до визначення векторного добутку вимагає, щоб він задовольняв рівняння:[33]
- .
У цій формулі використовується скалярний добуток. Права сторона рівняння називається детермінант Грама для і , що дорівнює площі паралелограма утвореного цими двома векторами. Виходячи з цієї вимоги, а також вимоги про перпендикулярність векторного добутку до його складових і випливає що, за винятком тривіальних випадків з 0 та 1-вимірного простору, векторний добуток визначений тільки в трьох та семи вимірах.[34] Використаємо визначення кута в n-вимірному просторі:[35]
- ,
ця властивість векторного добутку дає його величину в такому вигляді:
- .
Через фундаментальну тригонометричну тотожність Піфагора[14] отримуємо іншу форму запису його величини:
- .
Альтернативний підхід до визначення векторного добутку використовує вираз для його величини. Тоді, міркуючи у зворотному порядку, отримуємо зв'язок із скалярним добутком:
- .
Див. також[ред. | ред. код]
- Числа Піфагора
- Прямокутний трикутник
- Тригонометрична тотожність Піфагора
- Теорема косинусів
- Трикутник
Примітки[ред. | ред. код]
- ↑ § 123. Буквосполучення th у словах грецького походження. Український правопис 2019 року (PDF) (укр.). 2019. Архів оригіналу (PDF) за 17 вересня 2019. Процитовано 21 січня 2021.
- ↑ Megalithic Monuments. Архів оригіналу за 21 червня 2013. Процитовано 29 жовтня 2008.
- ↑ Van der Waerden 1983.
- ↑ Heath, Vol I, p. 144
- ↑ Swetz
- ↑ Boyer (1991). «China and India»
- ↑ See for example Mike May S.J., Pythagorean theorem by shear mapping [Архівовано 14 жовтня 2016 у Wayback Machine.], Saint Louis University website Java applet
- ↑ Jan Gullberg (1997). Mathematics: from the birth of numbers. W. W. Norton & Company. с. 435. ISBN 039304002X. Архів оригіналу за 3 липня 2014. Процитовано 1 квітня 2011.
- ↑ Shaughan Lavine (1994). Understanding the infinite. Harvard University Press. с. 13. ISBN 0674920961. Архів оригіналу за 28 березня 2016. Процитовано 1 квітня 2011.
- ↑ Heath 1921, Vol I, pp. 65; Див. James R. Choike (1980). The pentagram and the discovery of an irrational number. The College Mathematics Journal. 11: 312—316.
- ↑ A careful discussion of Hippasus' contributions is found in Kurt Von Fritz (Apr., 1945). The Discovery of Incommensurability by Hippasus of Metapontum. The Annals of Mathematics, Second Series. Annals of Mathematics. 46 (2): 242—264. JSTOR 1969021.
- ↑ Jon Orwant, Jarkko Hietaniemi, John Macdonald (1999). Euclidean distance. Mastering algorithms with Perl. O'Reilly Media, Inc. с. 426. ISBN 1565923987. Архів оригіналу за 28 березня 2016. Процитовано 2 квітня 2011.
- ↑ Wentworth, George (2009). Plane Trigonometry and Tables. BiblioBazaar, LLC. с. 116. ISBN 1-103-07998-0., Exercises, page 116 [Архівовано 28 березня 2016 у Wayback Machine.]
- ↑ а б Lawrence S. Leff (2005). PreCalculus the Easy Way (вид. 7th). Barron's Educational Series. с. 296. ISBN 0764128922.
- ↑ Euclid's Elements: Book VI, Proposition VI 31: «In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle.»
- ↑ Lawrence S. Leff (1 травня 2005). cited work. Barron's Educational Series. с. 326. ISBN 0764128922.
- ↑ Howard Whitley Eves (1983). §4.8:...generalization of Pythagorean theorem. Great moments in mathematics (before 1650). Mathematical Association of America. с. 41. ISBN 0883853108. Архів оригіналу за 8 липня 2014. Процитовано 14 квітня 2011.
- ↑ Tâbit ibn Qorra (full name Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826—901 AD) was a physician living in Baghdad who wrote extensively on Euclid's Elements and other mathematical subjects.
- ↑ Aydin Sayili (Mar. 1960). Thâbit ibn Qurra's Generalization of the Pythagorean Theorem. Isis. 51 (1): 35—37. doi:10.1086/348837. JSTOR 227603.
- ↑ Judith D. Sally, Paul Sally (21 грудня 2007). Exercise 2.10 (ii). Cited work. с. 62. ISBN 0821844032. Архів оригіналу за 28 квітня 2015. Процитовано 14 квітня 2011.
- ↑ а б For the details of such a construction, see George Jennings (1997). Figure 1.32: The generalized Pythagorean theorem. Modern geometry with applications: with 150 figures (вид. 3rd). Springer. с. 23. ISBN 038794222X.
- ↑ а б Alfred Gray, Elsa Abbena, Simon Salamon (2006). Modern differential geometry of curves and surfaces with Mathematica (вид. 3rd). CRC Press. с. 194. ISBN 1584884487.
- ↑ Arlen Brown, Carl M. Pearcy (1995). Item C: Norm for an arbitrary n-tuple.... An introduction to analysis. Springer. с. 124. ISBN 0387943692. Архів оригіналу за 28 квітня 2015. Процитовано 14 квітня 2011. See also pages 47-50.
- ↑ Rajendra Bhatia (1997). Matrix analysis. Springer. с. 21. ISBN 0387948465.
- ↑ Stephen W. Hawking (2005). cited work. с. 4. ISBN 0762419229. Архів оригіналу за 2 вересня 2020. Процитовано 15 квітня 2011.
- ↑ Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (вид. 2nd). с. 2147. ISBN 1584883472. Архів оригіналу за 18 серпня 2020. Процитовано 15 квітня 2011.
The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
- ↑ Alexander R. Pruss (2006). The principle of sufficient reason: a reassessment. Cambridge University Press. с. 11. ISBN 052185959X. Архів оригіналу за 25 вересня 2020. Процитовано 15 квітня 2011.
We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.
- ↑ Victor Pambuccian (December 2010). Maria Teresa Calapso's Hyperbolic Pythagorean Theorem. The Mathematical Intelligencer. 32 (4): 2. doi:10.1007/s00283-010-9169-0.
- ↑ Barrett O'Neill (2006). Exercise 4. Elementary differential geometry (вид. 2nd). Academic Press. с. 441. ISBN 0120887355.
- ↑ Saul Stahl (1993). Theorem 8.3. The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. с. 122. ISBN 086720298X.
- ↑ Jane Gilman (1995). Hyperbolic triangles. Two-generator discrete subgroups of PSL(2,R). American Mathematical Society Bookstore. ISBN 0821803611.
- ↑ Tai L. Chow (2000). Mathematical methods for physicists: a concise introduction. Cambridge University Press. с. 52. ISBN 0521655447.
- ↑ WS Massey (Dec. 1983). Cross products of vectors in higher dimensional Euclidean spaces. The American Mathematical Monthly. Mathematical Association of America. 90 (10): 697—701. doi:10.2307/2323537. JSTOR 2323537.
- ↑ Although a cross-product involving n − 1 vectors can be found in n dimensions, a cross-product involving only two vectors can be found only in 3 dimensions and in 7 dimensions. See Pertti Lounesto (2001). §7.4 Cross product of two vectors. Clifford algebras and spinors (вид. 2nd). Cambridge University Press. с. 96. ISBN 0521005515.
- ↑ Francis Begnaud Hildebrand (1992). Methods of applied mathematics (вид. Reprint of Prentice-Hall 1965 2nd). Courier Dover Publications. с. 24. ISBN 0486670023.
Література[ред. | ред. код]
- Heath, Sir Thomas, A History of Greek Mathematics (2 Vols.), Clarendon Press, Oxford (1921), Dover Publications, Inc. (1981), ISBN 0-486-24073-8.
- Swetz, Frank, Kao, T. I., Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China, Pennsylvania State University Press. 1977.
- Van der Waerden, B.L., Geometry and Algebra in Ancient Civilizations, Springer, 1983.
- Euclid (1956). The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary [Архівовано 27 жовтня 2020 у Wayback Machine.]. Vol. 1 (Books I and II).
- Neugebauer, Otto (1969). The exact sciences in antiquity [Архівовано 2 листопада 2013 у Wayback Machine.]. Acta Historica Scientiarum Naturalium et Medicinalium. 9 (Republication of 1957 Brown University Press 2nd ed.). Courier Dover Publications. pp. 1–191 ISBN 0-486-22332-9. PMID 14884919.
- Еленьский Щ. По следам Пифагора. М., 1961
- Ван-дер-Варден Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. М., 1959
- В. Литцман, «Теорема Пифагора» [Архівовано 27 січня 2010 у Wayback Machine.] М., 1960.
- Теорема Пифагора и пифагоровы тройки [Архівовано 3 березня 2016 у Wayback Machine.] глава из книги Д. В. Аносова «Взгляд на математику и нечто из нее»
Посилання[ред. | ред. код]
| Вікісховище має мультимедійні дані за темою: Теорема Піфагора |
- Теорема Піфагора [Архівовано 25 серпня 2012 у Wayback Machine.] (більш ніж 70 доведень від cut-the-knot) (англ.)
- Weisstein, Eric W. Теорема Піфагора(англ.) на сайті Wolfram MathWorld.
- https://mathshistory.st-andrews.ac.uk/HistTopics/Babylonian_Pythagoras/ [Архівовано 20 жовтня 2020 у Wayback Machine.]
- Інтерактивні посилання:
- Інтерактивне доведення [Архівовано 12 липня 2012 у Wayback Machine.] Теореми Піфагора за допомогою Java(англ.)
- Ще одне інтерактивне доведення [Архівовано 26 серпня 2012 у Wayback Machine.] Теореми Піфагора за допомогою Java(англ.)
- Теорема Піфагора [Архівовано 27 жовтня 2020 у Wayback Machine.] з інтерактивною анімацією(англ.)
- Pythagorean theorem water demo на YouTube
|
| |||||||||||||||||||||||
|
|
Ця стаття належить до добрих статей української Вікіпедії. |






















































































































































![{\displaystyle 1-\left({\frac {c}{R}}\right)^{2}=\left[1-\left({\frac {a}{R}}\right)^{2}\right]\left[1-\left({\frac {b}{R}}\right)^{2}\right]+\ \mathrm {higher\ order\ terms} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1ef24d3a2f47a0a87e2d2194ab588d694fa0493)






















